跨坐式单轨车导向轮稳定轮预压力研究*
张建全,黄运华,李 芾,陶功安
(1 株洲电力机车有限公司,湖南株洲412001;2 西南交通大学 机械工程学院,四川成都610031)
1991年重庆市政府正式批准轨道交通系统列入重庆市城市建设总体规划,并成立重庆市轨道交通总公司。轨道交通线路中,校场口至新山村线为高架单轨线,也是我国第一条单轨交通线[2]。此外,杭州市、东莞和石家庄市也均对单轨交通系统对本市轨道交通线路的适应性进行了研究[1]。单轨交通作为一种城市公共交通系统已经在我国受到越来越多的关注,但对于单轨车辆动力学方面的研究相对较少。本文即对影响单轨车辆动力学性能的导向轮、稳定轮的预压力进行研究,以期对单轨交通在我国的应用和发展有一定的指导意义。
1 单轨车转向架工作原理
与传统轨道交通相比,除供电方式、通信、信号系统等有所区别外,跨坐式单轨交通的最大区别主要反映在车辆转向架、轨道梁和道岔等3方面,称之为该交通系统的3大关键技术。跨坐式单轨车辆转向架是车辆的核心部件,是最能体现该交通系统运行特点的部分。转向架采用跨坐式无摇枕转向架、中心销牵引。每个转向架有4个走行轮、4个导向轮、2个稳定轮,都使用橡胶轮胎(如图1所示)[2,3]。走行轮采用充氮气无内胎钢丝橡胶轮胎,以轨道梁的上表面为走行面,起承载、传递牵引力、制动力和缓冲车辆竖向振动的作用;导向轮、稳定轮内充压缩空气,都以轨道梁的侧面为走行面,起到缓冲车辆横向振动的作用,其中导向轮在过弯道时起导向作用;稳定轮是在车辆受到离心力、风力的时候起稳定作用。为防止轮胎失气,每种车轮都备有辅助安全车轮。转向架构架由钢板焊接而成,其左右侧梁的前后有导向轮的支撑架,左右侧梁的中部有稳定轮的支撑架。车辆运行时,走行轮与稳定轮紧紧“抱”住轨道梁,其轨道梁不仅是承重的桥梁结构,同时也是支承和约束车辆行驶的轨道,承受较大的扭转荷载。
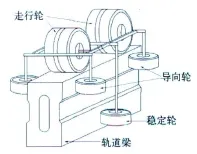
图1 跨坐式单轨车转向架原理图
2 车体的抗倾覆稳定性
车辆在横向力作用下,车体将产生横摆和侧滚,当外力消失后在悬挂装置的复原力和复原力矩的作用下,车体向平衡位置移动并引起自由振动,在各种阻力作用下,自由振动逐渐衰减并恢复到静平衡位置。车体离开平衡位置后,能自动恢复到平衡位置的特性称为车体在弹簧上具有抗倾覆稳定性[7]。如果车体离开平衡位置后不能自动恢复到平衡位置而继续保持倾斜状态,甚至逐渐增加倾斜而使车体倾覆,车体将在弹簧上丧失抗倾覆稳定性,出现这种现象是车辆安全运行所不允许的。在车辆设计中应确保车体在弹簧上有足够的抗倾覆稳定性。

式中Kpz为一系悬挂垂向刚度;Ksz为二系悬挂垂向刚度为车体质量;b1为一系悬挂横向跨距之半;b2为二系悬挂横向跨距之半。
为了确保车体在弹簧上有足够的抗倾覆稳定性,前苏联铁路规定车体浮心高度hm应大于车体重心高度hc的量在2 m以上[7],即:

由跨坐式单轨车辆的转向架结构原理图可以明显看到,单轨车辆走行轮的横向跨距很小,一般为400 mm,由公式(1)以及车辆相关参数可以得到单轨车空车的浮心高度只是比车体重心高50 mm左右,而在定员的情况下就远低于车体重心高度,所以单轨车辆很容易失稳,属“随遇不稳定”模式。因此,跨坐式转向架需要设置稳定轮,由此产生横向力从而形成反力矩来保证车辆的稳定性。跨坐式单轨车辆的导向是靠导向轮和轨道梁的压力来提供的,因此,导向轮和稳定轮与轨道梁之间的作用力对跨坐式单轨车辆的安全性、稳定性和平稳性有着重要的影响,本文即对导向轮和稳定轮与轨道梁之间的作用力进行深入研究[4-6,8]。
3 直线线路上车辆有无预压力时的仿真研究
利用多体动力学软件对跨坐式单轨车模型(参数见表1)其在定员情况下通过一带有激扰的直线路面进行仿真,仿真结果如图 2(a)~(e)所示。

表1 计算模型主要计算参数
图中各个字母的意义分别是B为导向轮稳定轮贴靠在轨道梁;C为稳定轮和轨道梁有一间隙,导向轮贴靠在轨道梁上;D为导向轮和轨道梁有一间隙,稳定轮贴靠在轨道梁上;E为导向轮、稳定轮和轨道梁均有一间隙;F为导向轮、稳定轮和轨道梁均有一预压力。
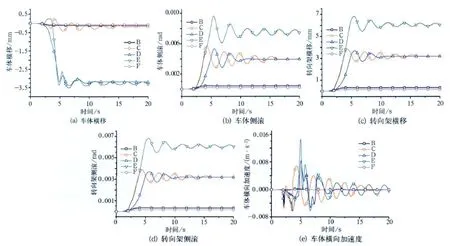
图2 单轨车通过一路面激励时动力学指标变化曲线
从图2的仿真结果可以看出:
(1)当导向轮稳定轮贴靠在轨道梁上(B),车辆在通过路面激扰后经过微小的振动后很快恢复到稳定状态,只是车体横移、车体侧滚、转向架横移、转向架侧滚均有一较小的偏移量。
(2)当导向轮贴靠在轨道梁上,而稳定轮有一间隙(C)的时候,车辆在通过路面激扰后要经过长时间的振动才能恢复到稳定状态,在稳定状态只有车体横移能够回到零位置附近,但仍有一较小的横移量,而车体侧滚、转向架横移、转向架侧滚均有一较大的偏移量。
(3)当导向轮与轨道梁有一间隙,而稳定轮贴靠在轨道梁(D)上的时候,车辆在通过路面激扰后很快产生一较大的偏移量,并经过一段时间的振动才能恢复到稳定状态。
(4)当导向轮和稳定轮同时和轨道梁有一间隙(E)的时候,车辆在通过路面激扰后很快产生一较大的偏移量,并经过长时间的振动才能恢复到稳定状态,只是车体横移较导向轮与轨道梁有一间隙,而稳定轮贴靠在轨道梁(D)上时稍大一点,而车体侧滚、转向架横移、转向架侧滚的偏移量则大了很多。
(5)当导向轮和稳定轮同时和轨道梁有一预压力(F)的时候,车辆在通过路面激扰后经过微小的振动后很快恢复到稳定状态,在稳定状态车辆基本回到零位置。
(6)从车体横向加速度图可以看到,当导向轮稳定轮贴靠在轨道梁上和有预压力的时候车体振动一两次就达到稳定,并且振幅很小;当有间隙存在时会有长时间的波动,并且幅值也比较大,尤其是导向轮和稳定轮同时存在间隙的时候波动最大。
由上述分析可知,导向轮、稳定轮与轨道梁之间的间隙加剧了车辆的振动和车辆的偏移量,使车辆的抗倾覆稳定性变差。当稳定轮和轨道梁有一间隙的时候会比导向轮和轨道梁之间有一间隙时的振动较大一些,是由于车辆的侧滚运动没有得到有效的抑制,当导向轮和稳定轮同时有一间隙的时候是最恶劣的情况,此时车辆的偏移量最大且振动最剧烈。当导向轮、稳定轮贴靠在轨道梁上和有一预压力的时候车体的偏移和振动情况会改善很多,其中有预压力的时候车辆的运行状态最好,此时车辆具有良好的抗倾覆稳定性。
4 曲线线路上导向轮稳定轮预压力研究
车辆在道路上运行时不可避免的要受到风力等其他外部激扰的影响,特别是在曲线通过时,由于存在离心力、重力的分力以及风力的作用,车体在曲线上会有较大的倾覆,此时导向轮稳定轮的预压力就显得尤为重要。
4.1 车辆圆曲线上横向受力分析
图3为车辆以一定速度通过圆曲线时横向的受力情况,从图中看出车辆在通过曲线时主要受到的横向力有导向轮、稳定轮的径向力、离心力和车辆重力在横向的分力、走行轮的侧向力。这些力在横向有以下关系:
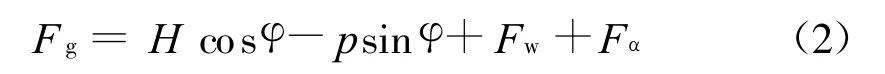
式中Fg为导向力;H为离心力;p为车辆重力;Fw为稳定轮抗倾覆力;Fα走行轮侧向力;φ为超高角。
从式(2)可以看出,这些力的变化是由车辆的运行速度、线路的超高以及曲线半径来决定的。
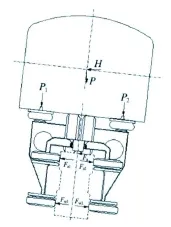
图3 车辆圆曲线上的受力图
4.2 有预压力时的曲线通过仿真
为了考察导向轮稳定轮预压力对车辆动力学性能的影响[4-6,8],仿真计算了单轨车辆在预压力从0 kN到15 kN变化时,通过100 m到500 m不同曲线半径超高率为7%的曲线时,车辆动力学性能指标的变化情况如图4(a)~(f)所示。
从图4可以看出,随着预压力的增加,导向轮稳定轮径向力的变化量、车体侧滚角、转向架侧滚角和车体横移量(车体相对于前后转向架中心的连线)显著变小后趋于平缓;随着曲线半径的增加,导向力变化量的减小比较明显,稳定轮径向力变化量、车体侧滚角、转向架侧滚角和车体横移略有减小;空气弹簧垂向力的变化随曲线半径和预压力的增加变化都比较小。
图5是导向轮稳定轮与轨道梁有5 kN预压力,跨坐式单轨车辆以均衡速度通过100 m半径7%超高率的曲线时,导向力和稳定轮径向力的变化随时间历程变化情况。
从图5可以看出,右侧导向轮和左侧稳定轮在缓和曲线上时就已经离开了轨道梁,在圆曲线上稳定轮径向力有长时间较小幅度的振荡。而此时若车辆受到外部激扰如强风的影响将给车辆带来危险,从而影响车辆的稳定性、安全性。

图4 车辆动力学性能指标的变化图
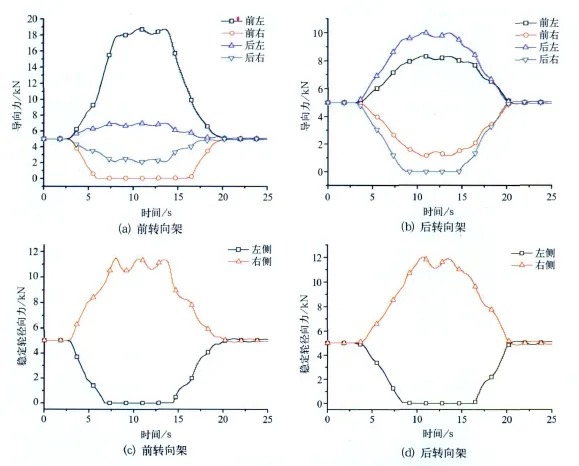
图5 导向轮和稳定轮径向力的变化曲线
由以上分析可知,对导向轮胎和稳定轮胎设置一个预压力,使之紧贴在轨道梁侧面,对保证跨坐式单轨车辆的平稳导向和安全性有重要的作用。但如果导向轮和稳定轮的预压力取得太小,在高速通过曲线或受到侧向强风作用时,有可能会造成某些导向轮或稳定轮与轨面分离,从而影响车辆的运行安全性和稳定性;如果导向轮和稳定轮的预压力取得过大,则增加了车辆的运行阻力,容易造成轮胎过快地磨耗,并对转向架的强度产生不利影响。因此为了确定导向轮和稳定轮初始压力,需要综合考虑线路的曲线半径、超高,车辆的运行速度,侧向风的作用,轮胎强度以及走行部结构强度等因素,确保车辆在各种运行条件下,导向轮和稳定轮与轨道梁之间没有间隙,即导向轮和稳定轮对轨道的压力不应该为零,在此前提下,尽量取小值,对于本文的单轨交通车辆系统,根据仿真结果将导向轮、稳定轮的预压力取10 kN时可保证导向轮稳定轮在运行时既不脱离轨道也不至于太大而增加摩擦力的消耗,还可使车体、转向架运行时的侧滚角较小,从而保证车辆的运行安全性。
5 结束语
通过受力分析和仿真计算可知,导向轮、稳定轮的预压力对单轨车的运行安全性有重要的影响,预压力太小不能起到保证车辆运行安全的作用,但预压力过大会增加运行阻力。因此,应综合考虑车辆运行的各种条件选择合理的预压力,从而既保证车辆的运行安全也不至于使车辆运行阻力增加太大,对于本文的单轨交通车辆系统,将导向轮、稳定轮的预压力取10 kN比较适宜。
[1] 张建全,黄运华,李 芾,等.独轨交通的发展及其在城市轨道交通中的应用[J].铁道机车车辆,2009,29(1):25-30.
[2] 刘绍勇.重庆跨坐式单轨转向架的研制[J].铁道车辆,2003,41(9):18-21.
[3] 王省茜.跨坐式单轨铁路的特点及其应用前景[J].中国铁道科学,2004,25(1):131-135.
[4] Kenjiro Goda,Nishigaito T,Hiraishi M.A curving simulation for a monorail car(C).Railroad Conference,Proceedings of the 2000ASM E/IEEE Joint.2000,171-177.
[5] Lee Chang Hun,Kim Chul Woo,Kawatani M,et al.Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains[J].Engineering Structures.2005,27(14):1999-2013.
[6] Lee C H,Kim C W,Kawatani M,et al.Dynamic response of a monorail steel bridge under a moving train[J].Joumal of Sound and Vibration.2006,294(3):562-579.
[7] 严隽耄,傅茂海.车辆工程(第三版)[M].北京:中国铁道出版社,2008.
[8] 任利惠,周劲松,沈 钢.跨坐式独轨车辆动力学模型及仿真[J].中国铁道科学,2004,25(5):26-31.

