基于ANSYS对罐体垂向载荷施加方法研究*

杨亮亮,傅茂海,安 琪,邵朋朋

(西南交通大学 机械工程学院,四川成都610031)

罐车是一种车体主要结构呈罐形的车辆,用来装运各种液体、液化气体及粉末状货物等,其罐体属于运动中的压力容器。设计满足压力容器相关标准、结构强度和轻量化要求的罐车罐体是保证运输安全和降低成本的前提。其中如何模拟罐体垂向载荷的施加方法对设计阶段准确评估产品的性能有着至关重要的影响。由于罐车内的货物和罐体之间存在接触问题,所以有限元模型中载荷的施加变得比较复杂。为了能够方便而准确的利用ANSYS对罐体进行有限元计算分析,一般在分析模型中采用如下几种方法对罐体垂向载荷进行模拟:

(1)直接将货物重力的影响等效为作用在罐体下半部分内壁面的垂向均布压力,忽略罐体本身几何形状的影响。

(2)等效分割法。将罐体内的货物沿纵向切分成若干部分,通过数值方法把每一部分质量换算为该处承载面的垂向载荷,即对罐体下半部分施加垂向非均布载荷。

(3)耦合自由度法。建立质量单元和接触对,通过节点自由度耦合来模拟货物和罐体内壁的接触。

(4)考虑货物和罐体接触面相互作用的影响,以接触单元为主,综合线性弹簧—阻尼单元,建立结合面的有限元模型,若装载货物为流体,需采用合理的流体单元模拟[1]。

以上几种方法中,第(1)种方法简单,但模型简化较粗糙,会造成局部应力分析的结果与实际差别很大;第(2)种方法相对第(1)种方法模型简化有所改进,但其分析结果的精度与承载面分割的份数有直接关系;第(3)种方法有较高的精度,通过简化的质量单元达到了将非线性问题的线性化,但是这(3)种方法都忽略了货物和罐体的结合面效应;第(4)种方法就是包含结合面效应的方法[2],该方法理论上比较完善,但属于非线性问题,计算复杂耗时,一些参数又需要试验测定,并且测定比较难。

针对以上方法的特点,采用了等效分割和耦合自由度法两种方法来对比验证其合理性。分析结果证明,这两种方法有较高的计算效率和计算精度,对模拟罐体垂向载荷可以提供一定参考价值。

1 罐体垂向载荷施加方法的研究

如上所述,采用等效分割与耦合自由度两种方法能够方便而比较准确的利用ANSYS软件进行计算分析,下面就这两种方法在ANSYS模型中的应用进行分析。

1.1 等效分割法

该方法是将罐体内的货物沿纵向切分成若干部分,并把每一部分质量换算为该处承载面的垂向载荷,即对罐体下半部分施加垂向非均布载荷。具体方法如图1所示的3组货物分割模型,这里假设货物顶部处于水平状态。其中图1(a)是将货物按照罐体的几何形状沿着纵向等距切分成6份的简化模型,图1(b)和图1(c)依次将货物分割成12份和24份,倘若将货物无限切分下去就成为了图1(d)中的模型,这也是实际情况下的货物装载效果图。

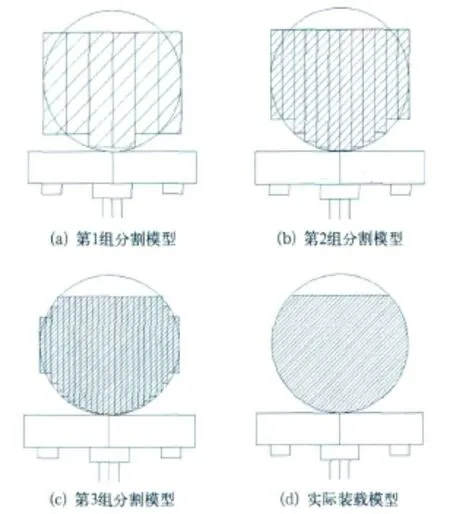
图1

由于研究的工况基本都属于静态或准静态载荷工况,而且罐体的几何形状是对称的,此情况下切分后的货物之间产生的相互影响可以忽略,这为建立的等效分割模型的合理性提供了一定的依据。通过计算得出每一份货物质量作用于相应罐体承载面的垂向压力。

式中i表示份数;j表示组数;M表示货物总质量;Aij表示第j组第i份货物断面面积;g表示重力加速度。i的值越大,罐体承载面所作用的等效垂向压力的分布就越均匀。此外,还需要考虑罐车车体自身的重力以及罐内气体压强的影响。

1.2 耦合自由度法

由于罐体和罐装货物之间存在接触问题,是一种高度非线性行为,尽管模拟出罐体和货物之间结合面效应可以使模型的计算结果更精确,但是计算成本很大。在ANSYS模型中,如果不考虑摩擦,且物体之间总是保持接触,则可以应用约束方程或自由度耦合来代替接触。如果建立约束方程[3],则必须满足:

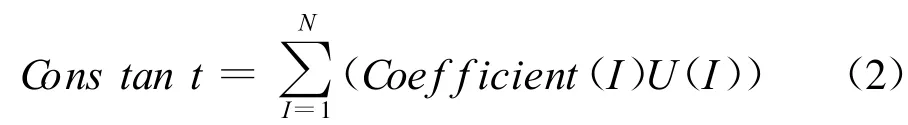
式中U(I)是自由度项,一般包括3个平动和3个转动自由度;N是方程中项的编号。约束方程迫使这些自由度之间取得线性的关系。

而耦合自由度就是建立一个耦合设置,使其被约束在一起,并具有相同的自由度。但是耦合的应用必须具备下列4个条件[4]:

(1)表面保持接触;(2)小变形分析;(3)忽略摩擦;(4)在两个界面上,节点是一一对应的。

显然,对于罐体垂向载荷的分析可以满足以上4个条件,因此利用耦合自由度方法来模拟接触面是合理可行的,并使分析简化为线性问题,大大节约计算资源和时间。

假设货物的密度是均匀分布,为了要确定货物重心位置,只需要找到货物形心位置,建立如图2所示的罐体断面模型。

图2 罐体断面计算模型

取对称轴为y轴,则形心必位于该轴上,再在距z轴为任意高度y处取平行于z轴的微面积dA,则货物断面积相对于z轴的面距为:

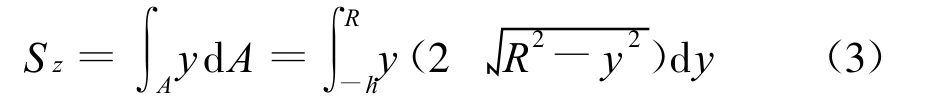
式中R为罐体半径;h为货物装载高度。设断面形心C的坐标为yC,则:

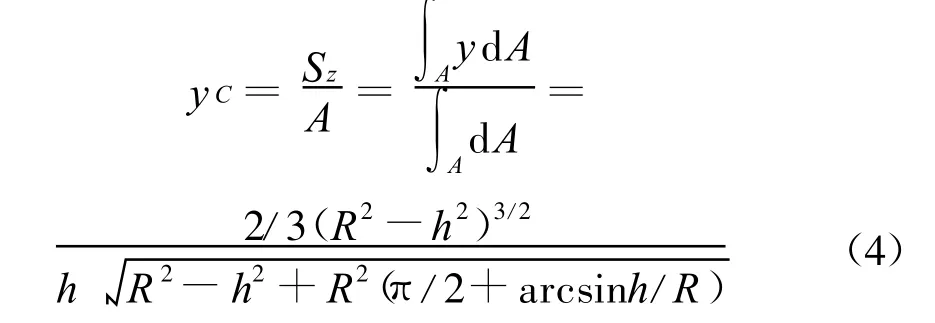
然后将罐体内的货物在其重心位置处用质量单元来代替,且赋给实际货物的相关属性,并将质量单元和罐体承载面进行耦合自由度,建立接触对来模拟货物对罐体的影响。

2 计算实例

2.1 有限元模型的建立

以某有底架罐车车体为对象,用ANSYS软件建立其有限元分析模型。

罐车车体主要由罐体和底架等组成。罐体由筒体、封头、鞍座、防波板等零部件组焊而成。筒体半径1 104 mm,厚度8 mm;封头为球形封头,厚度10 mm。底架主要由中梁、枕梁、端梁及侧梁等部分组成。罐体中部的上鞍与底架中部的下鞍用螺栓进行连接,同时罐体落于枕梁鞍座处。利用ANSYS有限元分析软件建立模型并离散[5],整个罐车车体钢结构共划分为78 200个节点,65 880个板壳单元。在上心盘处施加边界条件,边界条件采用弹性体边界元处理,其刚度参照转向架的悬挂刚度,整车共有24个边界元。车体的有限元模型如图3所示。

图3 罐车车体有限元模型

2.2 载荷工况的计算

按照有关标准和技术条件的要求,对该罐车车体钢结构进行有限元静强度分析计算时考虑以下几种载荷情况:

工况Ⅰ:垂向静载荷+自重+0.28 MPa罐内压力;

工况Ⅱ:(垂向静载荷+自重)×1.6+0.28 MPa罐内压力+150 t纵向拉伸力;

工况Ⅲ:(垂向静载荷+自重)×1.6+0.28 MPa罐内压力+150 t纵向压缩力;

工况Ⅳ:垂向静载荷+自重+0.28 MPa罐内压力(顶车工况)。

罐车车体钢结构为板材拼组的焊接结构。板材或者型材材料采用Q345高强度低合金结构钢。冲击座的材质为C级铸钢。根据该罐车技术条件规定,罐车车体应在各个加载的载荷综合作用下,当量应力应不大于材料的屈服极限(345 MPa)。当量应力按下列公式计算:

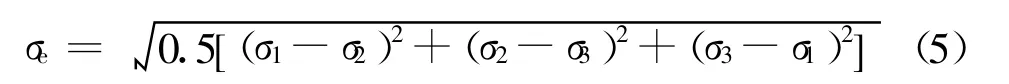
式中 σe为当量应力,MPa;σi为主应力(i=1,2,3),MPa。

2.3 计算结果对比与分析

采用不同的垂向载荷处理方法,4种载荷工况中罐体的最大应力分析结果见表1,在表1中,以耦合自由度法计算结果为基准值,计算其他方法计算结果的相对误差。

从表1中可以看出,最大应力主要发生在罐体与防波板连接处和罐体与鞍座连接处,与实际是相吻合的。各组合工况下的最大应力均小于其许用应力,满足标准要求。对于工况Ⅱ和Ⅲ中出现最大应力发生位置不一致的情况,是由于将货物分割成图2(a)和图2(b)时,靠近罐体和防波板连接处的那部分货物质量偏大,于是该处等效的承载面受力也偏大,从而导致了部分组合工况下局部应力的差异。

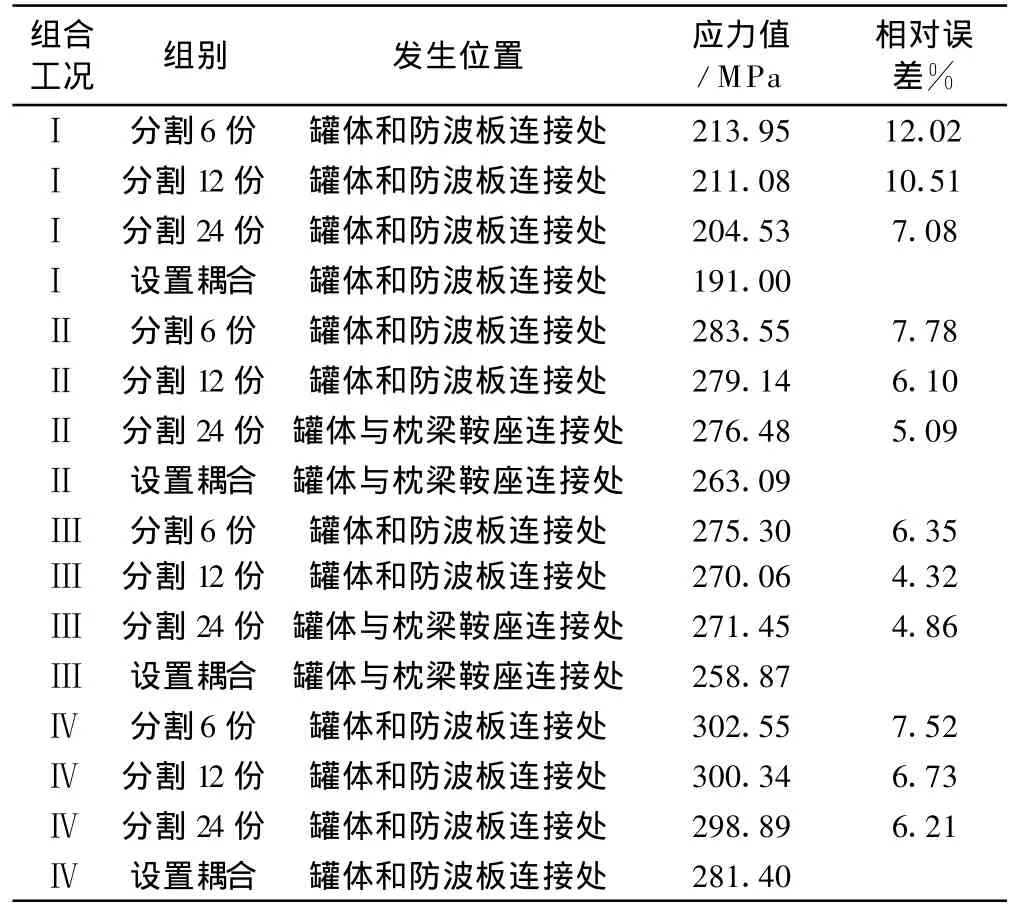
表1 最大等效von_Mises应力及其位置

图4 垂向静载荷工况下等效von_Mises应力云图

为了更好的比较分析等效分割法与耦合自由度法两种方法的准确性,下文分析了在垂向静载荷工况下的计算结果,从而能更直观的看到不同罐体垂向载荷施加方法对罐体结构的强度和刚度影响。

图4为垂向静载荷工况下的等效von_Mises应力云图,其中图4(a)、图 4(b)、图4(c)和图4(d)分别代表分割6,12,24份和耦合设置4组情况,从图中可以看出其最大应力区域的应力分布基本相同,并且整体应力分布呈现逐渐逼近的趋势。

图5为垂向静载荷工况下部分区域最大节点应力统计曲线图。其中第1组曲线为利用耦合自由度法得到的垂向静载荷工况计算结果,提取了罐体结构中10个关键区域处的节点最大应力值,其中节点1～4在罐体和防波板连接处;5～8在罐体与枕梁鞍座连接处;9和10在罐体球形封头过渡处。并利用等效分割法将这10个节点在分割6,12,24份情况下的应力值分别列出,即图5中第2,3和4组所示。

从图5可以看出,在罐体和防波板连接处以及球形封头过渡处,用等效分割法计算的应力结果比耦合自由度法的计算结果大;而在罐体与枕梁鞍座连接处,用等效分割法计算的应力结果比耦合自由度法的计算结果小,但是4组结果的相对误差不大。同时可以看出,分割的份数越多,计算结果就越接近耦合方法的计算结果,说明耦合自由度方法较等效分割法更准确。

图5 部分节点应力在各组情况下的应力值

图6为垂向静载荷工况下的罐体位移变形图,其中图6(a)、图6(b)、图6(c)和图6(d)分别代表分割6,12,24份和耦合设置4组情况,从罐体中心断面处观察可以看出其位移变形基本一致,也呈现逼近趋势。

3 结论

(1)用等效分割法模拟罐车货物对罐体的影响,基本可以准确地得到罐体的整体位移和应力分布。随着分割份数的增加,局部位移和应力的分布会更精确。

(2)用耦合自由度法来模拟货物和罐体的接触面,使接触非线性问题变成线性问题,不仅大大节约计算资源,并且能准确的得到整体和局部的计算结果,更与实际相吻合,且载荷施加更加方便。

图6 垂向静载荷工况下的罐体位移变形图

(3)通过对罐车罐体垂向载荷施加方法的探讨和计算实例的对比验证,两种方法分析结果在罐体强度和刚度上都基本一致,均能满足一般工程应用的要求,对铁路罐车车体的结构分析有一定的参考价值。

(4)对于如黏油罐车等而言,货物与罐体之间的摩擦力可能相对较大,如果货物和罐体的结合面效应对研究对象的影响不能忽略,就需要利用有限元方法建立接触单元进行非线性分析,并考虑试验条件下的摩擦系数、黏性系数等货物材料特性。

[1] 赵 勇,张若京,孙利民.G70B列车油罐液固耦合模态分析[J].计算机辅助工程,2007,16(3):119-122.

[2] 秦绪柏,陈 南,等.耦合结点子模型法在螺栓联接结构分析中的应用[J].精密制造与自动化,2003,153(1):32-33.

[3] 黄明高,姚曙光.耦合与接触非线性在铁道罐车车体结构分析中的应用[J].铁道机车车辆,2007,27(6):23-26.

[4] 傅茂海,安 琪,杨亮亮.出口孟加拉国罐车车体强度报告[R].重庆长征重工有限责任公司,2010.

[5] 严隽耄,傅茂海.车辆工程(第 3版)[M].北京:中国铁道出版社,2008.

[6] 王勖成,有限单元法[M].北京:清华大学出版社,2003.