基于FLUENT的固体火箭发动机点火瞬态内流场仿真影响因素分析①

杨 乐，余贞勇，何景轩

(中国航天科技集团公司第四研究院第四十一研究所，固体火箭发动机燃烧、热结构与内流场国防科技重点实验室，西安 710025)

0 引言

固体火箭发动机点火瞬态过程是一个机理复杂的非定常过程，包括药柱加热、局部点燃、火焰沿药柱表面传播和燃烧室增压等过程。点火瞬态过程发生异常，如出现过大点火延迟、过高压强峰值等，会导致发动机工作失效，甚至可能造成严重后果。所有这些现象与发动机几何形状、推进剂物性参数、点火器及其位置等有密切关联。定量预示发动机点火瞬态过程，揭示点火瞬态的内流场特性，有利于对发动机点火效果的影响因素进行分析，便于调整参数和改进设计，从而提高发动机质量比[1]和安全性。

国内外许多学者[2－4]都对发动机的内流场进行了大量的数值分析，但对于在FLUENT中影响仿真结果的具体因素，则较少进行深入研究。因此，本文选取了影响点火瞬态内流场仿真的主要因素进行分析比较。首先，由于实际点火器结构较为复杂，需要对其进行简化处理，通常采用等效面积法将侧向喷孔简化成环形缝，环形缝位置不同将会对仿真结果有不同的影响;其次，在FLUENT软件设置中，对于相关参数的输入可采用常值简化处理，也可利用UDF接口给出更接近实际情形的取值，不同的处理方式也会影响仿真结果;最后，对于点燃方式的选取，通常认为推进表面温度达到点火温度即为推进剂点燃，这使得仿真结果所得到的火焰传播速度往往大于试验值，从而导致最终模拟结果的精确程度出现较大偏差。鉴于此，采用更为合理的点燃方式则是解决此类问题的有效途径。

本文采用三维物理模型，模拟大长径比固体火箭发动机不同情形的点火升压过程。同时，该类固体火箭发动机的点火瞬态过程压强、推力等变化剧烈，火焰传播过程较长，对其仿真能更好反映出上述点燃方式对模拟结果的影响。

1 计算模型

1.1 发动机内流场结构

计算模型如图1所示，考虑翼槽的对称性，取1/8进行模拟仿真。

图1 流场结构Fig.1 Flow field structrue

1.2 数学模型

为便于计算，对模型作如下假设:

(1)由于点火过程非常短暂，在计算中不考虑发动机内流场与结构之间的耦合关系;

(2)燃烧所生成的混合气体为理想气体;

(3)点火瞬态不计侵蚀燃烧，推进剂燃速只与当地压强有关;

(4)点火器燃气与推进剂燃气具有相同性质，忽略各组分间化学反应，忽略比定压热容随温度的变化，取为常数;

(5)采用动态温度点火方式，即相对于通常取燃面附近流体单元温度达到恒定点火温度作为点燃判据而引入的定义。其以固体推进剂薄层内部表面达到点火温度为依据，在考虑燃面与流场的对流换热特性及推进剂燃烧时自身的化学反应过程中吸、放热等各个因素共同作用的基础上，引入随点燃处推进剂燃速变化的转换因子将此恒定的点火温度转化为在数值模拟中容易获取的燃面附近流体单元的动态点火温度，进而将其作为推进剂的点燃判据。

1.3 控制方程

流场燃气采用非定常可压缩N-S方程，以连续、动量和能量方程为基础，考虑气体粘性和热扩散率随温度的变化关系;湍流模型采用RNGk-ε两方程模型，该模型可更好地处理高应变率及流线弯曲程度较大的流动;近壁区由于Re数较低，湍流发展并不充分，湍流的脉动影响不如分子粘性大，所以采用标准壁面函数法处理。

为考察脉动影响，目前对湍流广泛采用的方法是时间平均法。时均化的N-S方程通用表达式[5]为

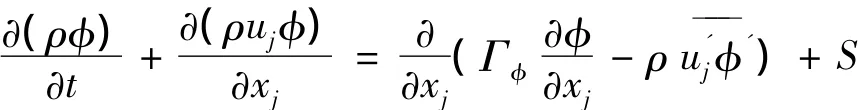
式中 φ为通用变量(φ=1，u，v，T分别对应连续、动量和能量方程);Γφ为与φ相对应的广义扩散系数;湍流脉动能附加项是与φ相对应的湍流扩散系数);S为广义源项，包含有两项间的相互作用。

1.4 初始及边界条件

初始条件:该发动机为地面静止试验发动机，且燃烧室初始冲入压强为0.1 MPa，环境压强为0.094 8 MPa，因此整个流场区域的初始状态取为:T=300 K，p=0.194 8 MPa，3个方向的初始速度为零。

边界条件:

(1)点火器出口采用质量流率边界条件;

(2)发动机头部为绝热边界;

(3)药柱表面为热耦合边界，即燃面点燃前按加热表面处理;点燃之后按侧壁加质边界进行处理;

(4)喷管出口在堵盖打开后设为压力出口边界条件;堵盖在打开前其为固体壁面边界条件，打开后为内部边界条件。

1.5 计算方法

文中利用UDF接口编程进行二次开发[6－7]，采用侧壁加质的方法设定固体推进剂燃面边界，点火判据采用动态温度点火方式。由于发动机燃烧室在点火瞬态期间压强、温度迅速上升，会造成燃气热导率远大于固体推进剂的热导率[8]。本文采用的转换因子的变化规律为与点燃处推进剂燃速呈线性关系，随燃速增加而减小，变化范围约为0.96～0.85。根据点火器的压强-时间曲线，在保证总质量流量的前提下对点火器燃气流量进行了假定。

计算过程以堵盖打开为分界线，将整个工作过程分为两部分，堵盖打开前设为壁面边界，打开后设为内部边界条件，同时将之前的计算结果作为初始条件进行计算，直到发动机点火瞬态过程完成。取1/8整翼进行计算，由于发动机翼槽呈周向均匀分布，此简化方式可较准确地接近实际情形。利用有限体积法建立离散方程，压强和密度耦合方式在堵盖打开前选用PISO算法，堵盖打开后选用SIMPLE算法，守恒方程采用一阶迎风格式，时间步长设置为1×10－5s。

2 计算结果及分析

在以上物理模型的基础上，选取了4种组合方式进行分析，如表1所示。所模拟的燃烧室头部压强和试验所测压强的结果如图2所示。其中由于点火器侧向喷孔呈周向非均匀分布，三维建模较为复杂，且划分网格时不容易生成高质量的三维网格，则采用等效面积法对其进行2种方式的简化。

2.1 不同点火器简化方式的影响

对比表1中方式1和方式2，可看到前者升压速率明显高于后者，表明其火焰传播速度较快，在0.12 s时刻已经接近稳态工作压强，与试验值不一致。这是因为初始阶段采用方式1简化处理的点火器会使引燃主药柱面积较大，从而在随后的升压过程中，其累积效应更加明显，使所模拟的升压过程中不同时刻的压强值均高于方式2。图3为2种方式下4、50 ms时刻的燃烧室头部温度云图。由图3(a)、(b)可见，2种方式下引燃的主药柱初始点火位置明显不同，方式1的初始点燃位置相对方式2要远离头部，这是因为虽然燃气同样在头部发生聚集，但在进口燃气的冲击点，温度升高会更快速，从而在正对点火器出口处的单元会先被点燃。另外，图3(c)、(d)也显示出方式1火焰传播速度要高于方式2。

表1 参数组合方式Table 1 Method of parameter combination

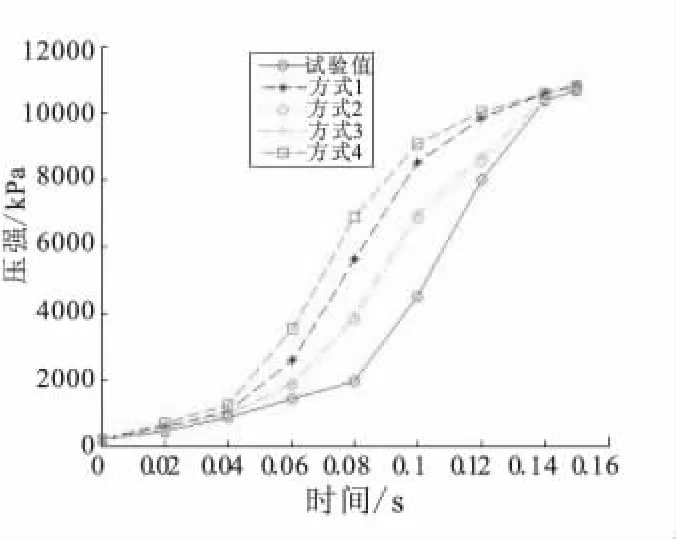
图2 计算值与试验值对比Fig.2 Comparison between calculation and experiment value

图3 不同时刻温度云图对比Fig.3 Comparison of temperature contour at different times

2.2 不同点火器出口参数选取方式的影响

对比表1中方式2和方式3，二者的升压速率相差不大。整个模拟过程以0.02 s时刻为分界点，之前二者压强相差较大，之后差距则有所降低。这是因为初始阶段引起燃烧室压强升高的因素中，点火器燃气的加入占据主导作用。方式3以点火器出口燃气的平均值加入，显然在达到点火器峰值时间之前所加入的燃气总质量相对较多，导致模拟的升压速率会大于前者，随着时间的推进，方式2在点火器峰值期间引燃主药柱面积会比后者显著增加，升压速率大于后者，从而在点火器峰值附近时刻二者燃烧室压强相差会很小。此后，燃烧室压强的增加主要由主药柱的加质来决定，点火器的贡献相对则很小，且二者的其余边界条件相同，升压规律基本相同。图4为3、45 ms时刻的温度云图。由图4(a)、(b)可见，方式3的初始引燃面积明显大于方式2。另外，图4(c)、(d)显示出二者的主药柱点燃面积已经相差很小。

2.3 不同点燃方式的影响

对比表1中方式2和方式4，方式4的升压速率相对较高，其达到稳态工作压强的时间也必然早于方式2。其原因在于点火瞬态期间，气体温度的升高速率会明显大于固体推进剂表面温度的升高速率，方式4以燃面附近气体单元温度达到点火温度为依据，会使所模拟的火焰传播速度高于实际值。而方式2考虑了对流传热及各种影响因素对火焰传播的影响，选择固体推进剂薄层内单元温度达到点火温度作为点燃判据，同时利用转换因子将此恒定的点火温度转化为燃面附近流体单元的动态点火温度，以满足与实际点火过程的流场状态更加吻合，因而模拟的点火瞬态过程的压强值与试验值基本一致。图5为40 ms时刻的温度云图。由图5可见，方式2的主药柱点燃面积要小于方式方式4，反映出方式2相对方式4有效地降低了火焰传播速度，使得仿真结果更为准确。

图4 不同时刻温度云图对比Fig.4 Com parison of tem perature contour at different times

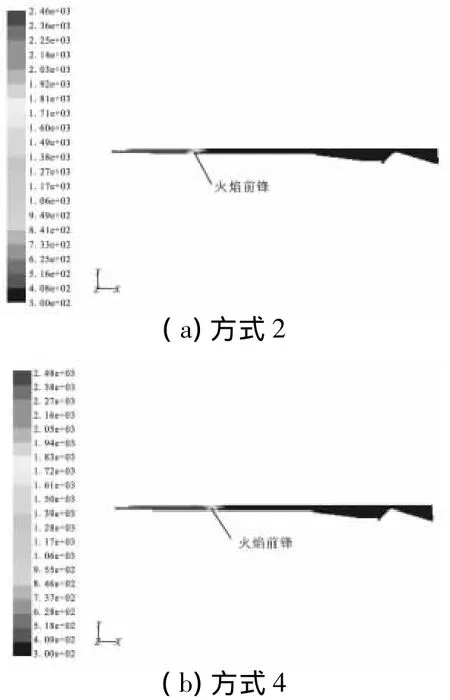
图5 40 m s时刻温度云图对比Fig.5 Com parison of tem perature contour at 40 m s

3 结论

(1)点火器侧向喷孔沿轴向简化为多条环形缝结构时，主药柱初始点火位置更靠近头部，仿真值与试验值基本吻合。

(2)流量入口边界条件中各数值采用平均值和采用实测值在点火器压强达到峰值附近时刻之前升压规律不同，其后则基本一致。

(3)燃面加质边界条件中点火温度判据采用恒定值会导致仿真的火焰传播速度明显加快，而考虑了传热影响的动态点火温度判据所模拟出的结果则更好地反映了实际情形。

[1] 方丁酉，等.固体火箭发动机内弹道学[M].长沙:国防科技大学出版社，1997.

[2] 刘君，郭正，等.非结构网络技术应用于固体火箭发动机数值模拟[J].固体火箭技术，2001，24(4):9-11.

[3] Cang S T，Han S，Joh C.Radiation effect ignition on I-D transient anlysis of SRM[R].AIAA 96-3055.

[4] 陈军涛，蹇泽群，陈林泉.固体火箭发动机点火瞬态内流场轴对称数值分析[J].固体火箭技术，2004，27(3):183-176.

[5] 王福军.计算流体动力学分析[M].北京:清华大学出版社，2004.

[6] 周志清，高双武.含装药缺陷固体火箭发动机点火瞬态内流场的数值研究[D].第二炮兵工程学院，2006.

[7] 孙淑霞，肖阳春，等.C/C++程序设计教程[M].北京:电子工业出版社，2009.

[8] 匹茨D R，西逊姆L E.传热学的理论和习题[M].上海:机械工业出版社，1983.