不同主流速度下障碍涡脱落冷流实验研究①
甘晓松,何国强,杨尚荣,岳 赟
(西北工业大学燃烧、热结构与内流场重点实验室,西安 710072)
0 引言
现代固体发动机尽管采用了含铝复合固体推进剂,但大长径比固体火箭发动机仍然受到燃烧不稳定的困扰。为解决大型分段式装药固体发动机的燃烧不稳定问题,美国和欧洲都投入了大量的人力和物力。美国开展的多学科大学研究倡议(MURI:Multi-Disciplinary University Research Initiative)试图从基础化学、燃烧和流体动力学的角度深入研究燃烧不稳定问题[1];以法国为主的欧洲启动两大研究计划研究燃烧不稳定问题:分段固体发动机气体动力学(ASSM:Aerodynamics of Segmented Solid Motors)和压强振荡计划(POP:Pressure Oscillation Programs)[2]。ASSM 的主要科学目标是对涡脱落进行深入理解和建模,促进数值模拟技术的发展。POP计划是利用P230的缩比模型发动机开展实验研究,获得实验和数值数据库,加强对分段发动机中涡脱落导致压强振荡现象的理解,寻求燃烧不稳定的抑制方法。国外研究初步表明,声涡耦合产生的共振是大长径比固体发动机燃烧室压强振荡的源头,当推进剂的压强耦合响应等增益作用强于两相流阻尼等抑制作用时,就会出现较为强烈的压强振荡。为深入了解涡产生的条件、涡与发动机结构的固有声模式耦合的条件等,需要用冷流实验的方法研究燃烧室的气体动力学过程。ASSM-POP项目中一部分研究采用冷流实验装置,如 ONERA的 VECLA[3]和VALDO[4-5]及冯·卡门流体动力学研究中心(VKI)的冷流实验器[6-7]。
大长径比固体火箭发动机可能存在3种类型的涡脱落[8]:障碍涡脱落(OVS)、转角涡脱落(AVS)和表面涡脱落(SVS)。针对障碍涡脱落,Anthoine J等[9]采用P230的1/15缩比实验器,测试了障碍物高度和障碍物间距之比h/L与压强波动的关系;Yildiz D[10]研究了障碍物在试验器中的位置对压强振荡的影响;压强振荡随障碍物刚度的变化规律在文献[11]中做了考虑;为了观察旋涡的配对现象,PIV(particle image velocimetry)技术[12]被用来显示试验器内部的流动细节。
本文使用高速摄影平台[13]和压强测试系统来研究不同主流速度下障碍涡脱落的产生规律及脱落涡与试验器声腔耦合对压强振荡的影响。高速摄影技术可捕获涡脱落的整个运动过程,这无疑可加深对声涡耦合机理的理解。
1 实验系统
冷流试验系统主要由空气供给系统、冷流实验器、高速摄影系统、压力测试系统及示踪粒子加入系统等组成,如图1所示。
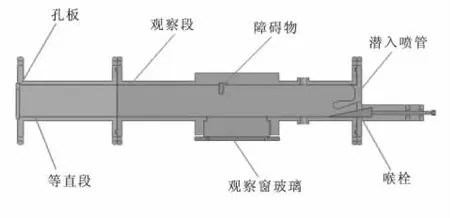
图1 冷流实验器结构示意图Fig.1 Schematic diagram of cold flow experimental equipment
1.1 冷流试验器
为了便于高速相机对实验器内流场进行拍摄,实验器采用二维结构,在障碍物附近区域开有观察窗和光源窗。整个冷流实验器分为多段,主要包括以下几部分:
(1)进气段:主要负责与空气供给系统相连,并确保气流稳定和均匀,进气段开有传感器孔,用于测量孔板前的气流压强。
(2)多孔板:主要是隔断气流上、下游之间的声波传播,以便能够获得确定长度的冷流实验器声腔。
(3)等直段:来流经过孔板后,需要经过一段较长的距离使产生的旋涡耗散。在该段开有传感器孔,测量孔板后的压强,即工作段的静态压强。
(4)观察段:该段安装有障碍隔板,在其附近开有观察窗来实现对旋涡产生、脱落和传播的观察,并对该过程进行拍摄。
(5)喷管段:设计了一个潜入式喷管。
1.2 高速摄影系统
PIV和PLIF技术在流场显示中广泛应用,但这2种方法使用的都是频率约30 Hz的脉冲激光器,只能得到流场的瞬态情况,对于频率较高的情况就有不足。故本文试验采用高速摄影系统来记录障碍涡脱落的整个动态过程,通过对拍摄图像的后处理,可得到半定量的测量结果。
本文采用的高速摄影系统主要包括激光器、片光转换装置和高速数字相机,原理如图2所示,图2中黑点为示踪粒子。示踪粒子加入装置见图3,示踪粒子选用粒径为1~10μm的Al2O3粉末。

图2 高速摄影系统示意图Fig.2 Schematic diagram of high speed camera system

图3 示踪粒子加入装置Fig.3 Supp ly equipment of trace particle
固体激光器提供持续的光源,激光方向可通过光导臂转换。片光源转换装置可将点激光转换为片光源照射在流场区域。同时在垂直于片光源的方向放置高速数字相机进行拍摄,利用流场中铝粒子的散射作用,就可获得二维流场区域内的旋涡运动情况。
1.3 压强测试系统
障碍涡脱落引起声涡耦合后,最直接的表现就是压强振荡,因此实验中压强测试系统是最为关键的部分。本实验中要测试的压强信号主要包括2种:静态压强和动态压强。静态压强是指实验器稳定工作时内部的平衡压强;动态压强是指在稳定工作时,基于平衡压强上下波动的波动值,即所谓的声压。对于静态压强的测量,可使用普通的压强传感器。但对于动态压强,由于冷流实验中压强振荡的振幅相对较小,故必须使用灵敏度较高的压电式传感器。测量时,压电式传感器首先获得振荡的电荷信号,然后通过电荷放大器转换为电压信号,再通过数据采集系统转化为压强信号。本文静态压强测试使用常规的DaCY420传感器,动态压强测试采用国产CY-YD-211压电式传感器,灵敏度为6 960 pC/105Pa(静标)。
2 实验结果与分析
2.1 压强测量结果分析
通过冷流试验器喉栓的调节,通道主流速度可在Ma=0.07~0.18之间连续变化,每次调节增量Ma=0.01。试验后,利用快速傅里叶变换(FFT)对测得的压强信号进行分析,获得压强振荡的振幅和频率如图4所示。

图4 动态压强FFT分析Fig.4 FFT analysis of dynam ic pressure
由图4可看出,当主流速度为Ma=0.10和Ma=0.11时,在频率为616 Hz处存在较为明显的压强振荡,其振幅分别为10.4 Pa和6.65 Pa。对比试验器声场分析结果可知,616 Hz与实验器的三阶轴向固有频率基本相近。在其他工况下,虽然在前三阶固有频率附近均存在一定程度的振荡,但幅值都较小。
图5为高速摄像图片,每幅图片中均保留了拍摄时间,其中Δt=343~345μs。由图5可见,当主流速度为Ma=0.07时,旋涡不很明显,且无规律,脱落的旋涡很快就向上卷起,耗散的非常快。对应的压强测试结果显示该流速下没有明显的压强波动。利用声涡耦合的理论进行分析,认为涡的脱落不稳定,没有规律,就无法作为源头激发具有“属性”性质的试验器声腔的固有模态,也就不存在与之进一步形成有效耦合的可能性。当主流速度增加到Ma=0.11时,旋涡的脱落较为规律,在t时刻,有 A、B 2个旋涡,经过4Δt时间之后,旋涡B运动到原来旋涡A的位置,新产生1个旋涡C处于原来旋涡B的位置,经过8Δt时间之后,旋涡C、D代替了之前的旋涡B、C。据此估算此时旋涡脱落的频率约为724 Hz。

图5 高速摄影图片Fig.5 Experimental images of the high speed camera
其与试验器声场的三阶固有频率(616 Hz)比较接近。压强测试也表明此时试验器发生了频率为616 Hz、振幅为6.65 Pa的压强振荡,故可推断涡与试验器内部声场发生了耦合作用,从而产生了自激振荡。
当主流速度提高到Ma=0.13时,障碍物后的旋涡脱落带很明显,在t时刻产生旋涡A,经过3Δt时间之后,旋涡B运动到原来旋涡A的位置,估算出旋涡脱落的频率约为966 Hz。该频率与实验室声腔的五阶频率1 019 Hz相近。结合压强测量结果可知:Ma=0.13时的共振强度与Ma=0.11时相比微乎其微,似乎违背了声涡耦合理论中的“锁频”现象。分析原因认为,一方面激发声场的高阶模态且发生共振相比于低阶模态需要更多的能量[14],且声涡耦合过程中传递的能量不足以完成高阶模态的激发;另一方面,作为示踪粒子加入的Al2O3粉末(粒径为1~10μm)对高频振荡有很强的阻尼作用[15]。这两方面原因可能导致试验器没有出现高阶的压强振荡。
随着主流速度进一步提高到Ma=0.15时,在t时刻有一个旋涡A;经约2Δt~3Δt时间之后,旋涡B代替了原来的旋涡A,估算旋涡脱落频率在1 208 Hz左右,其与试验器声腔的六阶固有频率(1 190 Hz)接近,但同样没有产生压强波动,其原因分析同上。
同时,随着“可能”被激发的模态的升高,粒子的阻尼作用与激发振荡所需的能量都将进一步增强和增多,据此推断当主流速度达到Ma=0.18时,更不会产生振荡。当主流速度为Ma=0.18时,旋涡脱落的频率又有升高,在t时刻有一个旋涡A;经过2Δt时间之后,旋涡B代替了原来的旋涡A;经过4Δt之后,旋涡C代替了原来的旋涡B,估算得到旋涡脱落的频率约为1 449 Hz,接近于试验器的七阶固有频率(1 390 Hz),但没有压强波动发生,验证了推断的正确性。
3 结论
(1)本文建立的冷流试验方案合理可行,结合高速摄影对障碍涡脱落进行了初步研究,获得了几乎连续的涡的运动情况。
(2)试验结果初步表明,随着主流速度的提高,障碍物处旋涡脱落的频率相应增加,障碍涡脱落的频率与主流速度基本上是递增关系。
(3)初步研究表明,在某一主流速度下,当旋涡脱落的频率与实验器声场的某一低阶固有频率接近时,会发生压强振荡,且两者频率越接近,则振幅越大。
[1] Blomshield FS.Summary ofmulti-disciplinary university research initiative in solid propellant combustion instability[R].AIAA 2000-3172.
[2] Fabignon Y,Dupays J,Avalon G.,et al.Instabilities and pressure oscillations in solid rocketmotors[J].Aerospace Science and Technology,2003(7):19-200.
[3] Avalon G.Flow instabilities and acoustic resonance of channels with wall injection[R].AIAA 98-3218.
[4] Avalon G,Josset T.Cold gas experimental applied to the understanding of aeroacoustic phenomena inside solid propellant boosters[R].AIAA 2006-5111.
[5] Cerqueria S,Avalon G,Feyel F.An experimental investigation of fluid-structure interaction inside propellant rocketmotors[R].AIAA 2009-5427.
[6] Anthoine J,Olivari D.Cold flow simulation of vortex induced oscillations in a model of solid propellant boosters[R].AIAA 99-1826.
[7] Anthoine J,Lema M R.Comparison of different passive control solutions for reducing SRM pressure oscillations using cold flow experiments[R].AIAA 2008-4602.
[8] Guéry JF,Ballereau S,Franck G.Thrustoscillations in solid rocketmotors[R].AIAA 2008-4979.
[9] Anthoine J,Planquart P,OlivariD.Cold flow investigation of the flow acoustic coupling in solid propellant boosters[R].AIAA 98-0475.
[10] Yildiz D.Influence of radial injection flow on the aeroacoustic coupling in solid propellant boosters[R].AIAA 2001-2101.
[11] Anthoine J.Experimental study of passive control and inhibitor flexibility on pressure oscillations in large SRM[R].AIAA 2003-4671.
[12] Schram C.Sound produced by vortex pairing:prediction based on particle image velocimetry[R].AIAA 2002-2526.
[13] 陈晓龙,何国强,刘佩进.二维缩比发动机实验器中旋涡运动的实验研究[J].实验流体力学,2011,25(1),37-41.
[14] Fischbach SR,Majdalani J,Flandro G A.Acoustic instability of the slab rocketmotor[J].Journal of Propulsion and Power,2007,23(1):146-157.
[15] Blomshield FS.Lessons learned in solid rocket combustion instability[R].AIAA 2007-5803.

