无人机机载导弹落角和时间控制导引律研究①
胡凯明,文立华
(西北工业大学航天学院,西安 710072)
0 引言
在未来信息化局部战争中,作为网络中心战重要节点和打击平台的各类无人机,可居高临下快速发现、跟踪、打击各类动静态目标,无人机机载导弹也应运而生。由于无人机本身质量和尺寸的限制,无人机机载导弹一般尺寸和质量也较小,一般射程在10 km以内,作为对地对海武器可攻击地面或海上固定或低速运动目标,作为空-空弹可攻击无人机、直升机。无人机导弹攻击地面海上固定或低速运动目标时,在保证高精度的同时,不但希望命中角接近垂直,以达到最大的毁伤效果,而且希望尽可能地缩短飞行轨迹时间,以增加突防能力。对于一些有较强防空能力的目标,需多枚导弹同时攻击目标,才能使目标的防空能力不足以拦截所有来袭导弹。具有终端角度约束导引律的研究已有30多年历史,而近几年来,各国学者又加入了对命中飞行时间的控制。
文献[1]从最优控制的角度,研究了反舰导弹的命中时间控制问题。文献[2]用剩余时间多项式的形式,推导了导弹的状态方程,得到了一种控制命中角的最优导引律,并给出了较为实用且可靠的剩余时间估计方法。文献[3]对于反舰导弹结合了命中时间和落角的控制,给出了较为简单实用的既控制时间又控制角度的导引方法。
本文主要研究将文献[3]的导引律结合文献[2]的剩余时间估计方法,用于无人机机载小型空-地导弹制导,使命中时间更为精确,随后进行了数值仿真,并将文献[4]给出的电视制导无人机导引律舍去框架角约束和本文导引律进行了比较分析。
1 无人机导弹运动学模型
以目标和导弹质心为基准,将导弹与目标相对运动分解为俯冲平面和转弯平面内的运动。俯冲平面定义为导弹质心和目标及地心所确定的平面,转弯平面定义为过目标和导弹质心并垂直于俯冲平面的平面。
图1中,θ、θf为导弹速度倾角及其预定末端速度倾角;η=θ-qy,ηf=θf-qy为导弹速度矢量与视线间的夹角及其预定末端夹角;r为导弹与目标之间距离;qy为导弹与目标的高低视线角;vm为导弹速度,由于目标相对于导弹速度很小,可视为固定;ac为加速度指令,并假定导引头对目标的跟踪是理想的,也就是没有时间延迟。

图1 无人机导弹末制导俯冲平面几何关系Fig.1 UAVsmounted m issile term inal-guidance dive geometry
定义此时θ为负,则η在图1所示情况下为正,反之为负。由图1及相对运动学关系可得到:

对于转弯平面内的运动学模型与俯冲平面内的类似,定义此时弹道偏角 ψv为负,则 η=90°-qz+ψv。由图2及相对运动学关系可得:
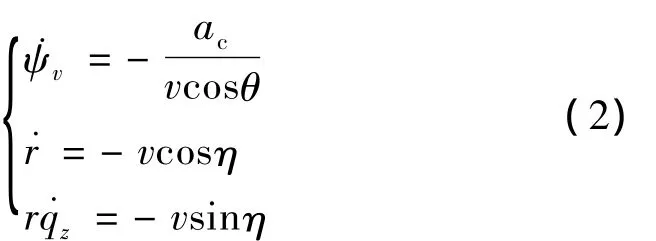
为简单起见,又能说明问题,本文采用空间三维的质点动力学弹道方程,这样就避免了姿态角为90°时而用四元素法。

图2 无人机导弹末制导转弯平面几何关系Fig.2 UAVsmounted m issile term inal-guidance turn geometry
2 俯冲平面内修正比例导引律
2.1 控制命中角导引律
命中角是指导弹速度方向和目标速度方向的夹角,由于本文假设目标为地面固定目标,故命中角在这里就是指导弹命中时的弹道倾角θ。本文采用文献[3]根据带有末端约束的最优控制理论得到的控制命中角的导引律:

式中tg0为剩余时间,预定末端落角θf=-90°。
2.2 控制攻击时间导引律
预估命中时间是指当前时间和抵达目标剩余时间之和[2]。

为实现控制命中时间,需在常规的比例导引律中引入控制命中时间修正量:

当控制修正量为正时,说明预估命中时间大于期望命中时间,此时应使导弹按照比例导引律飞向目标,也就是这种情况下,时间控制项等于零;当控制修正量为负时,说明预估命中时间小于期望命中时间,则应在导弹的飞控指令中加入和当前指令相反的量,也就是向当前弹道曲率相反的方向飞行,来增加飞行时间,从而控制导弹飞行时间[3]。于是,得到控制攻击时间导引律:

这里需说明的是选取期望命中时间时,要大于最小命中时间,本文近似认为比例导引律的命中时间为最小命中时间。
2.3 剩余时间估计
精确的剩余时间估计十分重要,本文采用了2种时间估计方法,在纵向有角度约束的情况下引用文献[2]的方法,在横侧向仅有时间约束的情况下引用文献[3]的方法。如图1定义,利用¯x和¯y及η和ηf推导剩余时间估计公式。
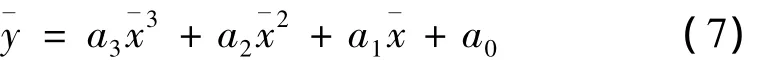
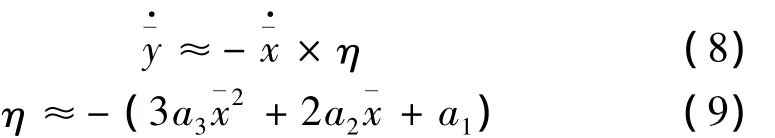
由以上几式可解得:

剩余时间可用弹目相对距离除以速度在弹目视线角上的投影在相对距离上的平均速度来近似表示[2]:
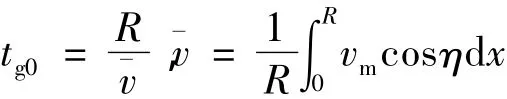
最终得到剩余时间略去高阶项的表达式:
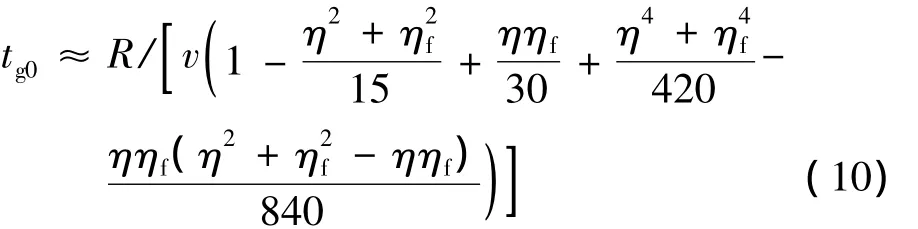
横侧向的剩余时间估计因为不考虑命中角约束,则采用弹目相对距离除以导弹速度在弹目视线角上的投影来估计:

2.4 同时考虑命中角和攻击时间的导引律
结合命中角和攻击时间两方面因素,得到带有命中角约束和时间控制俯冲平面内的修正比例导引律:

3 转弯平面内修正比例导引律
由于转弯平面内仅考虑攻击时间控制,则取消俯冲平面内的命中角控制项,即可得到带有时间控制转弯平面内的修正比例导引律:
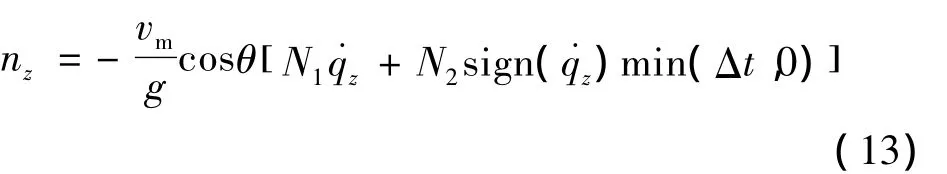
4 导引律数值仿真
通过将本文导引律用于无人机机载小型空-地导弹的导引系统来证明其优越性能,以下就2种情况进行数值仿真。
(1)情况一
对于仅控制命中角的修正比例导引律,如将文献[4]舍去框架角约束的导引律(简称文献[4]导引律)
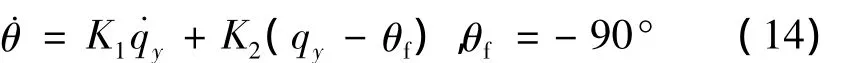
需要较大的飞行时间,降低了导弹的突防能力,而运用本文导引律,可使飞行时间tf略大于比例导引法的飞行时间,从而在保证命中角约束要求的同时,相比式(14)导引律,能较大地缩短飞行时间,增强了导弹的突防能力。
无人机从坐标(0,1 000,0)以速度vm=100m/s向正X方向飞行,目标位置在(2 600,0,1 000),单位m。比例导引律时间为t=11.15 s,则根据上面的原则,取导弹飞行时间为tf=12.5 s,导弹的初始条件为
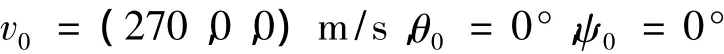
本文的导引律的各项比例系数取:

不同导引律仿真对比结果见表1。不同导引律仿真弹道对比见图3,2种导引律过载对比见图4,改进前后剩余时间对比见图5。
从仿真结果可看到,由于命中角约束项型式的不同,使得本文导引律飞行时间大大低于文献[4]中的命中角约束导引律的飞行时间,而比比例导引律的飞行时间稍大,从而增大了导弹突防概率,而且命中角也略有增大。加入了考虑命中角约束的剩余时间估计方法的时间控制项,使得剩余时间估计和理想剩余时间线几乎重合。因此,飞行时间控制得也较准确。
但从图4可看到,本文导引律在飞行末端指令过载变化增大,这给控制系统提出了较高要求,在实际应用中,可通过调节无人机小型导弹的操稳性来满足20g的过载要求。
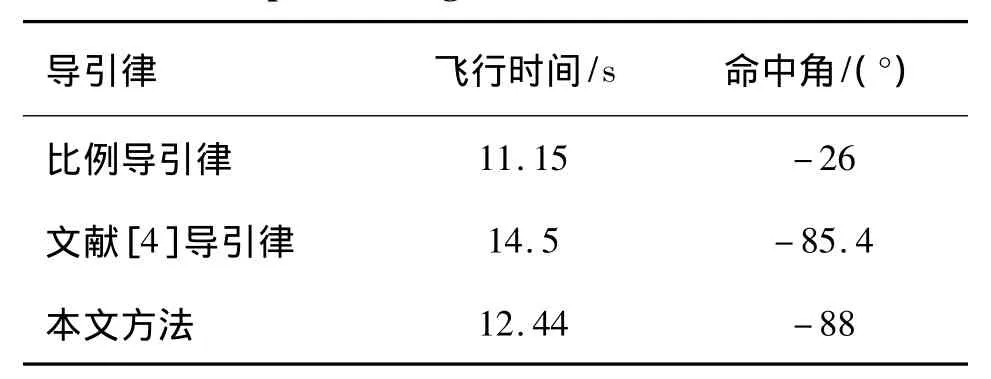
表1 不同导引律仿真对比结果Table 1 Comparison of guidance laws simulation results

图4 2种导引律过载对比Fig.4 Comparison of guidance laws overload

图5 改进前后剩余时间对比Fig.5 Com parison of time-to-go estimation
(2)情况二
要求单架无人机从不同地点、不同时刻发射多枚导弹,要求同时到达目标。确定各期望命中时间tf时,必须大于在各个距离上最小飞行时间。无人机从坐标(0,1 000,0)以速度vm=100 m/s沿正X方向飞行,目标位置在(2 600,0,1 000),单位m。无人机每隔2 s发射1枚导弹,共发射3枚,要求在第1枚发射后15 s所有导弹都命中目标,也就是要求每枚导弹飞行时间分别为tf=11、13、15 s,导弹初始条件和导引律的各项比例系数的取值与情况一相同。
情况二仿真结果见表2。情况二仿真弹道见图6,情况二过载见图7,情况二剩余时间估计比较见图8。
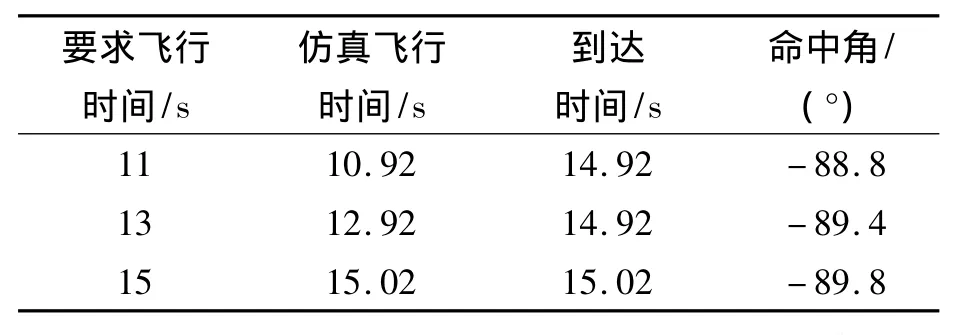
表2 情况二仿真结果Table 2 Simulation results of case 2

图6 情况二仿真弹道Fig.6 Trajectories of case 2
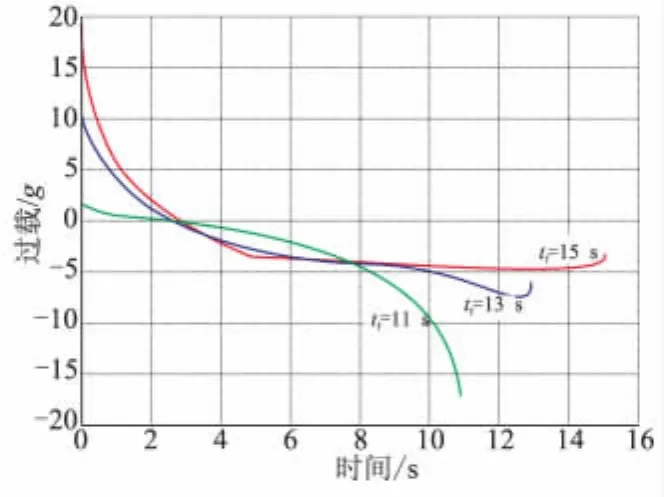
图7 情况二过载Fig.7 Overload of case 2
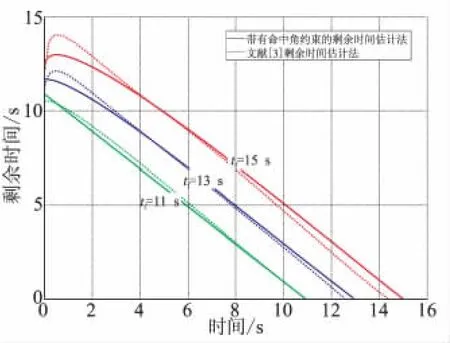
图8 情况二剩余时间估计比较Fig.8 Com parison of tim e-to-go estimate of case 2
从仿真结果可知,当时间为15 s时,比在此位置比例导引法的需用时间大得多,弹道会有较大的上升过程,因此此时的初始过载就较大。随着时间接近比例导引法的需用时间,弹道的上升过程缩短,初始过载随之变小,末端过载随之加大,所以确定期望命中时间时,也要考虑导弹可用过载的限制;命中角也几乎控制为-90°,可实现攻顶;剩余时间也几乎成线性,表明采用的剩余时间估计方法较有效;可看出,考虑了命中角约束的剩余时间估计法,比文献[3]中的估计方法更适合同时带有命中角约束的导引方法。随着期望命中时间的增加,在该方法控制下的导弹飞行时间更接近期望命中时间,可较准确地保证3枚导弹同时到达目标。
5 结束语
仿真结果证明,通过加入了考虑了命中角约束的剩余时间估计方法,使在这种控制命中角和命中时间的修正比例导引律导引下的无人机机载小型导弹,以更为准确的命中时间、接近垂直的命中角,命中地面或海面的固定或低速运动目标。
[1] Jeon IS,Lee J I and Tahk M J.Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology,2006,14(2):260-266.
[2] Ryoo C K,Cho H Jand Tahk M J.Closed-form solutions of optimal guidance with terminal impactangle constraint[C]//The IEEE Int'l Conference on Control Application,June 23-25,2003.
[3] Jung B Y,Kim Y D.Guidance laws for anti-shipmissiles using impact angle and impact time[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,Keystone,Colorado,USA,August21-24,2006.
[4] 杨俊鹏,祝小平,周洲.电视制导无人机导引律研究[J].西北工业大学学报,2005,23(4):479-482.

