有斜桩和无斜桩高桩码头地震反应的非线性有限元分析
李 颖,贡金鑫
(大连理工大学 结构工程研究所,辽宁 大连 116024)
高桩码头结构常采用斜桩来抵抗各种水平荷载,如船舶系缆力、撞击力及地震荷载等.因为斜桩能够通过受压提供水平承载力.事实上,带有斜桩的高桩码头在承受船舶停泊、靠岸和装卸操作产生的侧向荷载方面表现出良好的性能.但在地震作用下,带有斜桩的高桩码头表现并不尽人意.例如,1995年日本兵库县南部地震中,神户港斜桩式高桩码头的受灾主要由基础地基和墙后地基液化引起的侧向荷载所造成的,造成上部结构的振动,直至破坏.1989年美国Loma Prieta地震时奥克兰港Ben Nutter码头的几百根斜桩遭受严重破坏,桩板连接处受到很大拉力,导致混凝土破裂和钢筋裸露,港口关闭数月以进行修复[1].1995年美国曼萨尼约港高桩码头13号泊位的斜桩体系在地震中也遭受严重地震破坏,顶部有372根混凝土直桩和斜桩,面板拱腹附近约有300根桩出现大裂缝和脱落现象.尽管码头外侧使用了斜桩,但是由于围堰过于陡峭,致使剪切荷载集中作用在斜桩上,直到地震后2年半,13号泊位的码头结构才完全修复[2].在2004年苏门答腊地震中,Sagar Dweep靠泊码头的斜桩和桩-面板连接处在地震产生的巨大轴力下发生破坏,而直桩虽然因弯曲而受到损坏,但易于修复[3].根据1976年唐山地震震害调查,天津塘沽新河外运码头横向的13对叉桩全部破坏,近陆侧斜桩有的被拉断,有的把桩帽拉下一半后倒向水中.近海侧斜桩受到强大推力,桩的斜度变陡,桩顶升高,把面板顶起,桩身上部1 m范围内的混凝土均被压碎;桩身其余部分也大都劈裂.码头斜桩的破坏率为100%,而在119根直桩中,破坏的只有37根,破坏率为31.9%.在斜桩位置处的码头面板向上拱起,并产生贯穿整个面板的纵向裂缝[4].我国沿海港口地区至今没有遭受过强烈的地震作用,因此高桩码头抗震设计经验积累相对较少.本文采用非线性有限元方法分析讨论地震作用下有斜桩和无斜桩高桩码头的性能.
1 高桩码头的非线性有限元分析方法
高桩码头是由面板、梁、桩和土组成的结构体系,在这种结构形式中,准确反映土-结构的相互作用非常重要.一些学者曾采用有限元和试验方法针对斜桩对高桩码头抗震性能的影响进行了研究[5-7].有限元方法的基本思路是,根据总势能最小原理导出表示结点力和结点位移关系的单元刚度矩阵,然后将单元刚度矩阵进行叠加,形成系统的总刚度矩阵,集成整个结构的综合等效结点荷载列阵后,求解建立在整体刚度矩阵上的联立方程组,得到每个结点的位移,然后便可以确定每个单元的应力和应变.而非线性有限元方法则根据非线性应力-应变关系,把它逐段转化为一系列线性问题,用迭代法求解.导致非线性的原因主要是材料非线性和几何非线性.材料非线性是本构关系的非线性,它引起整个问题的非线性;而几何非线性的特点是结构在荷载作用过程中产生大位移和转动,例如大挠度、屈曲等.本文采用非线性有限元软件ABAQUS计算地震作用下全直桩和有斜桩高桩码头的地震反应.
1.1 混凝土本构模型
在强烈地震作用下,高桩码头的混凝土会进入非线性状态,这种状态可采用混凝土的本构模型描述.ABAQUS常用的混凝土本构模型包括弥散开裂模型和塑性损伤模型.本文中码头桩基与面板混凝土采用塑性损伤模型[8]模拟,该模型考虑了材料拉压性能的差别,可模拟损伤引起的不可恢复材料性能退化.该模型假定混凝土材料的破坏主要为拉裂和压碎,屈服和破坏面的演化由拉伸等效塑性应变和压缩等效塑性应变控制.下式为J.Lee提出的适合于模拟反复荷载下混凝土力学性能的屈服函数[9]:
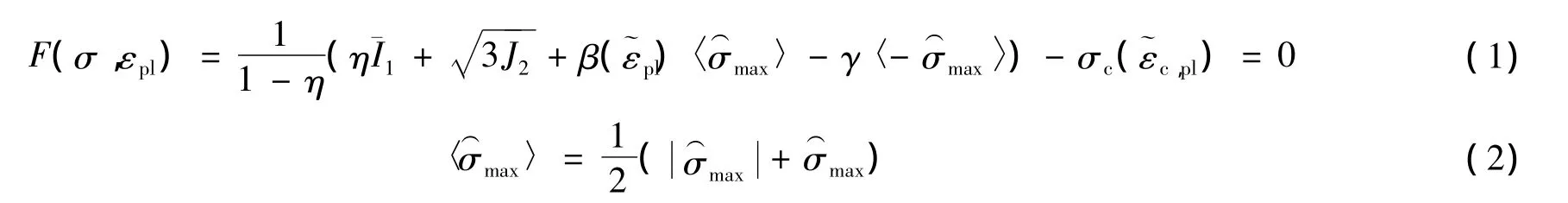
1.2 钢筋本构模型
钢筋的应力-应变模型有多种[10],不同模型需要不同参数.ABAQUS中定义塑性数据时,采用真实应力和真实塑性应变.本文有限元模型定义钢筋时,采用单元截面定义配筋层(Rebar layer)的方法,选用标准金属塑性模型描述钢筋塑性性能,采用Embedded region命令使其耦合在混凝土桩内,以此将钢筋单元叠加于模拟混凝土单元网格上.对于预应力钢筋单元,预应力是通过Initial condition定义有效预应力变化建立的.
1.3 桩土界面模型
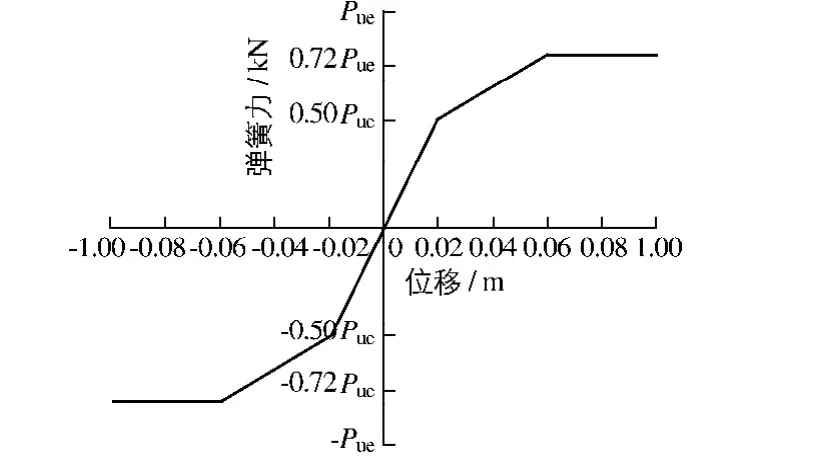
图1 桩侧法向土弹簧力-位移关系Fig.1 Force-displacement curve of soil
桩土相互作用是高桩码头地震作用下的重要特征.常用的桩土接触模型包括Goodman单元法[11]和Winkler地基梁模型等.本文在桩土界面上采用了p-y曲线法,假设土体在任意点的反力只与该点的位移成正比,桩周土体用彼此相互独立分布的一组弹簧和阻尼器代替,以综合反映桩周土的非线性、桩的刚度和外荷载等特点.划分桩体单元后,将非线性弹簧加在土中桩段单元的节点上,并输入单元的力-位移曲线.根据ABAQUS土弹簧单元的性质,需要确定土反力p与桩身位移y的对应关系.参考文献[12],某深度处的桩侧法向土弹簧力-位移关系如图1所示,Pue为侧向土弹簧的屈服力,Pue=Pu×le×b;Pu为单位面积上的极限土阻力,le,b分别为桩的单元长度和宽度.确定土弹簧单元刚度时首先确定某深度处黏性土桩侧法向单位面积的极限土阻力Pu和标准p-y曲线,并根据p-y曲线向ABAQUS输入非线性力-位移曲线.
1.4 解动力平衡方程的隐式积分法
高桩码头-土动力相互作用系统的动力平衡方程为

式中:M为n×n的质量矩阵;C为n×n的阻尼矩阵;K为n×n的刚度矩阵为体系输入的地震加速度时程;u为n×1的结构相对位移向量;I为惯性力指示向量.
引入控制积分稳定性的参数α,式(3)改写为:

式中:L为与自由度有关的拉格朗日因子力之和.
动力时程分析法是通过逐步积分求解系统运动方程的,本文采用Newmark隐式积分法.该方法是一种将线性加速度法普遍化的方法,某一时刻的位移和速度可表示为
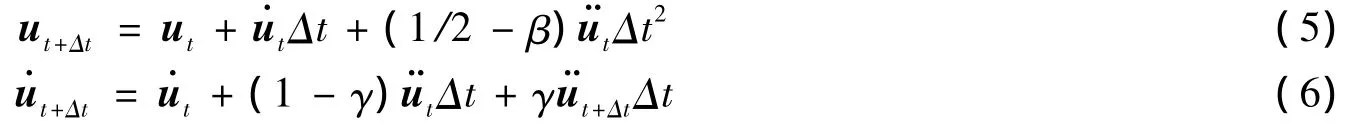
上述积分方法是无条件稳定的,当α=0时,称为Newmark-β法.当采用自动计算时间步长调整时,时间步长的变化往往会对积分计算的稳定性和收敛性产生影响,采用微小的数值阻尼可消除这种影响.这种数值阻尼通过参数α取非零值提供,一般的土-结构动力相互作用分析中取α=-0.05即能基本满足上述要求,同时对低频反应的影响甚小,当α取值太小时,会引起过阻尼现象.
隐式积分法求解动力问题时需要自动计算时间步长,是通过在半积分时间步长时对体系最小结点残差力的大小来调整的.假设加速度值在任一时间步长内线性变化,则
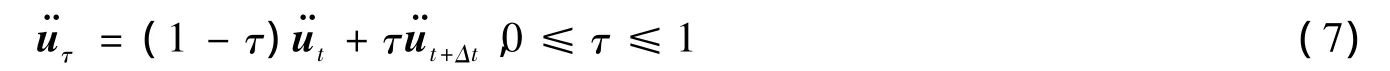
式中:τ为时间步长内的任一时刻.利用式(5),(6)和(7)可求出某点在某一时间步长内任一时刻的位移、速度和加速度值,即

为分析有斜桩码头与无斜桩码头的地震反应,本文分别对码头结构水平承载力不同和水平承载力相近的情况进行了对比分析.
2 计算条件与模型
2.1 码头结构形式
图2为本文研究的3个深水港预应力高桩码头结构的断面图.图2(a)为全直桩码头,桩台宽22.5m,桩排架间距4.4 m,每一结构段由12~13榀排架构成;桩台面板、路面及磨耗层厚度为400mm.全直桩结构桩台下有6根基桩,每根长25.25m,为550mm×550mm的方形截面.图2(b)为有斜桩的码头,即在上述全直桩结构的基础上在近海侧第3根直桩处添加2根截面尺寸为550mm×550mm的斜桩,本文中将这种结构简称为斜桩码头,斜桩长26m,倾斜度为3∶1,桩内对称布置2Φ8的冷拉Ⅲ级钢筋和8Φ28的普通低碳钢筋.图2(c)同样为在全直桩码头的基础上增加1对斜桩,但直桩的桩身截面尺寸减小为500mm×500mm,配置1Φ8的冷拉Ⅲ级钢筋和4Φ24的普通低碳钢筋,本文简称为新斜桩码头.码头中的直桩自左向右编号依次为1#~6#,斜桩依次为7#~8#.
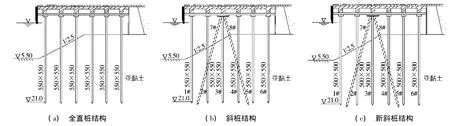
图2 预应力高桩码头断面Fig.2 Cross section of wharf structure
2.2 材料和岩土参数
码头结构混凝土的强度等级均为C40,图3为C40混凝土应力应变关系曲线,混凝土弹性模量为3.3×104MPa,泊松比为0.15,密度为2500kg/m3.桩中预应力钢筋采用冷拉Ⅲ级钢筋,屈服强度为1450mPa,张拉后初始应力为1000mPa,弹性模量为2.05×105MPa,图4为预应力钢筋及普通钢筋的应力应变关系.普通低碳钢筋对称布置,弹性模量为2.1×105MPa,泊松比为0.3,密度为7850kg/m3.
建设场地内是地质年代为第四纪全新世的新鲜土层,含水量较高,为计算简便本文将场地土简化为一层淤泥质亚黏土,其有效重度为19.70 kN/m3,含水量为32.2%,摩擦角为20°,黏聚力为23 kPa.按上述参数计算土弹簧非线性力-位移曲线如图5所示,图中“○”处为输入的常数,单元长度设置为1.0m.
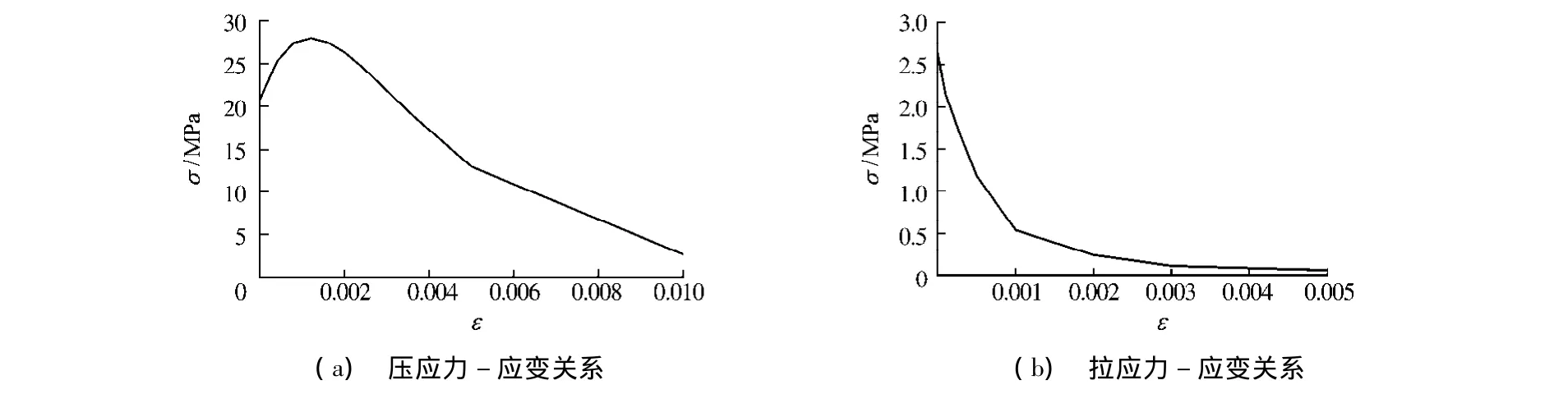
图3 C40混凝土的应力应变关系Fig.3 Stress-strain curves of C40 concrete in compression and tension
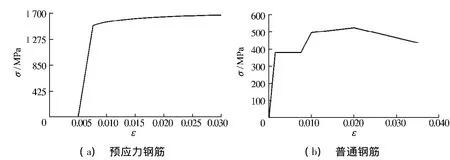
图4 预应力钢筋和普通钢筋的应力应变关系Fig.4 Stress-strain curves of prestressed tendon and reinforcement
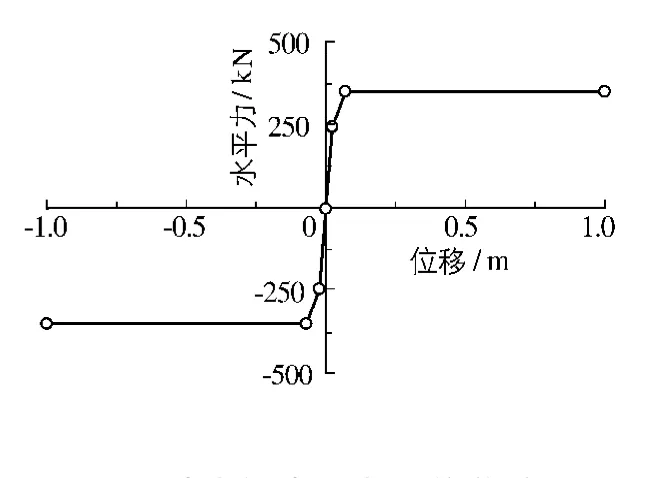
图5 场地土的水平力-位移关系Fig.5 Horizontal force-displacement curve of site soil
2.3 有限元模型的建立
假定地震水平作用于码头,由于结构和荷载的对称性,取典型的4.4 m排架进行计算.图6为建立的全直桩码头和斜桩码头结构的三维有限元模型,桩和面板均采用空间八节点单元,全直桩码头有1026个单元,有斜桩的码头有1559个单元.
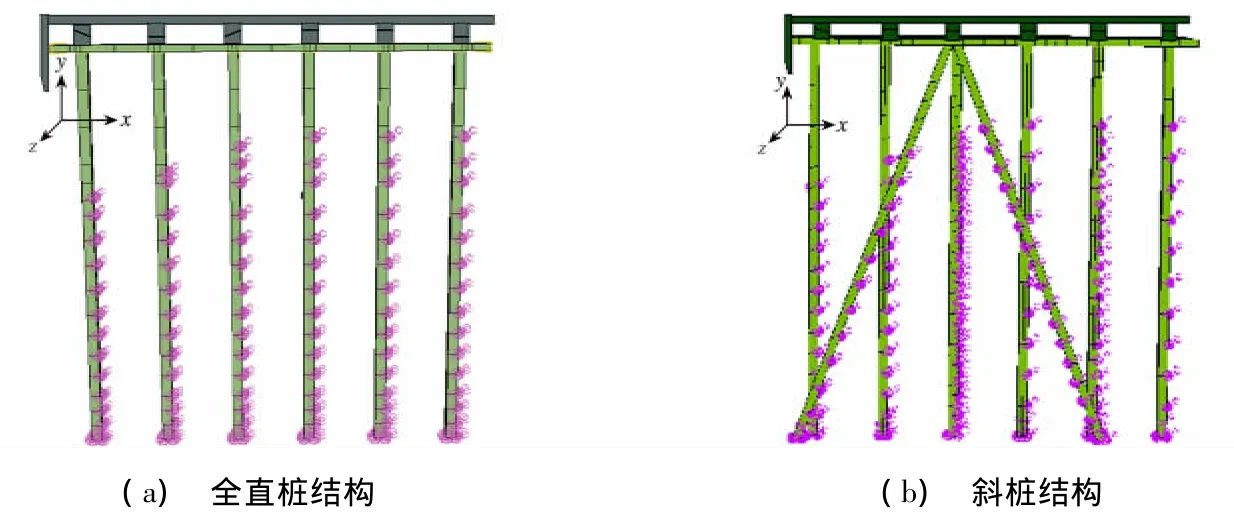
图6 高桩码头有限元模型Fig.6 Finite element model of wharves
为了解高桩码头结构在水平荷载作用下的荷载-位移特性,在码头面板处施加不断增大的水平荷载,利用ABAQUS进行静力分析得到码头结构的水平荷载-位移曲线(见图7).由图可见,新斜桩码头水平荷载下的荷载-位移曲线与全直桩码头相近.随着水平荷载的增加,全直桩码头的位移平稳增大,变形性能较好,刚度较低;而斜桩码头的弹性刚度较大,当荷载约为1200 kN时,曲线发生明显的转折,可能是斜桩发生了受压破坏,承载力降低.总体来讲,与全直桩码头相比,斜桩码头水平刚度较大,位移较小,而新斜桩码头刚度与全直桩码头刚度相近,略微偏大.需要说明的是,这里对直桩码头、斜桩码头和新斜桩码头施加水平力进行推覆分析是为了了解3种码头的水平位移特性,新斜桩码头与全直桩码头刚度相近也是专门设计的,与采用Pushover方法分析码头的变形不同,因为计算中没有规定地震的强度和采用的反应谱.采用Pushover方法分析码头变形的研究可参见文献[13].
2.4 荷 载 条 件
本文非线性时程分析输入的地震波分别为Northridge和El Centro地震波(见图8),其峰值加速度分别为 0.8427g 和0.3569g(g=9.81 m/s2),持续时间均取 30 s.
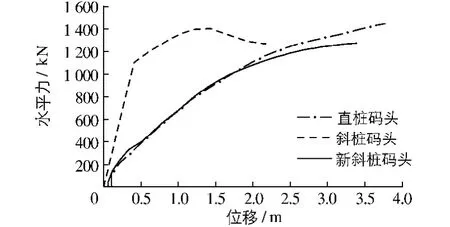
图7 3种码头的荷载-位移曲线Fig.7 Load-displacement curves of three wharf structures
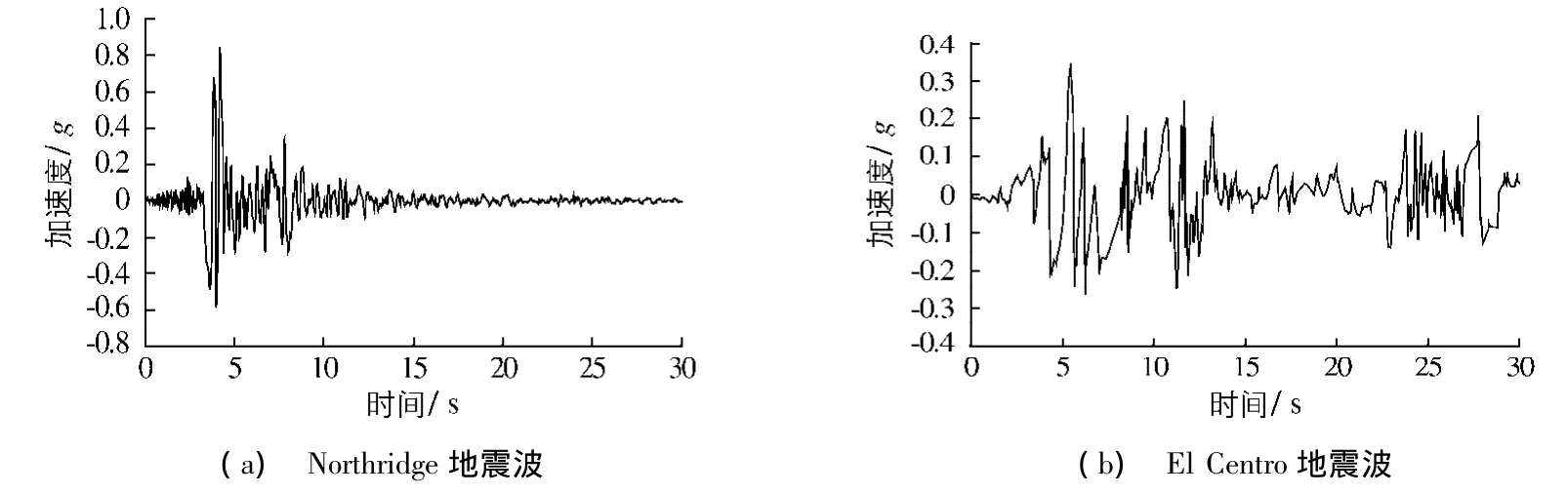
图8 Northridge地震波和El Centro地震波时程曲线Fig.8 Time-history curves of Northridge motion and El Centro motion
简单来看,2种地震波的区别是,Northridge波的强震阶段在3~8 s,之后明显衰减;El Centro波在3~13 s属于强震,之后有所衰减,在26~30 s间又出现次强震.为了反映不同强度地震水平下高桩码头的动力反应,将地震峰值加速度按比例缩放为0.1g,0.2g和0.4g,分别对应于建筑抗震规范的7度、8度和9度地震.
3 计算结果分析
3.1 自振频率和周期
为了解3种码头结构的自振特性,采用ABAQUS中的Lanczos方法分别提取了3种码头的前5阶固有频率(见表1).可以看出,斜桩码头的自振频率大于全直桩码头,即斜桩码头的自振周期小于全直桩码头的,显然这是因为斜桩码头的刚度大于全直桩码头刚度的缘故.
对于新斜桩码头,尽管已对其截面尺寸和配筋进行调整,使其在水平荷载作用下的变形特性与直桩码头接近,但调整后的新斜桩码头自振频率仍大于全直桩码头.这是因为使2种码头的水平荷载-变形特性接近是在整个弹塑性阶段考察的,而计算的自振频率是针对弹性阶段的,所以2种码头弹性阶段的特性仍有一定差别.

表1 结构自振特性Tab.1 Natural characteristic of wharf structures
3.2 水 平 位 移
图9和10为Northridge和El Centro地震波条件下3种高桩码头面板的水平位移时程曲线,表2为地震后3种码头的水平残余位移.可见,随着地震峰值加速度的增大,码头的水平位移增大.
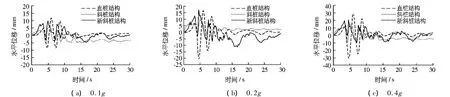
图9 Northridge地震波条件下3种码头面板的水平位移时程曲线Fig.9 Horizontal displacement history for decks under Northridge motion
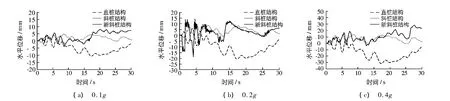
图10 El Centro地震波条件下3种码头面板的水平位移时程曲线Fig.10 Horizontal displacement history for decks under El Centro motion
在同一地震水平下,与直桩码头相比,2种斜桩码头面板的水平位移均大大减小.由表2可以看出,2种斜桩码头的残余位移均比全直桩码头大,这表明:(1)全直桩码头增加一对斜桩后,虽然码头刚度增大,地震过程中的水平位移减小,但结构残余位移却增大,使其震后修复过程变得更加困难;(2)而在水平承载力接近的情况下,码头结构采用斜桩抵抗地震并不是好的方法.
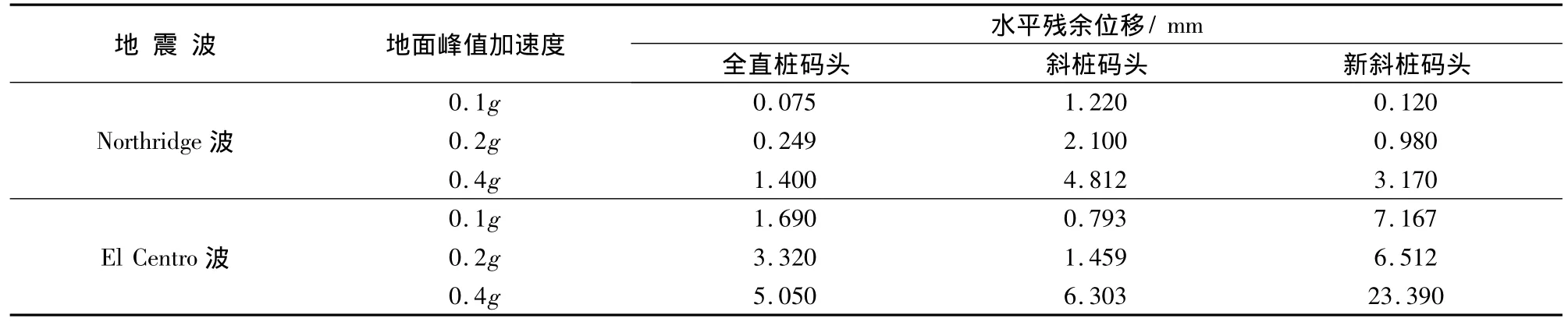
表2 3种高桩码头的水平残余位移Tab.2 Horizontal residual displacement of three wharf structures
3.3 桩顶水平力
图11为0.2g和0.4gNorthridge地震波下3种高桩码头各桩桩顶水平力的时程曲线,图12为0.2g和0.4gEl Centro地震波下3种高桩码头桩顶水平力的时程曲线.可以看出,在2种地震波下,斜桩码头的5#桩在地震开始一段时间后水平力不再变化,且承受的水平力比斜桩还大,与全直桩码头5#桩的最大水平力接近.由此可见,尽管设置斜桩确实使很多桩的水平力大大减小,但也使码头的地震反应变得复杂,有些桩的水平力并没有降低.
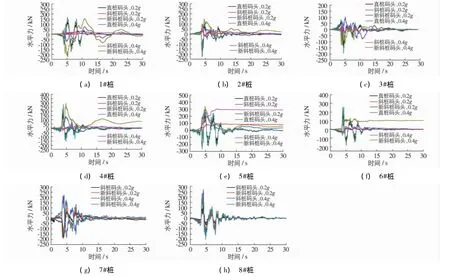
图11 Northridge地震波下3种码头结构桩顶水平力时程曲线Fig.11 Horizontal forces at pile heads of wharf structures under Northridge motion

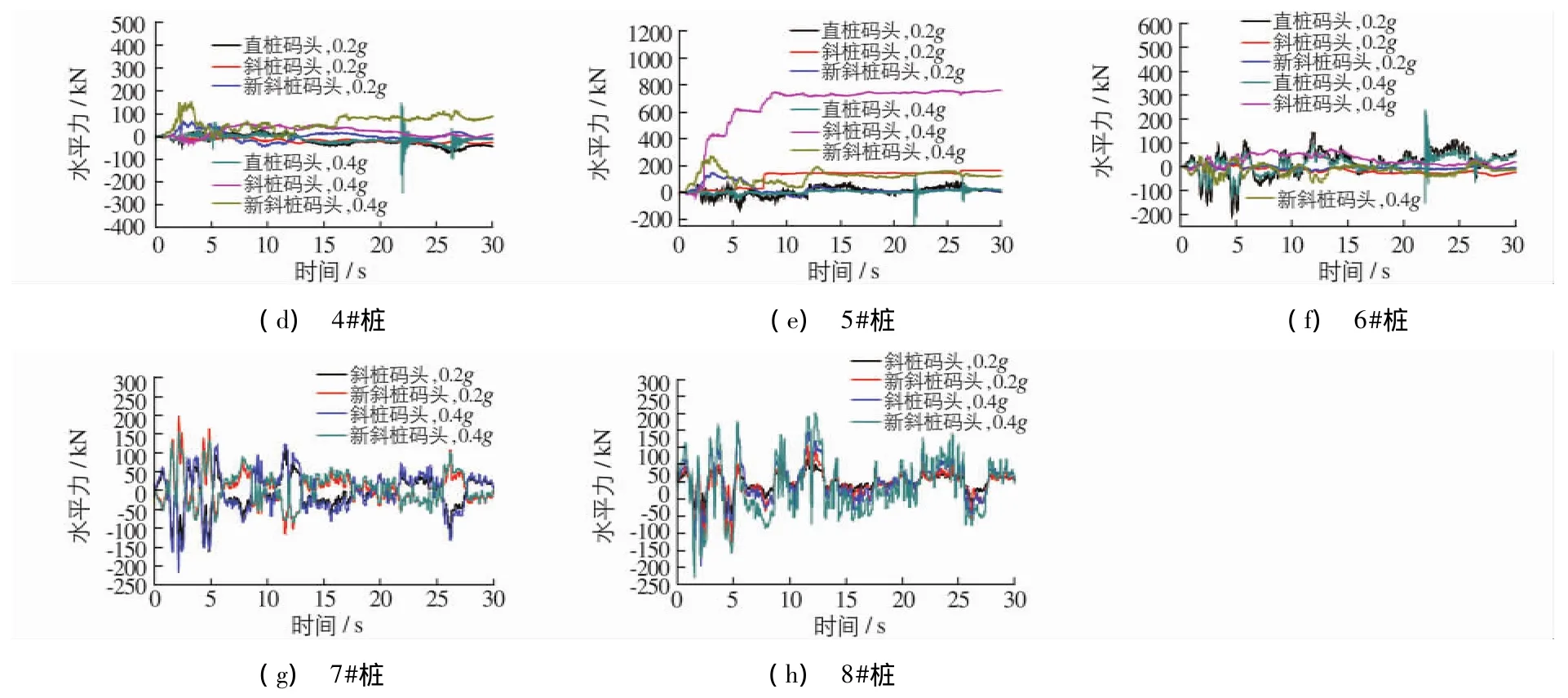
图12 El Centro地震波下3种码头结构桩顶水平力时程曲线Fig.12 Horizontal forces at pile heads of wharf structures under El Centro motion
表3为直桩码头和斜桩码头及新斜桩码头桩顶水平力最大值.可见,随着地面峰值加速度增大,码头结构水平侧向力随之增加.与两种斜桩码头结构相比,全直桩码头同一根桩承受的水平荷载要大;近陆桩承受的水平荷载比近海桩的大,成为承担水平地震荷载的主要构件,这符合1989年Loma Prieta地震中美国奥克兰港第七街码头观测到的震后损坏情况(95%的近陆侧桩和50%近海侧桩严重破坏).这是因为近陆侧斜桩暴露在空气中的长度小,刚度要大,需要承受更多的水平荷载和惯性土压力.由此可以看出,强震中高桩码头中承担主要地震水平力的是近陆侧直桩,因此设计近陆侧桩时需要考虑增加其水平抵抗能力,而不是仅仅承担结构重量.由于近陆桩外露长度短而承担的水平力大,容易形成短柱,发生剪切破坏,而我国水运工程抗震规范中没有关于地震作用下桩受剪承载力的计算方法,需要进行研究.

表3 全直桩码头和斜桩码头桩顶最大水平力Tab.3 Peak horizontal forces at pile heads of plumb and batter pile system
3.4 桩顶轴力和弯矩
图13为0.2g和0.4gNorthridge地震波下3种码头结构各桩的桩顶弯矩时程,0.2g和0.4gEl Centro地震波下3种码头结构各桩的桩顶弯矩时程见图14.从图可以看出,码头结构各桩桩顶弯矩随着地震波峰值加速度增加而增加.在Northridge地震波作用下,全直桩码头的振动比较有规律,形似衰减的正弦波,而斜桩码头振动的规律性比较差.这是因为斜桩分担了直桩的水平力;如新斜桩码头的近海侧斜桩7#桩在震动过程中及震后一直保持很大的残余弯矩.而在El Centro地震波作用下,全直桩码头的残余弯矩比较大.因为全直桩结构钢筋屈服后桩处于塑性状态,地震结束后码头回到原位,必然会存在很大的残余弯矩.图15为0.4g El Centro地震波下直桩码头和新斜桩码头各桩桩顶轴力的时程曲线.由图可见,地震过程中新斜桩码头比直桩码头承受的轴力大.

图13 Northridge地震波下3种码头结构各桩桩顶弯矩的时程曲线Fig.13 Dynamics moment at pile heads of wharf structures under Northridge motion
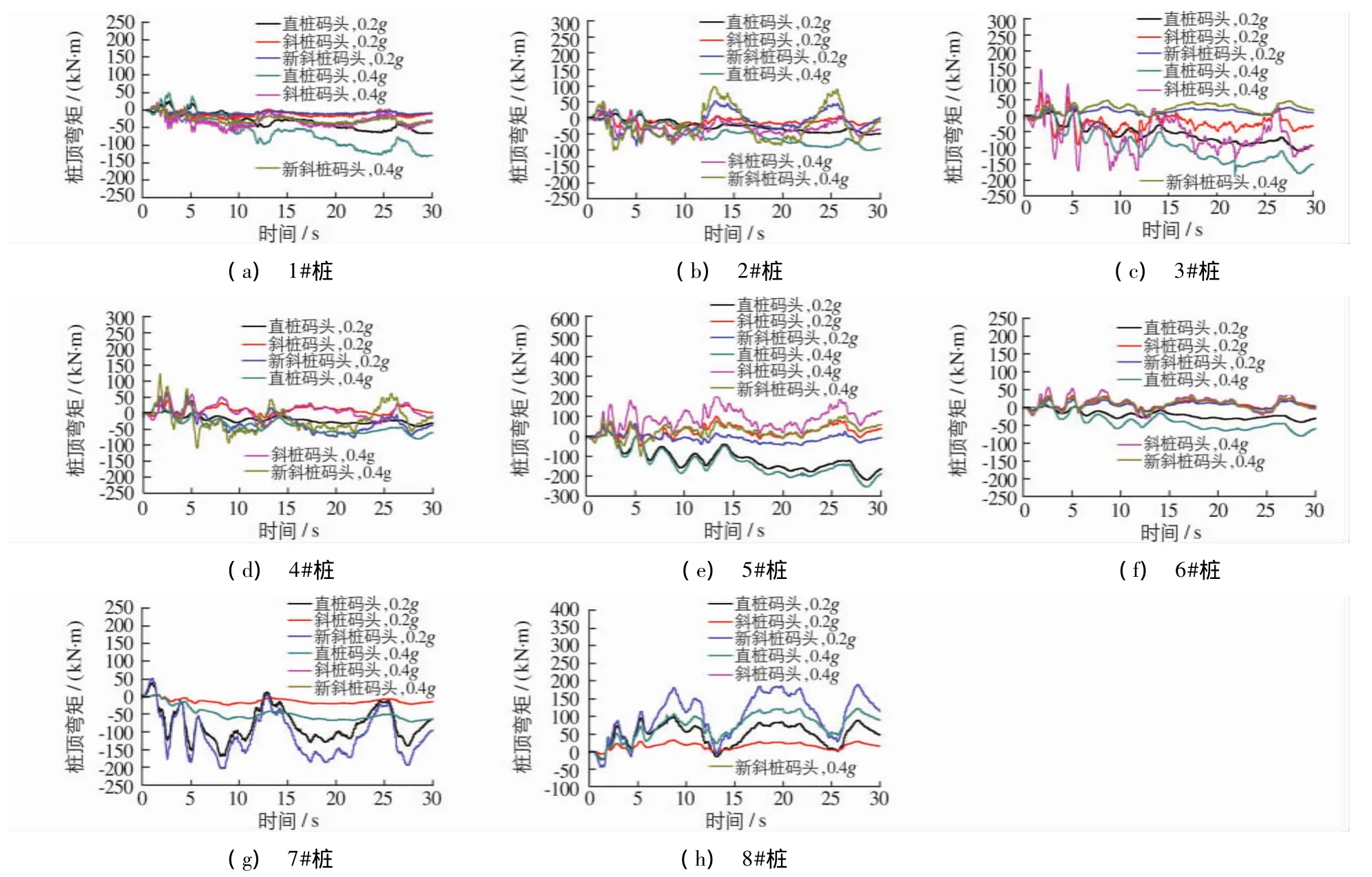
图14 El Centro地震波下3种码头结构各桩桩顶弯矩的时程曲线Fig.14 Dynamics moment at pile heads of wharf structures under El centro motion
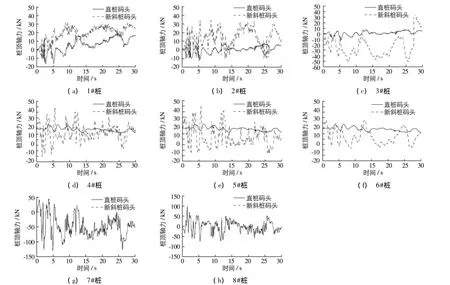
图15 0.4g El Centro地震波下直桩码头和新斜桩码头各桩桩顶轴力的时程曲线Fig.15 Axial force at pile heads of plumb and new batter wharf structures under El Centro motion with PGA of 0.4g
钢筋混凝土桩属于偏心受压或受拉构件,其承载力存在轴力和弯矩的耦合作用,即在不同的轴力下桩承受的弯矩是不同的,图16(a)所示为新斜桩码头桩的轴力(拉为正,压为负)-弯矩相关曲线,图16(b)~(i)示出了30 s的0.4g El Centro地震波作用下各桩不同时刻实际承受的轴力-弯矩组合,同时也示出了桩的轴力-弯矩相关曲线.需要说明的是,由于各桩的轴力不是很大,如果按图16(a)的比例在图16(b)~(i)中全部画出桩的轴力-弯矩相关曲线,则桩实际承受的轴力-弯矩组合点不能够看清楚,为此图16(b)~(i)中只画出了桩的轴力-弯矩相关曲线的一部分.从图16(b)~(i)可以看出,对于新斜桩码头,在30 s的0.4g El Centro地震波的作用下,4#桩、5#桩和7#桩的有些轴力-弯矩组合点落在轴力-弯矩相关曲线的边界上(实际上由于按单桩计算的轴力-弯矩相关曲线与码头中桩的轴力-弯矩相关曲线略有差别,一些轴力-弯矩组合点稍微超出了轴力-弯矩相关曲线),说明地震过程中这些桩达到了极限承载力,有可能发生破坏.其他桩的轴力-弯矩组合点落在轴力-弯矩相关曲线内部,没有达到极限承载力,未发生破坏.
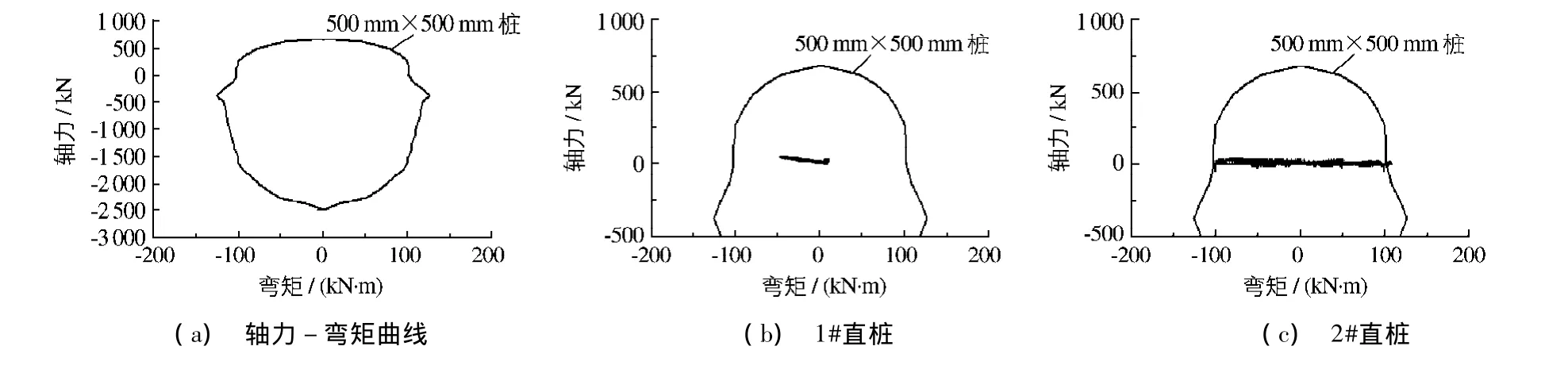
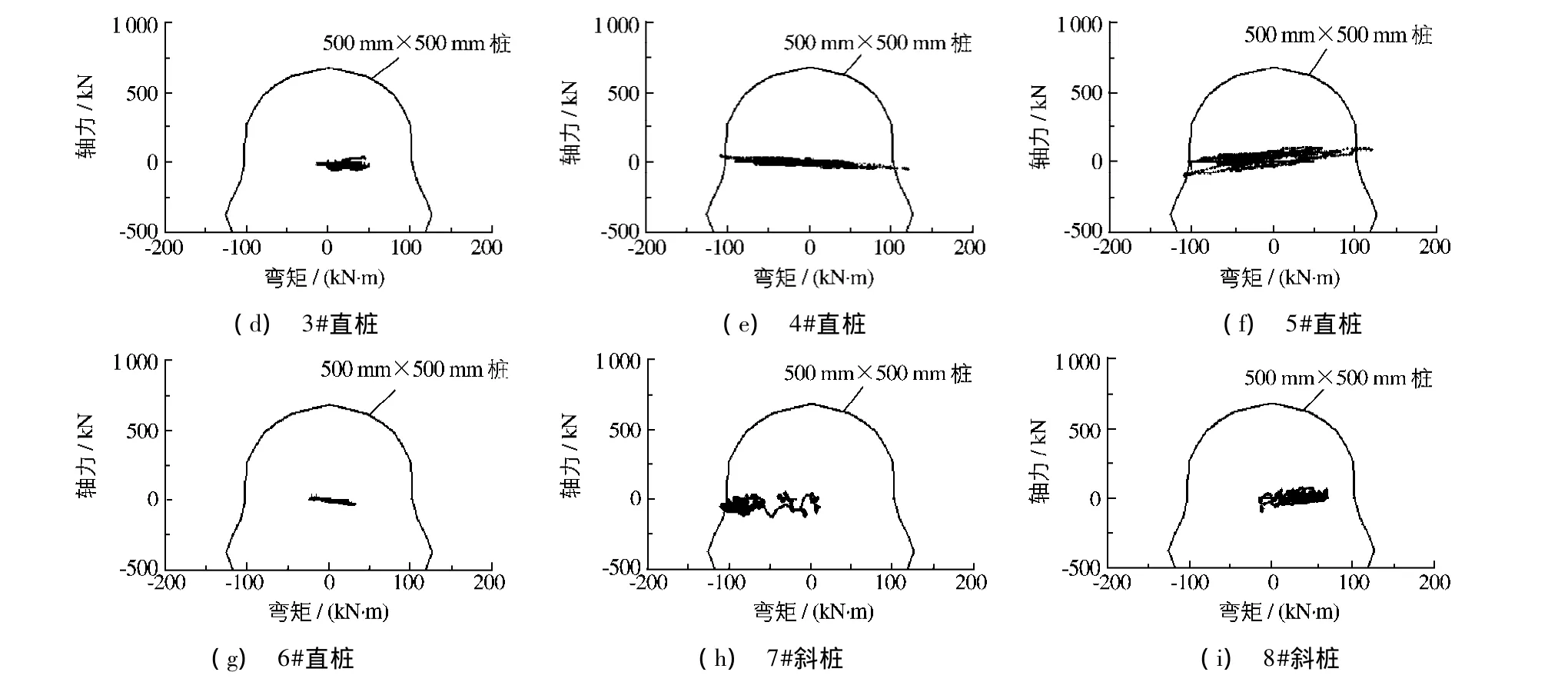
图16 El Centro 0.4g地震波下新斜桩码头各桩桩顶与抵抗弯矩的比较Fig.16 Comparison with resistance moment at pile heads of new wharf structures under El Centro motion with PGA of 0.4g
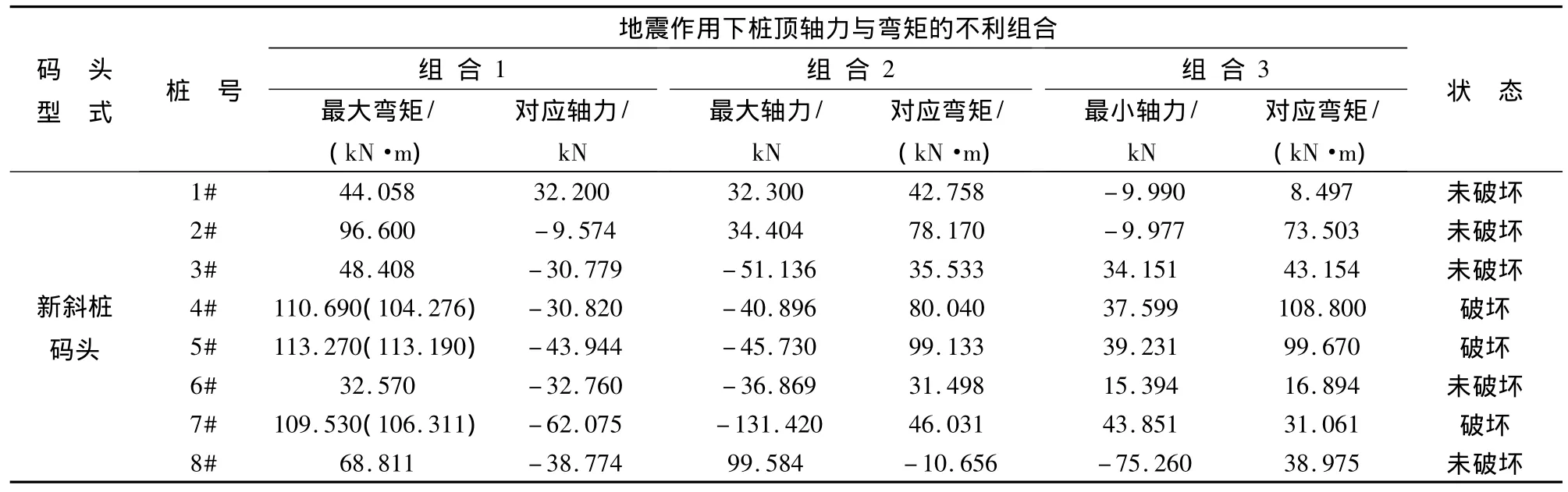
上面是根据地震过程中桩轴力-弯矩组合点与轴力-弯矩相关曲线的关系判断桩的状态的,工程设计中不需要对所有的轴力-弯矩组合点进行判断,而是根据起控制作用的轴力-弯矩组合进行分析.根据钢筋混凝土偏心受压构件的破坏特点,常用的组合有:(1)最大弯矩+对应的轴力,(2)最大轴力+对应的弯矩,(3)最小轴力+对应的弯矩.表4为0.4g El Centro地震波条件下直桩码头和新斜桩码头各桩的3种组合.计算表明,对于新斜桩码头的4#桩、5#桩和7#桩,按组合(1)弯矩均超过了桩的承载力,因而可以断定地震过程中这3根桩发生了破坏,与前面的结果相同.图17为按组合(1)的轴力对新斜桩码头的4#桩、5#桩和7#桩进行推覆得到的弯矩-位移曲线,曲线的最高点对应为该轴力下桩可承受的最大弯矩,即表4中括号中的值.

图17 单桩轴力作用下的弯矩-位移曲线Fig.17 Moment-displacement curve for piles under axial force

表4 0.4g El Centro地震波下码头的抵抗弯矩Tab.4 Resistance moment at pile heads under El Centro with PGA of 0.4g
(续表)
3.5 桩顶混凝土应变
通过查看桩顶混凝土压应变,可以判断地震作用下高桩码头的桩是否已经发生压碎破坏.图3给出了C40混凝土的压应力-应变曲线,该曲线表示混凝土压应变超过约0.0017后,混凝土开始软化,承载力下降,但并不意味着混凝土已经完全破坏.按照混凝土规范的规定,工程上认为混凝土被压碎的应变为0.0033.图18为El Centro地震作用下全直桩码头和新斜桩码头桩顶的压应变时程曲线.可以看出,新斜桩码头5#和7#桩的压应变超过0.0033,因此可以判断5#桩和7#桩桩顶混凝土发生了压碎破坏;而全直桩码头各桩压应变均未超过0.0033,所以可认为全直桩混凝土未发生破坏.

图18 El Centro地震作用下码头桩顶的压应变时程曲线Fig.18 Strain in compression at pile heads under El Centro motion
4 结语
通过非线性有限元计算分析,对全直桩码头和2种斜桩码头结构进行了地震反应研究.研究得出如下主要结论:
(1)在同一地震作用下,与全直桩码头相比,斜桩码头的水平位移较小,同一直桩承受的弯矩、水平侧向力均较小,但有时会有较大的残余位移.
(2)对于水平承载力-变形特性与全直桩码头相近的新斜桩码头,在同一地震作用下,新斜桩码头的水平位移,以及同一直桩承受的弯矩和水平侧向力都偏小,但比不削弱直桩截面的斜桩码头大,而且新斜桩码头残余位移更大,斜桩更容易发生破坏.因此使用斜桩会增加码头结构的地震反应复杂性.
(3)使用斜桩虽然降低了直桩承受的水平力,但使码头结构的地震反应变得更为复杂,当地震作用较强时,其自身却容易发生破坏,一方面失去了水平承载力,另一方面则引起较大残余位移,不利于修复.因此在强地震区内设计高桩码头结构选择斜桩时更需谨慎.
[1]SCHLECHTER S M,DICKENSON S E,MCCULLOUGH N J,et al.Influence of batter piles on the dynamic behavior of pile-supported wharf structures[C]∥Proceedings of the Ports 2004 Conference,Houston:Texas,2004:420-430.
[2]BARDI J C,RUIZ G P,KUMAR V K.Manzanillo Mexico's SSAMM Terminal:Lessons learned from 1995 and 2003 earthquakes[C]∥Proceedings of the Ports 2004 Conference,Houston:Texas,2004:25-31.
[3]MONDAL G,RAI D C.Performance of harbour structures in Andaman Islands during 2004 Sumatra earthquake[J].Engineering Structures,2008(30):174-182.
[4]刘恢先.唐山地震[M].北京:地震出版社,1986.(LIU Hui-xian.Tangshan earthquake[M].Beijing:Earthquake Publish Company,1986.(in Chinese))
[5]MAGEAU D W,CHIN K H.Finite element modeling of new marine terminal at the port of Tacoma[C]∥Proceedings of the Ports 2007 Conference:30 Years of Sharing Ideas,USA,2004.
[6]龙炳煌,雷立志.高桩码头叉桩震害分析及设计建议[J].中国港湾建设,2007(1):7-10.(LONG Bing-huang,LEI Lizhi.Seismic analysis and design suggestions batter-piles in pile-wharfs[J].China Harbour Engineering,2007(1):7-10.(in Chinese))
[7]李颖,贡金鑫.考虑桩土相互作用的高桩码头非线性地震反应分析[J].水利水运工程学报,2010(2):92-99.(LI Ying,GONG Jin-xin.Nonlinear seismic response analysis of wharf structure considering soil-pile dynamic interaction[J].Hydro-Science and Engineering,2010(2):92-99.(in Chinese))
[8]LEE J,FENVES G L.Plastic-damage model for cyclic loading of concrete structures[J].Journal of Engineering Mechanics,1998(4):892-900.
[9]Analysis user's manual of ABAQUS 6.6.Volume Ⅲ:Materials[M].American ABAQUS Inc,2006.
[10]过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003.(GUO Zhen-hai,SHI Xu-dong.Reinforced concrete theory and analyses[M].Beijing:Tsinghua University Press,2003.(in Chinese))
[11]GOODMAN R E,TAYLOR R L,BREKKE T L.A model for the mechanics of jointed rock[J].Journal of Soil Mechanics and Foundations Div,1968,94(3):637-659.
[12]杨克己.实用桩基工程[M].北京:人民交通出版社,2004.(YANG Ke-ji.Practical engineering of pile foundations[M].Beijing:China Communications Press,2004.(in Chinese))
[13]李颖,贡金鑫,吴澎.高桩码头抗震性能的pushover分析[J].水利水运工程学报,2010(4):1-8.(LI Ying,GONG Jinxin,WU Peng.Research on pushover analysis method for seismic performance of pile-supported wharf structure[J].Hydro-Science and Engineering,2010(4):1-8.(in Chinese))

