光纤环的每层匝数不同对光纤陀螺温度性能影响

冯文帅，王学锋，王 巍

（北京航天时代光电科技有限公司，北京 100854）

光纤陀螺是一种基于Sagnac效应的新型全固态仪表，具有可靠性高、寿命长、启动速度快、动态范围大等优点[1]。光纤环作为光纤陀螺的敏感部件，其性能直接影响了光纤陀螺的精度。当沿着光纤存在随时间变化的温度梯度时，光纤陀螺会产生热致非互易性相移，即 Shupe误差[2]，若不采取有效的措施，Shupe误差将会累加，并给陀螺带来大的漂移从而限制其应用。

四极对称绕法很大程度上抑制了温度梯度效应的影响，与普通柱形绕法相比，抑制因子约为光纤环层数的平方，因此普遍应用到光纤环的绕制技术上。但是四极对称绕法实际绕制中通常存在最外两层未绕满等每层匝数不同的情况，对光纤陀螺温度性能有一定的影响。国内外对光纤环温度方面的研究大多以整层为单位进行研究，对于光纤环的每层匝数不同这种情况没有分析[3]。

研究光纤环的每层匝数不同对陀螺性能的影响，必须进行合理的光纤环温度分布建模。Mohr模型[3]是常用的光纤环温度建模方法，以电路传输线的电流流动原理为基础来分析热传导过程。但 Mohr模型在长时间(超过半小时)的热传导过程中出现较大的偏差，与实际情况不符。

本文提出以匝为单位对光纤环的每层匝数不同进行研究，并基于已知边界温度条件的插值型温度分布模型，理论与试验研究了光纤环的每层匝数不同对陀螺温度性能的影响。

1 四极对称绕制光纤环Shupe误差理论分析

1.1 四极对称绕制光纤环Shupe误差模型的量化分析

根据文献[4-5]，如图1所示，整个光纤环累积的Shupe误差为：

图1 光纤环上的温度扰动引起的Shupe误差Fig.1 Shupe bias errors resulted from temperature fluctuations in fiber coil

式中，λ为光纤环中传播的光波长，c为光在真空中的传播速度，dndT为石英光纤折射率的温度系数，Δ˙(z,t)为沿光纤的温度分布变化率，L为光纤总长度，z为dz段光纤距光纤起始端的长度。

为了便于计算光纤陀螺的Shupe误差，需要根据四极对称绕制光纤环的结构将式(1)进行量化分析。在文献[5]中，分析光纤环累积的Shupe误差时，以整层光纤为单位进行分析，即每层光纤环匝数相同，且均绕满，如图 2(a)所示。但实际光纤绕制中，为了保证光纤稳定且固定，上层光纤均落在光纤之间或者光纤与骨架形成的凹槽上，因此每层光纤的匝数是不同的，如图2(b)所示，这样的情况下以整层光纤来分析存在一定的偏差。

同样，由于光纤陀螺的指标要求(零偏稳定性、标度因数)限制，同一型号光纤陀螺中光纤环的长度通常已提前确定，然而在光纤环绕制过程中，由于骨架尺寸的限制或者光纤的直径大小不均匀，会导致光纤环绕制完成时最外两层光纤不能实现完全绕满，如图2(c)所示。对于这种情况下光纤陀螺的Shupe误差，必须采用以匝或者更小的单位进行研究。

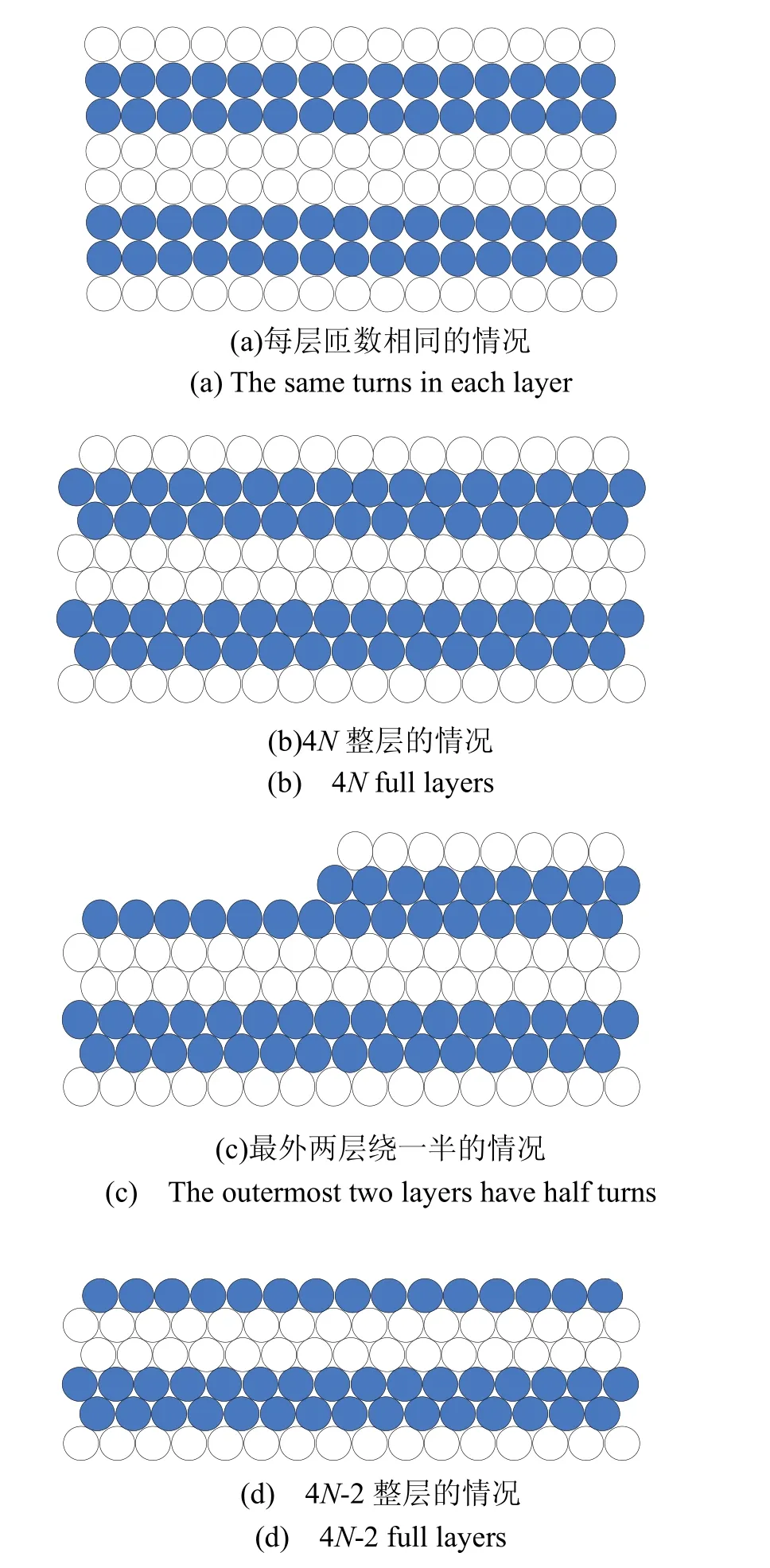
图2 无骨架光纤环每层匝数不同示意图Fig.2 Turns’ difference in each layer of non-framework fiber coil

本文以匝为单位，对光纤陀螺的Shupe误差进行量化分析，式（1）可以变化为：

式中，N为光纤环的总匝数，Li_s是第i匝光纤起始端距光纤环起点的距离，Li_e是第i匝光纤结束端距光纤环起点的距离。

假设光纤环沿径向以及轴向温度变化均匀，即同一匝光纤的温度变化率ΔT（˙z,t）相同，则式(2)可转化为：

根据Sagnac光纤干涉仪用于测量旋转角速率时，相位差ΔΦ与光纤环总长度L、线圈平均直径D、和旋转速率Ω的关系，可以得到以匝为单位的光纤陀螺热致速率误差为：

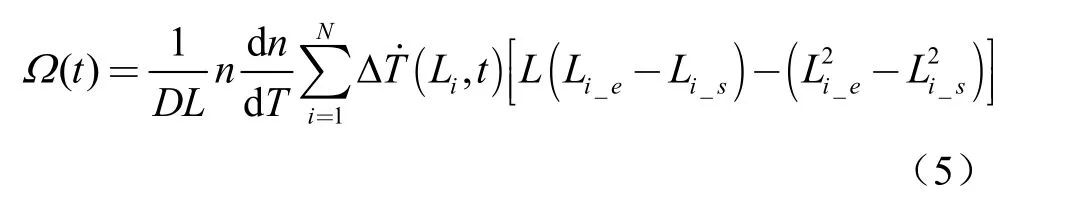
为了研究光纤环的每层匝数不同对光纤陀螺温度性能的影响（本文主要分析的是光纤环最外两层匝数与其他层匝数不同的情况），取了三种最外两层匝数不同的情况，分别为理想的4N满层情况、4N层中最外两层绕制一半的情况、4N-2满层的情况(N为整数)，如图 2(b)、(c)、(d)所示。

根据式(5)，理想的4N满层光纤环的陀螺热致速率误差为：

式中，Q、Q-1分别为四极对称绕法每相邻两层的匝数，（˙m,p,t）为光纤环第m层中第p匝光纤在t时刻的温度变化率，L（m,p）s为光纤环第m层中第p匝光纤起始端距光纤环起点的距离，L（m,p）e为光纤环第m层中第p匝光纤结束端距光纤环起点的距离。

光纤环4N层中最外两层绕制一半的情况与4N-2满层的情况的陀螺热致速率误差均可以通过式(5)得出。

1.2 光纤环的温度分布模型

本文建模分析所选的参数及其意义如表1所示，为了便于与实验结果相比较，各参数取值与下面将要提到的实验光纤环保持一致。

陀螺的电路部分以及散热部件作为热源，以近似恒定的功率向光纤环散发热量。本文主要分析热源施加于光纤环径向时，其温度梯度对陀螺温度性能的影响。Mohr模型用在光纤环温度建模时，在长时间的热传导过程中温度值会出现较大的偏差，如图3所示，在恒功率加热源持续施加在光纤环外壁的情况下，光纤环外壁（图右侧）温度急剧上升，然后趋于平稳，但是在超过半个小时后温度出现下降，并且低于光纤环内壁（图左侧）的温度，这与实际情况不符，因此需采用更合理的温度模型。

本文根据实际测量的光纤环内外壁温度值，来建

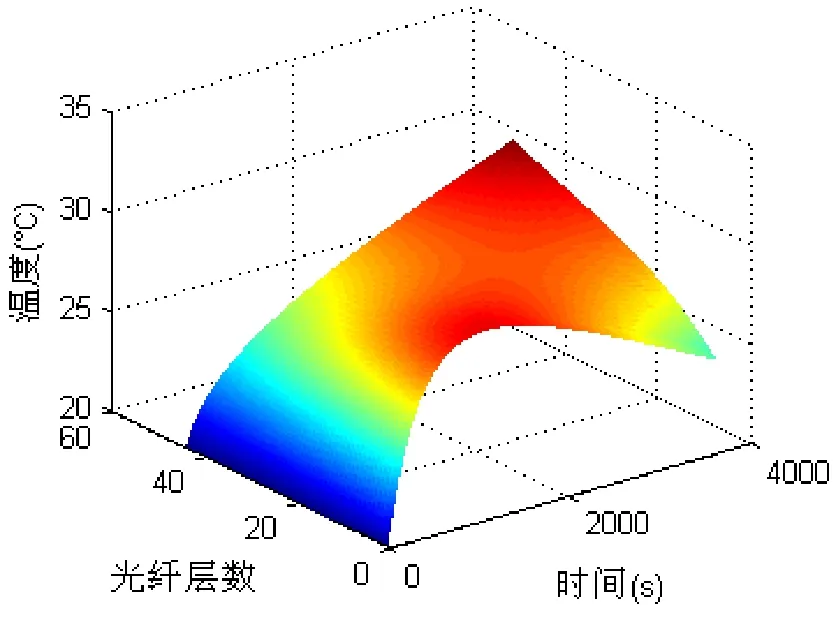
图3 基于Mohr模型的光纤环温度分布Fig.3 Temperature distribution of fiber coil based on Mohr model

式中，x为光纤环内某一匝光纤距环内壁的距离，rn为光纤环内壁的半径，d为环径向上的宽度。

光纤环的温度激励采用如下方式，首先在常温下保持1 h，然后开启恒功率加热源，保持2 h，最后关闭恒功率加热源，保持2 h后结束。根据实际测量的光纤环内外壁温度，代入式（7），得到插值型的光纤环温度分布，如图4所示。

根据每匝光纤所在光纤环内部的位置，可以得到每一匝光纤的温度变化率，代入式（6），可求得光纤陀螺的热致速率误差。

图4 基于已知边界温度条件的插值型光纤环温度分布模型Fig.4 Interpolation temperature distribution of fiber coil based on known boundary temperature

表1 光纤环温度模型的参数取值Tab.1 Parameters on temperature distribution model of fiber coil

2 光纤环的每层匝数不同对陀螺温度性能影响的理论研究

2.1 热源在外的径向温度梯度的影响

外部环境温度的变化通常会导致光纤环存在由外至内的温度梯度。本文选用恒定功率(3 W)的由外至内的温度激励下光纤环的径向温度边界信息，温度激励方式为上一节中的恒温→升温→降温的变温方式，图5(a)为光纤环内外壁的温度变化曲线，图5(b)为不同最外两层匝数的光纤环受图 5(a)的温度场下陀螺速率误差仿真曲线。为了减小噪声的影响，对陀螺仿真输出进行平均时间为100 s的平滑处理，横轴采用100 s为单位。图中可以看到，在施加与关闭加热源的瞬时（温度变化率达到4 ℃/min），陀螺产生较大的热致速率误差，并随着温度变化率的减小与光纤环径向温度梯度的逐渐一致，陀螺输出误差趋于零。

图5 由外至内的径向温度激励下光纤环的每层匝数不同对陀螺速率误差的影响Fig.5 Influence of turns’ difference in each layer on rate errors of FOG with inward radial temperature gradient

对比三种最外两层匝数不同的光纤环情况，可以看出，在开启与关闭温度激励的瞬时，4N层光纤环与4N-2层光纤环的陀螺速率误差符号方向相反，这是由于它们最外两层光纤的次序不同，如图 2(b)与图 2(d)所示，4N-2层光纤的最外两层未组成一个四极，但由于不破坏光纤环关于中点的温度对称性，故其陀螺速率误差与4N层光纤环的陀螺误差峰值相比近似相同。

特别注意的是，对于最外两层绕制一半的光纤环，由于其介于4N层与4N-2层中间，其陀螺速率误差在一定程度上抵消了一部分，并且同样由于未破坏光纤环关于中点的温度对称性，因此其输出误差非常小，仅为4N层与4N-2层光纤环的40%。

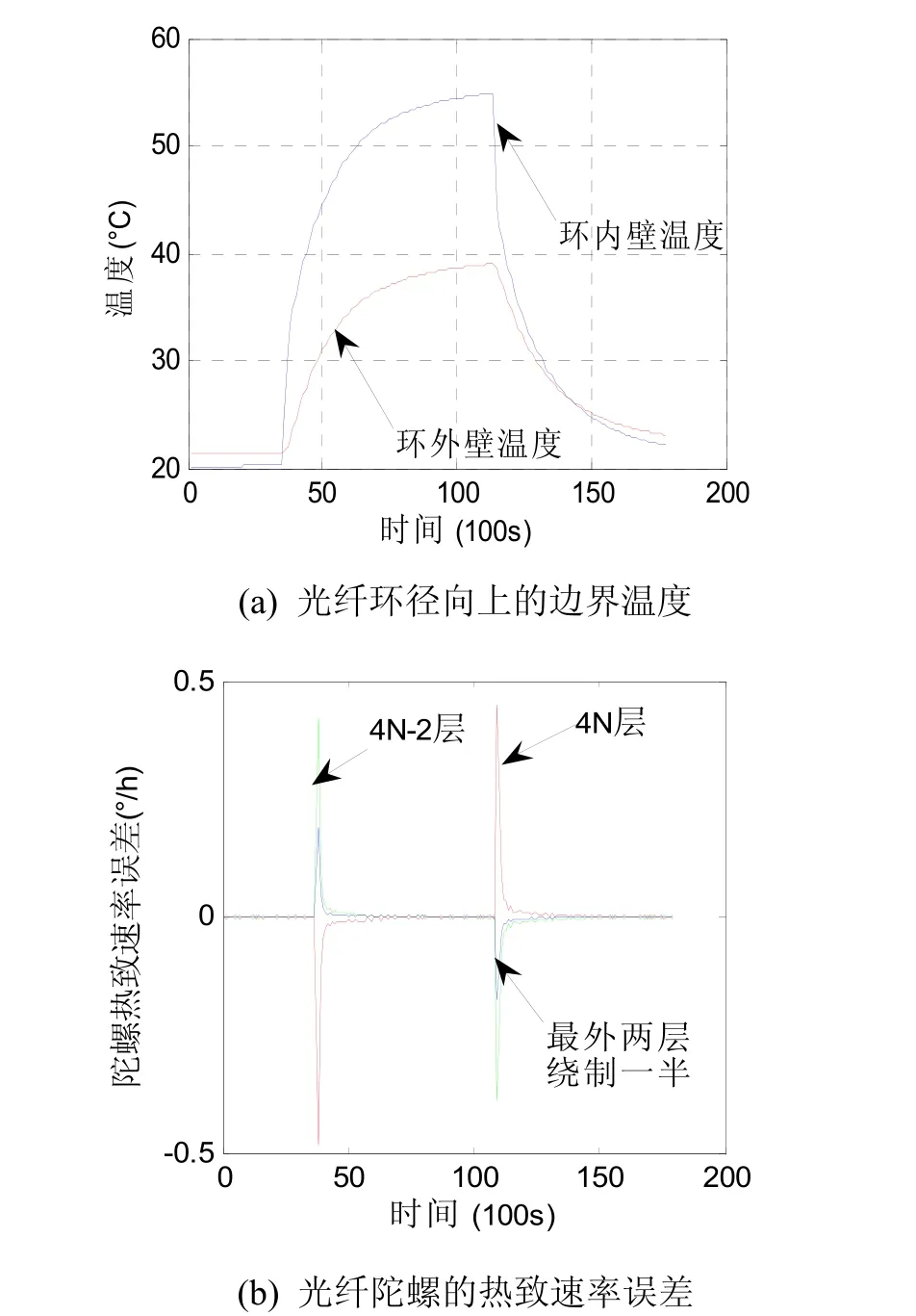
图6 热源在内的径向温度激励下光纤环的每层匝数不同对陀螺速率误差的影响Fig.6 Influence of turns’ difference in each layer on the rate errors of FOG with outward radial temperature gradient

2.2 热源在内的径向温度梯度的影响

光纤陀螺的部分散热器件在光纤环的内部，如SLD光源等，其对光纤环产生的温度梯度是由内至外的。本文选用恒定功率(3 W)的由内至外的温度激励下光纤环的径向温度边界信息，图6(a)为光纤环内外壁的温度变化曲线，图6(b)为不同最外两层匝数的光纤环受图6(a)的温度场下陀螺速率误差仿真曲线。同样，从图6(b)可以看出，最外两层绕制一半的光纤环相对于 4N层、4N-2层的光纤环，其陀螺速率误差更小，约为其他两种绕满情况的 40%，更好地抑制径向温度梯度对陀螺的影响。

3 光纤环的每层匝数不同对陀螺温度性能影响的试验研究

3.1 试验设计

为了检验光纤环的每层匝数不同（本文主要分析最外两层匝数不同）对光纤陀螺温度性能的影响，设计并组成了一套光纤环的最外两层匝数不同对陀螺输出影响的检测装置，示意图如图7所示。光纤环置于相应的温度激励与温度传感装置中，如图8所示。该装置包括上下盖、内外环、温度传感器、薄膜加热片、无骨架光纤环与导纤管等。由于采取径向温度激励，需要做到轴向上隔热，所以上下盖需选用隔热性能好的材料来制作。径向温度激励由薄膜加热片来实现，本试验增加了薄的金属环，将薄膜加热片通过导热双面胶紧贴在金属环上，同样金属环还可以起到支撑上下盖，固定温度传感器的作用。

为了测试径向温度梯度下光纤环内外壁的温度，在光纤环内外壁分别设置了2个Pt1000温度传感器，具体位置如图8所示。

图7 光纤环的每层匝数不同对陀螺温度性能影响的检测系统Fig.7 Measurement system that detects the influences of turns’difference in each layer on temperature performance of FOG

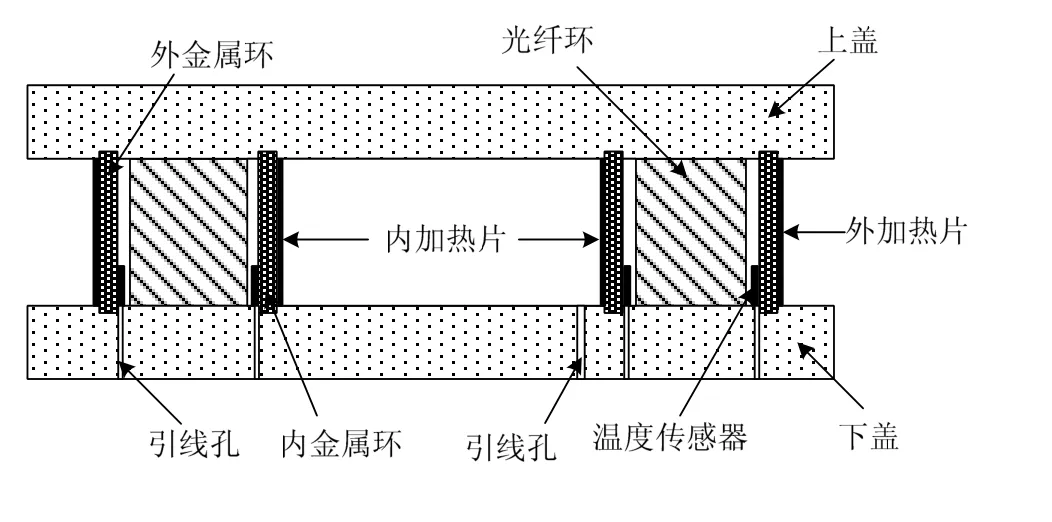
图8 无骨架光纤环的径向温度激励与温度传感装置示意图Fig.8 Diagrammatic sketch illustrating the radial temperature gradient generator and the temperature sensor device

最后通过陀螺测试电路以及采温电路板将陀螺数据和温度信息转换并发送至计算机。

为了分析光纤环的最外两层匝数不同对光纤陀螺温度性能的影响，需要将最外两层匝数不同的光纤环熔入光纤陀螺系统中，然后对陀螺的输出进行比较。本文对最外两层匝数不同的光纤环的实现有如下步骤：

首先选择符合试验精度要求的4N满层的光纤环，如图2(b)所示；

将4N满层的光纤环的最外两层各拆下一半，形成最外两层绕制一半的光纤环，如图2(c)所示；

将最外两层其余的光纤全部拆下，形成4N-2满层的光纤环，如图2(d)所示。

将上述三种光纤环分别熔于检测系统中，施加相同的温度激励，得到相应的陀螺输出数据。

3.2 实验结果与分析

由于陀螺噪声较大，试验分析时将陀螺输出数据进行平均时间为100 s的平滑处理。由于陀螺未做相应的磁屏蔽，以及对于三种光纤环情况下的试验陀螺光路的状态存在差异，因此对于不同次的试验，陀螺输出的零位并不相同。但是从第2节中的理论研究可以看到，陀螺对环境温度的变化响应为输出的漂移，与陀螺零位无关。

图9为光纤环最外两层匝数不同的情况下在由外至内的径向温度梯度下陀螺输出的差异，图中可以看出，在开启与关闭温度激励源的瞬时，三种类型光纤环均产生一个较大的热致速率误差峰值，随着温度变化的减缓，陀螺的漂移逐渐减小，并淹没在陀螺噪声中。对比图9各子图可以发现，在开启与关闭温度激励源时，均为最外两层绕制一半的光纤环的陀螺速率误差最小，约为其他两种绕满情况的1/3，抑制同样的温度梯度带来的漂移程度最佳。

图10为不同最外两层匝数的光纤环受由内至外的径向温度激励下陀螺的输出曲线。图中可以看出，在施加与关闭温度激励的瞬间，三种光纤环类型的陀螺同样均会产生一个较大的误差输出，并随着温度变化的减缓和热量的传递，陀螺输出逐渐趋于稳定。对比图10各子图可以发现，与热源在外的情况相同，光纤环最外两层绕制一半的陀螺受温度梯度影响的输出误差最小，约为其他两种绕满情况的1/2。

通过对光纤环最外两层匝数不同的陀螺进行试验，试验结果显示，光纤环最外两层绕制一半的陀螺温度性能优于其他两种绕满的情况，与第 2节理论研究相一致。但是光纤环最外两层绕制一半的情况光纤陀螺受温度激励影响下产生的漂移仍较大，与理论研究中抑制温漂的程度不同。分析试验曲线与理论曲线的差异有以下原因造成：

图9 热源在外时光纤环最外两层匝数不同对陀螺输出的影响Fig.9 Graphical depiction illustrating the influence of turns’ difference in outmost two layers on the FOG output with inward temperature gradient

图10 热源在内时光纤环最外两层匝数不同对陀螺输出的影响Fig.10 Graphical depiction illustrating the influence of turns’ difference in outmost two layers on the FOG output with outward temperature gradient

1）光纤环的最外两层经过拆取之后，其最外层的温度与拆取前最外层的温度不相同，导致实际热场分布比理论研究的复杂；

2）光纤环沿径向传热不均匀，导致实际光纤环内部温度分布与理论研究的不一致；

3）除了受光纤环最外两层的匝数影响外，陀螺输出还与光纤环的热应力、偏振交叉耦合等有关。

4 结 论

本文对光纤陀螺的Shupe误差建立了以匝为单位的量化分析模型，可分析多种绕制状态以及光纤环的每层匝数不同对光纤陀螺温度性能的影响。建立了基于已知边界温度条件的插值型光纤环温度分布模型，定量分析了光纤环径向温度激励造成陀螺的热致速率误差。试验验证了光纤环最外两层绕制一半时陀螺热致速率误差减小了50%以上，与仿真结果基本一致，验证了以匝为单位光纤陀螺Shupe误差模型的合理性，并可应用于检验光纤环性能的优劣。

（References）：

[1] Lefevre H C, Bergh R A, Shaw H J. All-fiber gyroscope with inertial navigation short term sensitivity[J]. Optics Letters, 1982(7): 454-456.

[2] Shupe D M. Thermally induced nonreciprocity in the fiber-optic interferometer[J]. Applied Optics, 1980, 19(5):654-655.

[3] Blin S, Kim H K, Digonnet M J F, Kino G S. Reduced thermal sensitivity of a fiber-optic gyroscope using an air-core photonic-bandgap fiber[J]. Journal of Lightwave Technology, 2007, 25(3): 861-865.

[4] Mohr F. Thermooptically induced bias drift in fiber optical Saganc interferometers[J]. Journal of Lightwave Technology, 1996, 14(1): 27-41.

[5] 贾明，晁代宏，张春熹. 光纤陀螺的热分析与热设计方法[J]. 中国惯性技术学报，2008，16(6)：725-729.JIA Ming, CAO Dai-hong, ZHANG Chun-xi. Thermal analysis and design for fiber optic gyroscope[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 725-729.

[6] 杨孟兴，陈俊杰. 光纤陀螺静态温度特性的分析及实验研究[J]. 中国惯性技术学报，2009，18(6)：751-755.YANG Meng-xing, CHEN Jun-jie. Analysis and experiments on static temperature characteristic of FOG[J]. Journal of Chinese Inertial Technology, 2009,18(6): 751-755.