一种基于改进Turbo编码的盘旋无人机测控算法

黄 鹤，王小旭，梁 彦，潘 泉，许 哲

（西北工业大学 信息与控制研究所，西安 710072）

无人机测控技术是指对无人机进行遥控、遥测、跟踪定位和信息传输的技术。这里的遥控是指对无人机飞行状态和设备状态的控制；遥测是指对无人机飞行状态和设备状态参数的测量；跟踪定位是指对无人机实时连续的位置测量；信息传输是指无人机任务载荷传感器信息的传输。测控信道[1-2]特征对数据的可靠传输有着极大的影响, 而无人机在不同飞行状态下又具有不同的信道特性,进而直接影响着数据的可靠传输。根据飞行过程中环境的不同 ,可将无人机飞行过程划分为途中飞行状态、任务区域盘旋状态和起飞/降落状态。无人机通信由于受设备重量和体积限制，其天线孔径较小，飞行过程中，特别是无人机在盘旋时，运动速度和电波传播的夹角是周期性变化的,造成直视分量的入射角和最大多普勒频偏都呈周期性变化，信道条件可能受到干扰而变得十分恶劣，引起接收信号的衰落。因此通过改进编码技术提高微弱信号的接收能力不仅能够改善接收效果，还能够提供减小发射功率，提高无人机定位信息传输的隐蔽性。

仿真与实验表明，Turbo码不仅具有接近香农极限的误码率性能，还具有编码简单、易于实现等特点，目前主流的Turbo译码器已经能够达到100Mbps的处理能力，为Turbo码在航空测控领域的应用奠定了基础。对于使用级联编码的通信系统，传统的RS-Turbo码，RS-RSC码，以及MIMO情况下，Turbo-BLAST级联码或者Turbo-STBC码等[3-7]。在不考虑MIMO增益的情况下，使用RS-Turbo码的系统需要提供RS译码及Turbo译码两种不同的译码算法需求，使得译码器的软硬件设计复杂化，不适合工作状态的无人机测控。针对以上情况，本文设计了一种改进的Turbo编码方法，并应用在盘旋状态的无人机测控过程中，并通过仿真分析改进算法的BER性能。

1 改进的Turbo编码器模型

本文设计改进的二维编码码块结构如图1所示，对于信息位不再以比特流的形式出现，而是以矩阵方式出现，首先对信息以行为单位进行行编码，得到行校验位，然后以列为单位，对整个码块进行列编码，得到列校验位以及行校验比特的校验比特。为了简化说明，我们假设信息比特流矩阵的行与列数相等。

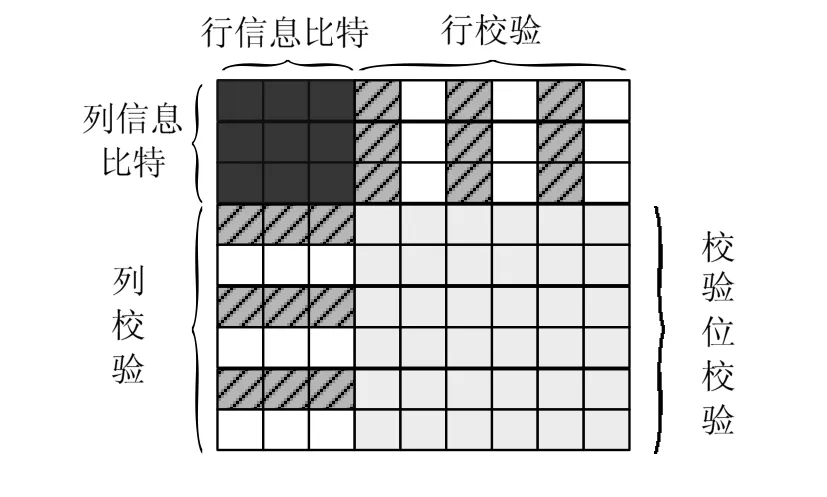
图1 二维turbo编码码块结构Fig. 1 Structure of 2 D Turbo code block

由图1可以看出，假设使用的一维Turbo编码器的编码速率为R，则最后产生的二维Turbo码的编码速率为R'=R×R。图2为在文中设计的使用“软输入软输出”类的MAP译码器，对Turbo码进行译码时，首先使用的外信息(Extrinsic Probability)初始化为，表示每个比特在初始时为0或者1是等概的，经过一次迭代后，由第一次迭代后的后验条件概率信息：

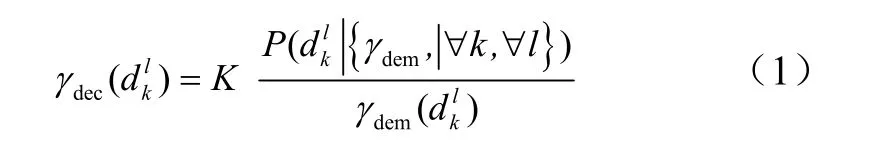
针对译码器的新的先验信息进行下一次迭代，其中，k为第k个调制符号，l为调制符号中的第l个比特，K为比例因子。而对于二维Turbo码译码，首先对码块矩阵各列进行Turbo迭代，之后再将各列的后验条件概率信息作为行Turbo迭代译码的先验概率进行矩阵各行的Turbo译码迭代。由于在行译码之前的先验信息的概率不相等，可知在经过较少迭代次数之后即可达到边际值。即在经过二维编码之后，理论上可以降低译码迭代次数，提高二维编码结构的吞吐率。

图2 二维turbo码译码器Fig.2 2D Turbo code decoder

2 系统模型及仿真

2.1 无人机测控信道模型

由于航空信道模型与一般的移动信道模型不尽相同，参考文献[1]给出了一种实用的无人机通信信道统计模型的生成方法以及参数设置。基于统计模型研究无人机测控信道特性可以发现，与陆地移动通信系统不同，前者存在较强的直视信号(LOS)分量和一定的高斯白噪声分量。

设在各个子信道上对应的信噪比为r= [r1,r2,r3...rn]，其中ri表示第i个信道上对应的信噪比。则各个子带对应的整个宽带信噪比为：

2.2 基于改进Turbo编码无人机测控系统

由于无人机测控信道业务量相对较小，通常12.8 kbps即能满足要求，如果采用改进的二维Turbo码对测控信道数据进行编码，则需约164 kbps信息速率，假设无人机子信道为64 kbps，则需大约3个子信道即可满足要求，对带宽要求增加不大。而任务信道由于需要传输的图像、传感器等信息所需的任务数据一般较大，从24 kbps到6 Mbps不等。如果采用上限6 Mbps，经过二维编码后的带宽需增加 30M 左右，考虑到目前无人机通信带宽的限制大约在 20M，二维Turbo编码目前更适用于测控信道。而由于Turbo译码器目前的处理速度已经达到100 Mbps，在带宽允许的情况下，二维Turbo码也能够应用于任务信道中。

在测控信道中，UAV系统对由基站发送信息进行接收，经信道估计后，对信道进行辨识。假设基站对UAV下行信道包含2K个导频符号S。信道上的有用功率为：

在完成信道估计后，接下来需要进行解调制，使用解调制后的软信息送入 Turbo译码器中进行 Turbo译码，最终得到信息比特。

2.3 系统仿真与性能分析

理想AWGN信道时改进的二维Turbo编码的通信系统与传统Turbo编码系统的BER性能曲线的对比如图3所示。

图3 二维Turbo码与一维Turbo码性能比较Fig.3 Turbo code & 2D Turbo code performance comparison

从图3中可以看出，对于二维Turbo编码系统，在进入0 dB以上传统意义上的“低信噪比”区域时，其BER性能很快既能到达10-4量级，相比较传统的一维Turbo码，其性能有大约2～3个dB的提升。由图3中还可以看到，对于2维Turbo编码，可以在保证译码BER到达错误平层时大大减少译码迭代的次数，由大量仿真实验的结果可以得到一般迭代次数为2即可保证译码准确性。通过聚类分析，在大于0 dB处具有误比特率对平均信噪比变化的拐点，得到信噪比分布与最优迭代次数关系如表1所示。由表1中我们可以看出，二维Turbo码最大译码迭代次数仅为4次，相比较一维Turbo码的通常迭代次数8次而言减小了至少一半。

对采用改进算法的无人机测控信道进行仿真，仿真条件为：采用64k带宽的子信道和16QAM调制，信息速率为256 kbps，Turbo编码采用码率为1/3的约束长度为 3，生成多项式为(5,7)8的 RSC码进行二维Turbo编码，交织器采用长度为128的伪随机交织器。取无人机信道模型为小尺度衰落信道 WSSUS模型（Wide-Sense Stationary Uncorrelated Scattering，广义静态非相关散射），并在起/降、盘旋、途中飞行三种状态下分析系统性能。UAV速度设置为 50 m/s。其BER性能曲线如图4所示，从图中可以看出，随着飞行状态的不同在Los分量的提高的情况下，无人迹的系统性能也随之提高。

图4 盘旋UAV典型信道状况下2-D Turbo码性能Fig. 4 Performance of 2D turbo code in typical UAV channel

表1 信噪比与最优迭代次数关系表Tab.1 Relationship between SNR and optimal iteration times

由于二维Turbo编码的编码效率相对传统的Turbo码有所降低，因此考虑在高SNR时将二维Turbo码进行删余处理。图 5所示为删余后二维 Turbo码在AWGN信道的性能，可以看出，将二维Turbo码中“校验位的校验”删余后其性能有所退化，此时其码率为1/5，当将二维Turbo码的行校验和列校验位也进行删余使得码率等于传统Turbo码速率的1/3时，其性能也退化至与传统Turbo相当的水平。

表2 反馈编码方案及运算量Tab.2 Feedback encoding scheme and calculation

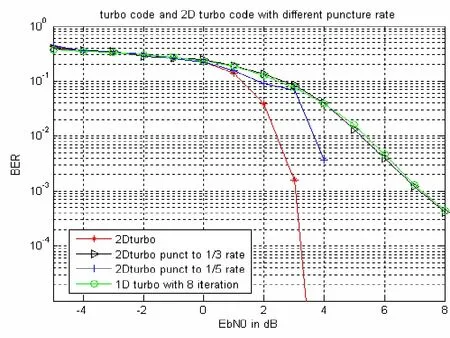
图5 删余二维turbo码与一维turbo码性能比较Fig.5 Punctured 2D turbo code and turbo code performance comparison

根据10-4误差限，定义一个最优的二维Turbo编码方式及迭代次数关系，如图2所示。由于在0 dB信噪比以下二维Turbo码性能提升很少，可以提高编码效率牺牲性能；在0～8 dB时可以使用二维Turbo码提升系统性能；在信噪比高于8 dB时可以采用1/3码率的删余Turbo码以提升系统效率。

3 结 论

本文提出了一种基于改进Turbo编码的盘旋无人机测控算法，对其在典型无人机测控信道及不同迭代次数情况下的性能进行了仿真。改进Turbo编码与传统一维Turbo编码系统性能相比，该算法不增加系统译码算法设计的复杂度，仅仅只需要在编码上进行的改动，具有很大的灵活性，同时可以在更低的SNR时获得较好的BER性能，具有更好的纠错能力，并能够在较少的译码迭代次数时就到达错误平层，非常有利于无人机定位信息传输。仿真结果表明，该算法可以实现的盘旋状态下的无人机测控

[1] 金石，张晓林 无人机通信信道的统计模型[J]. 航空学报，2004，25(1)：62-65.JIN Shi, ZHANG Xiao-lin. A statistical model for the UAV communication channel[J]. Aeronautic Astronautica Sinica, 2004, 25(1): 62-65.

[2] 王波，叶晓慧. 无人机飞行状态对数据传输的影响研究]

[J]. 舰船电子工程，2008，28(10)：40-43.WANG Bo, YE Xiao-hui. Research on the influence of UAV flight state on data transmission[J]. Ship Electronic Engineering, 2008, 28(10): 40-43.

[3] Eun Cheo Kim, Jin Young Kim. Double binary turbo coding for BPPM-TH and BPAM-DS UWB systems[C]// IEEE International Conference on High Performance Computing and Communications, 2009: 444-449.

[4] 何业军，朱光喜，刘文明. 基于turbo乘积码的MIMO-OFDM系统在IMT2000信道下的性能仿真[J].通信学报，2005，26(8)：107-111.HE Ye-jun, ZHU Guang-xi, LIU Wen-ming.Performance of MIMO-OFDM system based on Turbo product codes over IMT2000 channels[J]. Journal of Communications, 2005, 26(8): 107-111.

[5] Lin Yi-nan, Hung Wei-wen, Lin Wei-chen, et ac. An efficient soft-input scaling scheme for Turbo decoding[C]// IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing. 2006,Vol.2: 252-255.

[6] Sun Yang, Zhu Yuming, Goel M. Application-specific systems[C]// International Conference on Architectures and Processors. 2008: 209-214.

[7] Nissila M, Pasupathy S. Soft-input soft-output equalizers for Turbo receivers: A statistical physics perspective[J].IEEE Transactions on Communications, 2007, 55(7):1300-1307.