小舜江泵站3号泵停机过程振动原因分析

陈喜阳，彭玉成，张克危，竺维佳，施准备

（1.华中科技大学能源与动力工程学院，湖北 武汉 430074；2.浙江绍兴市上虞市汤浦水库有限公司，浙江 绍兴 312000）

0 引言

小舜江泵站位于浙江省上虞市汤浦镇，承担着供水的重任。自泵站建成后，3号和4号机组就存在振动过大的问题。关机过程中，振动尤其剧烈，造成厂房振动超标，成为泵站建筑物的严重安全隐患。为消除这一隐患，泵站方曾与有关单位合作，采取了一些整改措施，包括增加承重地板和横梁加固，开、停机过渡过程仿真计算及阀门关闭过程的优化等，使问题在一定程度上得到了缓解，但始终没有根本解决。作为项目组对3号泵机组停机过程中异常振动机理分析课题研究的部分成果，本文结合现场试验数据，分析其振动原因，为实施降振措施提供依据。

1 现场试验

为获得分析振动原因所必须的数据，项目组于2010年7月8日对3号机组进行了针对性的现场测试 （见图 1）。

图1显示，停机过程中，T4时刻开始，横梁的振动突然大幅增加，最大幅值超过了2 mm。从T3到T4的时间间隔为13.7 s的时段内，阀前和阀后的水压都比较平稳，阀前水压静态值略有增加，但脉动幅度增加比较明显。这显示叶轮内的流态处于最混乱的状态[1]。通常，频率信息是判断振源的主要依据，但由于停机过程中不存在稳定的频率组成，所以不能简单地给出频率组成，需要采用一定的策略进行分析[2]。横梁垂直方向发生强烈振动，极有可能是某种激励的频率与横梁固有频率接近，使其产生共振所致。下文将分析究竟是什么因素导致横梁发生强烈振动。

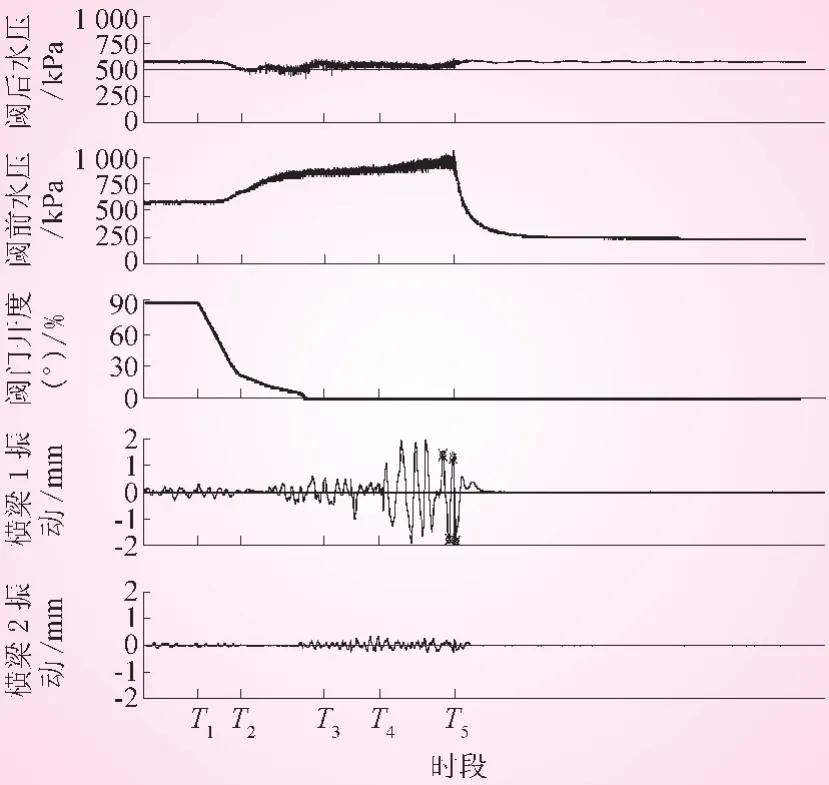
图1 停机过程中几个重要参数的变化过程

1.1 横梁的固有频率测量

剧烈振动现象通常与共振有关，判断是否发生共振，需要知道固有频率，所以需要测量梁的固有频率。由于现场条件的限制，只能采用比较简单的方法——锤击法。此法是用锤击引发梁的自由振动，自由振动就是某一阶固有频率的振动或者若干阶固有频率振动的叠加。

需要说明的是，这里所说的横梁的固有频率，是整个厂房的某一阶振型的固有频率 （因为横梁与整个厂房是一个整体）。由于横梁尺寸较大而锤子质量较小，所激发的振动的幅值很小 （小于0.2 mm），且横梁振动的阻尼较大，每一次锤击只能得到1～1.5个完整的波形，所以不便于进行精确的频率分析。

图2 锤击横梁产生的振动波形示意

图2是锤击横梁产生的振动波形。由图2可见，振动表现出明显的非线性特征，其频率不是恒定的，在一个周期中 （例如从第一个波峰到第二个波峰），两个半周期 （从第一个波峰到波谷为第一个半周期，从波谷到第二个波峰为第二个半周期）的长度并不相等。所以，梁并不具有恒定的固有频率，其频率与振幅相关。

对于这样的振动系统，不便于用传统的傅立叶分析计算其频率，这里采用如下方法进行分析。图2所示为5次锤击产生的振动。其中，第二次和第三次锤击是连续进行的，第二次的振动尚未结束，第三次锤击即已开始。所以第二次所产生的波形是不完整的，不对其进行分析。对其余的取一个完整的波形，将波峰和波谷出现的时刻标记出来并予记录 （以采样点的序号表示），然后计算每半个周期的时间，从而推导出振动频率值 （见表1）。

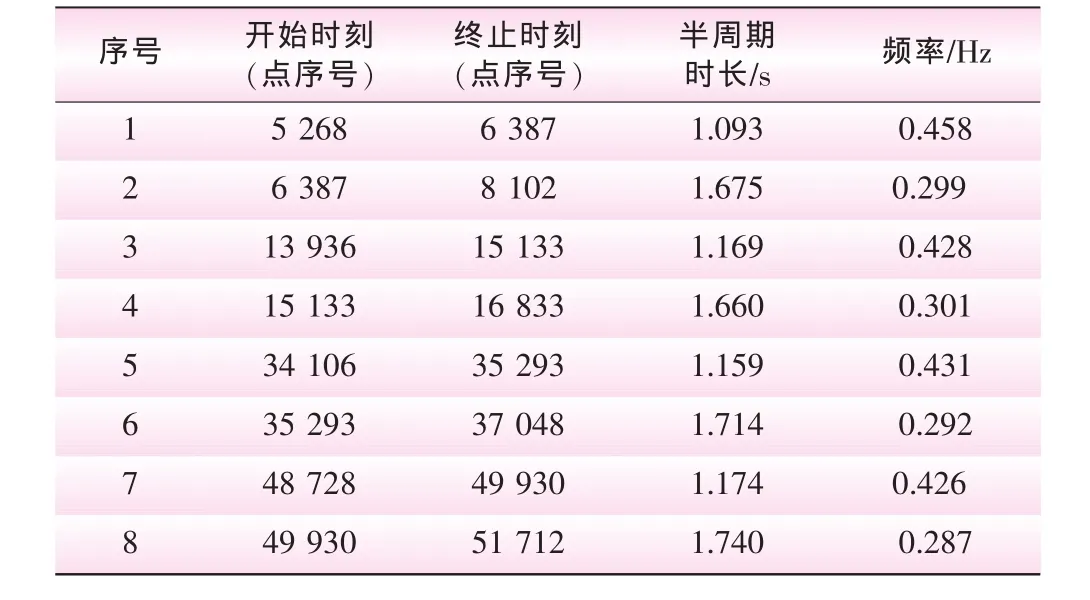
表1 梁的固有频率计算结果

计算结果表明，按前半个周期计算所得固有频率的值为0.428～0.458 Hz，按后半个周期计算所得固有频率的值为0.287～0.301 Hz。各次计算结果的大小与图中各波形的幅值的关系基本是确定的。即，振幅越大，频率越高。综合各次计算结果可知，梁的固有频率为0.287～0.458 Hz，与振幅有关。在泵关机的过程中产生的振动的振幅很大，因此梁的固有频率更高。估计应该达到0.5～0.6 Hz，甚至更高 （停机时振幅达2 mm，而锤击的振幅最大只有 0.17 mm）。

1.2 关机过程中横梁的振动频率

图3给出了关机过程中横梁振动的波形。由图3可见，振动并不是单纯的简谐振动，仍然带有一定的随机成分，频率也不稳定。取停泵前相对比较规则的两个周期进行分析。图3中用⊗表示分析的特征点，两个点是波峰，两个是波谷。两个波峰之间为一个周期，两个波谷之间也是一个周期。按前述方法计算周期的长度和对应的频率，结果见表2。

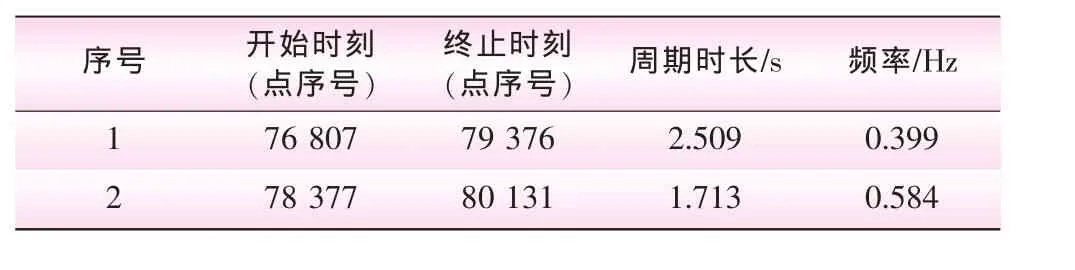
表2 关机过程梁的振动频率

图3 关机过程中横梁1的振动波形

可见，梁的振动频率大约为0.4～0.6 Hz，与前面估计的固有频率相当接近。

1.3 关机过程中阀前水压脉动的频率

根据振动频率分析，横梁剧烈振动的激振力应该是水压脉动的结果，故对阀前水压脉动的频率进行分析。

图4是横梁振动剧烈的时段的阀前水压脉动信号的波形图。图4a中是水压的原始信号和静态信号。由于这个时段是阀门关闭的过程中，泵的工况和阀门处的流态处于不断变化的过程中，给频率分析带来极大的困难。

图4 阀前水压信号的处理

阀门关闭过程中，流量逐渐减小，泵扬程逐渐升高，静态水压也逐渐升高。由于这不是一个周期性的过程，如果直接对原始的信号进行FFT（频谱）分析，会带来较大的误差。为消除静压力逐渐变化的影响，需设法将静压信号从原始信号中剔除，只分析动态信号。为此，首先对原始信号进行滑动平均计算 （每1 s计算1个平均值），得到静态压力随时间变化的规律。由于平均计算的时间只有1 s时间，低于1 Hz的低频脉动也会包含在此平均值之中。由于低频信号对于梁的振动是最重要的信号，不应从原始信号中剔除。所以对所得的静态水压与时间的关系曲线进行一次光顺处理 （光顺样条拟合）。这样，所得的水压静态分量与时间的关系，见图4a中曲线。从原始信号中剔除静态分量以后，得到图4b为纯动态水压信号的波形图，频率分析是针对这样的数据进行的。

剔除静态信号以后，分析仍然面临着一个很大的困难。如果取一个较短的时间段进行分析，那么根据FFT分析的数学原理，不可能得到低频分量的信息。如过取较长的时段进行分析，由于流态是逐渐变化的，所得结果实际上只是这一较长时段里不同状态的某种意义上的平均值，并不是实际的情况。

所以，这里取各种不同时段进行分析 （见表3）。实际上，引起横梁剧烈振动的频率，不是幅值最大的频率分量 （称为主频），而是频率与固有频率最接近的频率分量。所以，表3中除了按照FFT分析的一般做法那样给出主频及次频、季频等分量的幅值以外，还特地给出了可以得到的1 Hz以下的低频分量的幅值。

为使水压分析的时段与横梁分析的时段尽可能一致，分析时段都是从图4的最后时刻向前推算的。

从以上结果可知，虽然以上频率分析的结果不是精确的结果 （原因已如前述），但有一点是明显的，那就是在梁的固有频率范围内 （0.4～0.6 Hz或更高），的确存在着水压脉动的分量。这些分量的幅值虽然小于主频分量，但相对于其他的频率成分还是比较大的。

2 结论

根据上述分析基本上可以确定：横梁的剧烈振动是在阀门开度很小时，泵和管道内水压脉动的低频成分的频率与横梁的固有频率相近，从而产生共振所致。

［1］ 施准备，竺维佳，彭玉成，陈喜阳.基于CFD数值模拟的水泵机组振动分析［M］.水力发电，2010，36(10):62-64.

［2］ 陈喜阳.水电机组稳定性监测中状态分析方法研究 ［R］.武汉：华中科技大学， 2008.