适用于独立变桨控制方式的风机气动模型和风模型的研究

张 迪，王维庆，王海云，李 强

（1.新疆大学电气工程学院，新疆 乌鲁木齐 830047；2.北京金风科创风电设备有限公司，北京 100176）

0 引言

风机变桨控制分为集体变桨和独立变桨，随着风机的容量，叶轮和塔架的尺寸的增加，如何降低风机载荷的问题日益凸显出来，独立变桨同集体变桨相比的优势在于降低风机载荷同时保证风力发电机的输出额定功率。独立变桨是变桨控制发展的趋势。少数国外先进的风机制造商已经将独立变桨应用于兆瓦级风机上，国内先进的风机制造商也加大了对独立变桨控制技术的研究。

随着风机变桨控制方式从集体变桨过渡到独立变桨，由于在传统的应用于3叶片集体变桨控制策略的风机气动模型中，3只桨叶的桨距角对风机气动转矩的影响是耦合在一起的， 无法利用模型来分析单只叶片的桨距角对单只叶片的拍击力和升力的影响，所以需要回到叶素理论中来研究适用于独立变桨风机气动模型的建立方法，因此需要一种新的建模方式。

1 风机气动模型的建立

1.1 应用于集体变桨的风机气动模型

[1]中的风机风能利用系数Cp的经验计算公式为：

式中，λ为叶尖速比；λi为中间变量；β为桨距角；C1=0.5176， C2=116， C3=0.4， C4=5， C5=21， C6=0.006 8。

风轮吸收的功率表达式为：

式中，ρ为空气密度；R为叶片半径；V为风速。风轮产生的转矩为：

式中，ω为风轮转速。

叶尖速比λ的计算公式：

将式（4）和（5）代入式（3）中得出风机气动转矩 T 的表达式为：

基于式 （1）、（2）、（6） 在 simulink 中搭建模型结构，仿真条件为桨距角β取0°，空气密度为1.29 kg/m3，叶片半径40 m；风轮转速ω从0 r/min变化到35 r/min， 风速从3 m/s到14 m/s。

仿真结果：①风机的输出转矩T变化情况如图1中曲线所示；②根据文献[1]，Cp最大值对应的减速比λopt为 8.1，带入式（5）可以计算出最优转速ωopt和与其对应的最优转矩Topt。用光滑的曲线连接形成图1中虚线。虚线中的低风速下段可以作为低风速下最大功率跟踪的T-ω参考曲线。

图1 桨距角为0°，不同风速下叶轮转矩随转速变化曲线

当风速高于额定风速时，通过变桨电机驱动桨叶增大桨距角，降低了Cp，从而降低风机气动转矩，维持风轮转速额定。图2绘制了风速为12 m/s、桨距角为0°，风速为13 m/s、桨距角为1°，风速14 m/s、桨距角5°转矩同转速变化的对比曲线，可以看出增大桨距角对降低气动转矩的效果是非常明显的。

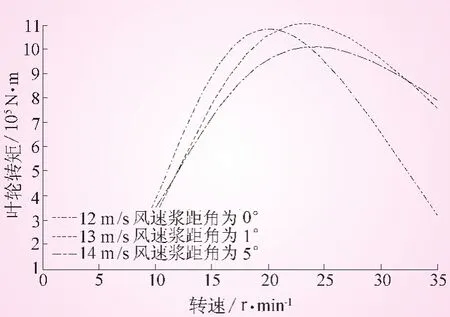
图2 变桨对气动转矩的影响

这种建模的方式可以用于对集体变桨策略的仿真验证，但是对于独立变桨，由于模型没有独立的桨距角输入，而只能输入3个桨叶集体的桨距角，所以无法应用于独立变桨策略的验证。

1.2 应用于独立变桨的风机气动模型

根据文献[2]的叶素理论如图3所示。若以叶素为参考系，风将会叠加一个同叶素转动方向相反，大小相等的线速度-u，风速V和-u矢量合为叶素的相对风速w。w为叶素真正感受到的风速。由于相对风速w的作用，在风机叶素产生了与w同一方向的阻力Fdrag与垂直于阻力的升力Flift。

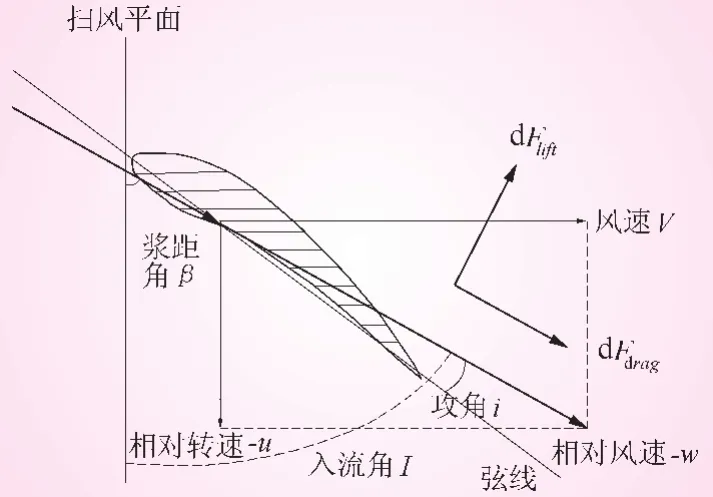
图3 叶素受力分析

式中，Cd为阻力系数，Cl为升力系数，同Cp一样没有量纲，二者的取值变化决定于攻角i，影响Cd、Cl的因素有弯曲度，叶片厚度，表面粗糙度和雷诺数，Cd、Cl数据参考翼型为NACA0015；L为弦长；dr可以理解为一段很短的叶展。攻角变化范围为0-2π。

为了计算出作用在风机主轴上的气动转矩Tair和作用在叶片上的拍击力Fflap，首先需要将叶素上的阻力和推力经行轴向和切向分解与合成 （如图4）。

每一小段叶素上产生的升力dFu和拍击力dFa由公式（10）和公式（11）计算出来

图4 Fdrag和Flift的分解与合成

式中，I为入流角。

为了实现仿真，将微分放大为变化量。将每只桨叶被分为均匀的10段，每段的弦长为此段两端弦长的平均值，分别建立每段叶片的拍击力△Fa和升力△Fu的模型。

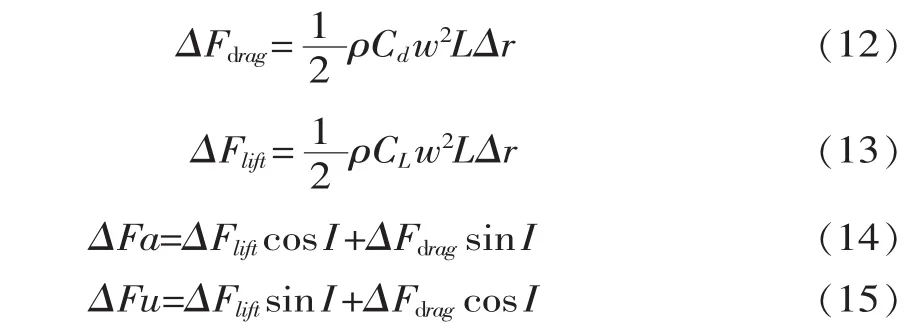
将一只叶片上每段的拍击力△Fai与对轮毂处的转矩△Fuiri求和，最终计算出每只叶片上的拍击力F（flap）j与 3只叶片总体在主轴上的气动转矩 Tair。

式中，i为每段叶片的标号；ri为第i段叶片中心距离轮毂的距离；j为叶片数。

基于式（12）～（17）在 simulink 中建立仿真模型，仿真条件为：空气密度1.25 kg/m3， 叶片长度40 m，风速从3 m/s至13 m/s，风轮转速从0到35 r/min，桨距角保持-1°。

仿真结果如图5，主轴气动转矩随着风速，风轮转速变化曲线。由于桨距角为-1°，所以整体的主轴气动转矩大于图1中的主轴气动转矩。

图5中横坐标为主轴转速，纵坐标为气动转矩，曲线下方的面积为叶轮吸收的风能，根据最大面积的方法同样可以得到最佳转速值以及对应的最佳转矩值作为低风速下的最大功率跟踪T-ω参考曲线。

1.3 两种建模方式的比较

（1）第一种风机气动模型是否可以反映风机的气动转矩关键在于对Cp（λ，β）曲线的拟合准确度，对于不同类型的叶片需要大量的数据进行拟合，而第二种气动模型的建立只需要知道叶片的升力系数Cl和阻力系数Cd，这两个参数可以在对应的叶片参数中找到，能够直接放入模型中，而且由于单只叶片模型由一段段叶片拼接而成，由此就能实现对单独一只叶片的桨距角和风速进行独立修改，可应用于独立变桨中。

（2）第一种风机气动模型无法计算单只叶片的拍击力而第二种模型可以计算。

（3）第二种模型的分段数可以增加，将会更加准确模拟叶片，具有发展潜力。

图5 新模型不同风速下叶轮转矩随转速变化曲线

2 风剪塔影对风机气动模型输出的影响

2.1 风模型同风机气动模型的影响与配合

风剪塔影最终对于风机气动模型模型的影响包括：①在单只叶片上会产生1P的拍击力波动，波动频率为叶轮旋转周期的倒数。②在风机主轴转矩中产生3P的波动，波动频率为1P波动的频率的三倍。塔影引起的波动要比风剪更大。

由于风机的每只叶片被分为10段，风速模型输出的风速也与这10段每一段中心的位置对应。即风速最终都应化为叶片位置角度θ与叶片位置点到轮毂中心距离ri的函数从而风速模型输出30个风速变量与3只叶片中的30个叶片段位置对应。

2.2 风剪切以及与模型配合

风剪切是指当随着高度的不同，风速随之变化从而造成转矩和拍击力的周期性波动，参考文献[3]中的风剪切公式：

式中，V（h）为某一高度处风速；V（h0）为轮毂高度处风速；α为风剪切经验指数，取1/7。

将式（18）转化为每段叶片位置角度的函数如式（19）：

式中，ri为第i段叶片距离轮毂的半径长度；ω为风轮转速；根据式（20）和式（21），作用在单只叶片某段上的风速，会叠加一个频率为 （ω/60）Hz的分量。仿真设定条件为：叶片半径40 m，轮毂高度70 m。转速为19 r/min，桨距角为4°，轮毂处的风速为13 m/s，观察与一段叶片对应的风剪模型的输出风速如图6。

图6 风剪切效应下的风速波动

对风速模型输出的数据经行快速傅里叶变化得到频谱图如图7。

图7 风速频谱图

由图7可以看出，风速中除了直流分量外，还有明显叠加了0.2 Hz谐波含量。

风剪切造成叶片拍击力的1 P波动如图8，频率为0.2 Hz，即等于叶轮旋转周期5 s的倒数，而仿真设定转速为12 r/min，也就是0.2 r/s， 即5 s/r，即叶轮旋转周期周期为5 s仿真结果验证了风剪对单叶片拍击力和气动转矩影响的结论。

图8 风剪切造成叶片拍击力的1P波动

风剪切造成主轴转矩3P波动，频率为0.6Hz如图9。

2.3 塔影效应及与模型配合

塔影效应指塔架正面的风速由于塔架的作用而减小，所以当叶片经过塔架的竖直位置时，叶片上的拍击力会减小，单只叶片旋转一周后由风速引起的拍击力会产生1P波动。而对于3叶片风机，叶轮旋转一周后，每只叶片都经过一次塔架位置，所以在主轴转矩中会产生3P波动。结合文献[3]的塔影效应计算公式得出每段叶片对应位置的风速表达式：

图9 风剪切造成主轴转矩3P波动

式中，a为塔架的半径 ；R为叶片半径；H为塔架高度；x为叶片与塔架的距离；塔影效应只在位置角度θ为π到π内起作用。仿真的其他条件不变考虑塔影效应的情况下观察到单只叶片的拍击中产生了1P波动，主轴转矩中产生3P波动，塔影效应造成叶片拍击力的1P波动，频率为0.2 Hz，如图10。

图10 塔影效应造成叶片拍击力的1P波动

塔影效应造成主轴转矩3P波动，频率为0.6 Hz如图11。

图11 塔影效应造成主轴转矩3P波动

2.4 风剪塔影对风机的影响

风剪塔影都会造成单只叶片的拍击力中的1P波动，主轴转矩中的3P波动，但是由于塔影效应对风速的影响比风剪切更加严重。所以塔影效应产生的波动更加严重。

3 独立变桨对叶片拍击力的影响

为了减小风对叶片拍击力的影响，需要对每只叶片的桨距角进行独立的控制，风速为13 m/s，转速为12 r/min的条件下，3只桨叶的桨距角分别为2°，4°，6°，从仿真结果可以看出桨距角的增大对叶片的拍击力的影响如图12。

图12 独立变桨对叶片拍击力的影响

4 结论

（1）综合比较了基于Cp经验公式与基于叶素理论的风机气动模型，通过分析两种模型构架思想和仿真结果，说明了基于叶素理论的风机气动模型应用于独立变桨的正确性。

（2）在基于叶素理论的风机气动模型与基于风剪切塔影效应理论的风模型基础上，通过分析二者联合仿真的结果，验证了风剪塔影导致单只叶片拍击力的1P波动和3只叶片产生主轴转矩中的3P波动。

参考文献：

［1］ HeierS.GridIntegrationofWindEnergyConversionSystems［M］.1998.

［2］ 叶杭冶.风力发电机组的控制技术［M］.机械工业出版社2002:53-33.

［3］ 李少林，张兴，谢震，等.双馈风力发电系统3次功率脉动的研究［J］.电网技术 2010， 34（4）:38-39.

［4］ Song S H,Jeong B C,Oh J H,et al.Simulation of output characteristics of rotor blades using a hardware-in-loop wind turbine simulator［J］.IEEE Trans on Energy Conversion,2005,3（6）:1791-1796.

［5］ Anderson C G,Richon J-B,Campbell T J.An Aerodynamic Moment-Controlled Surface for Gust Load Alleviation on Wind Turbine Rotors［J］.IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY,1998,6（5）:578-580.

［6］ Dolan D S L,Lehn P W.Simulation model of wind turbine 3p torque oscillations due to wind shear and tower shadow［J］.IEEE Trans on Energy Conversion， 2006， 21（3）:717-724.

［7］ Geyler M,Caselitz P.Individual Blade Pitch Control Design for Load Reduction on Large Wind Turbines［C］//Proceedings of European Wind Energy Conference,2007:1-4.

［8］ 董萍，吴捷，杨金明，等.风力发电机组建模研究现状［J］.太阳能学报 2004， 25（5）:613-615.

［9］ Van Baars G E,Bongers P M M.Flexible wind turbine model validation［J］.Wind Engineering,1992,16（4）:247-256.

［10］ Muljadi E,Butterfield C P.Pitch-Controlled Variable-Speed Wind Turbine Generation［J］.IEEE Trans on Industry Applications,2001,37（1）:240-246.