连续T梁桥面混凝土铺装层力学行为数值分析研究
马文栋
(河北省高速公路管理局,河北 石家庄 050043)
0 引言
随着我国公路交通迅速发展,桥梁的应用也越来越多,桥面铺装层出现了严重的破坏,引起了一些学者的研究。部分学者在桥面铺装层的受力状态分析、破坏机理等方面进行了大量研究,并得到一些有益的结论[1-10]。顾兴宇[11]讨论了振动频率与振型、车辆荷载和结构特点对桥面系的受力影响,得到桥面系的动力系数,并发现静力分析的结果与动力分析的结果在某些方面具有一致性。
目前对桥面铺装层的研究大多集中于铺装层本身的物理力学性能及其受力状态,缺乏有针对性的桥梁整体结构受力性能的研究。本研究以河北省大广高速公路衡大段筹建处所立科研项目为依托,选取滏阳新河特大桥的其中一联为研究对象,通过对其建立三维实体模型进行有限元分析,分析典型混凝土桥梁结构及其桥面铺装层的共同的受力状态、研究不同影响因素对铺装层力学响应的影响,从而指导实体工程,为铺装层的材料选择、设计以及施工控制提供参考依据。
1 建立铺装层受力分析的三维有限元模型
1.1 基本假定
对桥梁混凝土铺装层建立三维实体模型,为了便于运用有限元进行受力分析,现对模型的结构特性和材料特性作以下假定:
(1)在车辆荷载作用下混凝土桥面体系是均匀的、连续的、各向同性的弹性材料,桥梁部件之间的链接均为连续。
(2)根据圣维南原理,远离荷载作用点的支撑条件对荷载作用点附近的受力影响可以忽略不计。本研究采用固结约束施加在两端横梁的底端面上,这种支撑方式相对于其它方式对结构应力分析产生的影响不会很大。
(3)铺装层表面自由,其上分布车辆荷载,且不考虑混凝土桥梁和铺装层的重力作用。
1.2 有限元分析及ABAQUS
有限元是将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。ABAQUS包括一个丰富的、可模拟任意几何形状的单元库,并为用户提供了广泛的功能,能解决大量结构(应力/位移)问题,它不仅能够选择合适参数,而且能连续调节参数以保证在分析过程中有效地得到精确解。
1.3 计算模型及基本参数
(1)单元的选择。在采用ABAQUS进行有限元力学分析中,桥梁采用如图1(a)所示的8节点的六面体等参单元,桥面混凝土铺装层采用壳单元,如图1(b)所示。
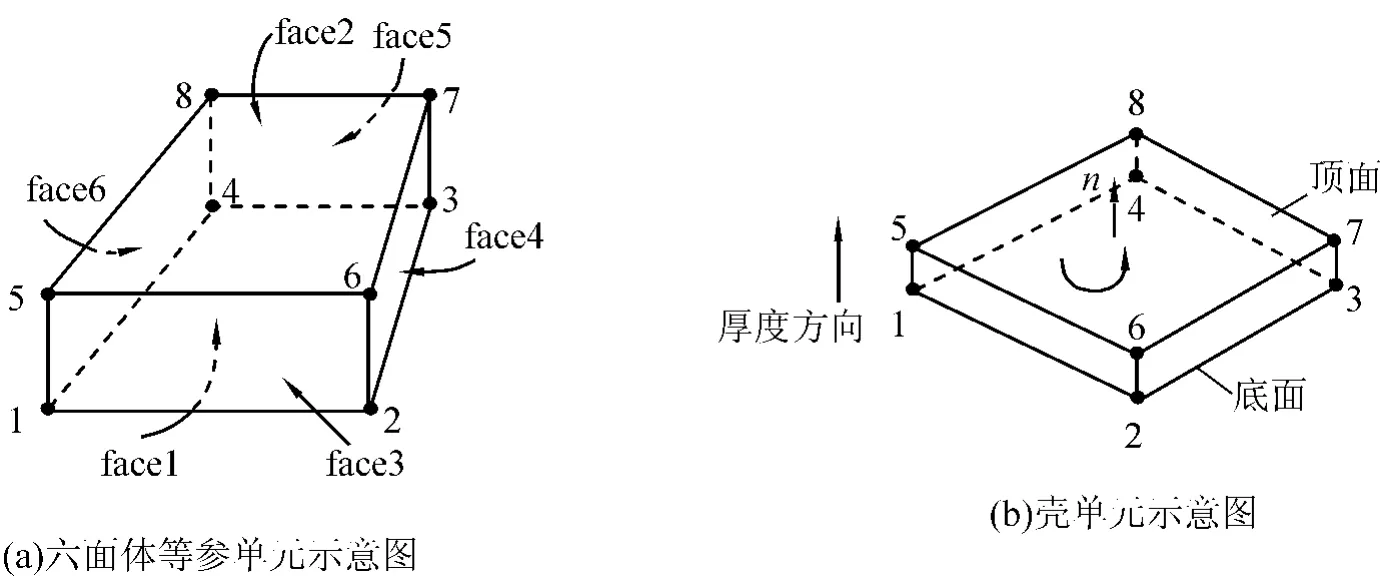
图1 计算单元示意图
(2)车辆荷载。根据桥涵设计相关规范,研究中轮胎着地压强均取0.707 MPa。为了研究路面的移动荷载,其车轮荷载下的单元划分如图2所示,图中为一车辆的车轮对铺装层所施加的荷载,从左至右分别是后轮、中轮和前轮。Abaqus采用DLOAD用户子程序来施加移动荷载,为了减少单元数目,又保证力施加的准确性,这里单元的宽度和车轮宽度一致为0.2 m。

图2 车辆荷载施加单元图
(3)本构模型及材料参数选择。为了研究车辆荷载下桥面混凝土铺装层的受力情况和破坏机理,选择以下的材料本构模型和参数:①桥梁及铺装层。基于Abaqus中的混凝土弥散开裂模型(smeared cracking)是建立在弹塑性理论框架内,用固定弥散裂纹模型模拟混凝土受拉的本构模型。因此,采用弥散开裂模型来模拟铺装层混凝土,其弹性模量为30 GPa,泊松比为0.1667,密度为2551 kg/m3。②铺装层与桥梁的粘结接触层。铺装层和桥梁面板之间采用接触问题进行分析。在Abauqs中,接触问题默认采用纯主从面(pure master-slave)接触算法,即从面上的节点不能穿过主面。因此本研究采用一个弹簧施加接触条件称为罚函数法,弹簧刚度或接触刚度k称为罚函数。
2 连续T梁桥桥面铺装层最不利荷载位置分析
滏阳新河特大桥全桥总长为2382.5 m,全桥按单向4车道设计,桥梁净宽21 m,桥梁两端各设0.5 m的防护栏。采用预应力混凝土装配式连续T梁单跨为30 m,梁高采用200 cm,共9片T梁组成,预应力混凝土按A类构件设计,并采用等梁长的直梁预制方式。选取上述滏阳新河特大桥一联连续T梁的三维实体模型如图3所示。

图3 连续T的三维实体模型
此处分析以2列×8行的车队匀速行驶对桥面进行加载,计算中车队每步前进1 m,计算结果如图4、图5所示。
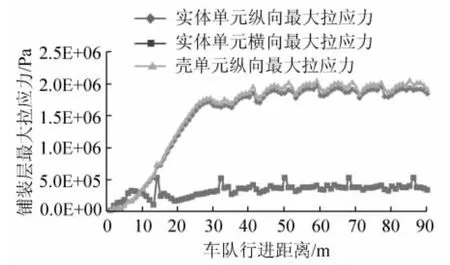
图4 车队荷载作用下铺装层纵向和横向最大拉应力曲线

图5 桥面纵轴线上铺装层表面的纵向正应力分布曲线
由图4可见采用壳单元计算得的铺装层纵向最大拉应力于实体单元非常接近,在车队行进的过程两种单元计算结果最大相差6.4%,且多数相差在5%以下,可见铺装层采用薄壳单元和实体单元计算结果非常相近,因此下文中铺装层采用实体单元进行计算。
从图4可以看出,连续T梁铺装层的最大横向拉应力明显小于最大纵向拉应力,同时也可以说明,由于连续梁负弯矩的存在使得混凝土铺装层的最大纵向拉应力要大于横向的,因此应把纵向最大拉应力作为连续梁铺装层的拉应力指标。当车辆行驶至59 m处时,铺装层的纵向最大拉应力达到最大值为1.972 MPa。
图5则是车辆行驶至59 m和90 m处,铺装层纵向中轴线上正应力的随位置的变化图。由于车辆荷载在桥墩处产生负弯矩,从而在铺装层内产生较大拉应力,在离最大拉应力最大处沿纵向前后各5 m处的拉应力值则下降均达到了一半,因此,提高铺装层离桥墩前后共10 m以内的抗拉强度指标则对桥面铺装层的整体抗拉强度有较大幅度的提高。
结合上述分析,本研究确定该连续T梁的纵向最不利荷载位置为距本文选取模型左端59 m处。
3 不同因素作用下连续T型梁铺装层的力学响应研究
主要研究水平荷载、超载、铺装层厚度以及铺装层的弹模这个四个因素下铺装层的力学响应,并根据最大纵向拉应力和最大粘结层剪应力这两个指标来描述各因素对铺装层的影响。这四个因素简述如下:
3.1 水平荷载概述
车辆在行驶过程中由于车辆的制动、轮胎与路面接触面上将会产生水平荷载。水平荷载为

式中,μ为滑动摩擦系数;P即为车辆垂直荷载。由于受路面的材料和干湿条件的影响,其滑动摩擦系数也有所不同。为了研究水平荷载对铺装的影响,本实验取水平力系数分别为0、0.3、0.5、0.7和1这五个状态进行趋势研究。
3.2 超载概述
超载模型分为两种,一种是通过改变轮胎的接地面积和另一种改变胎压而不变接地面积这两方法。由于采用改变胎压的方式模拟超载偏保守,因此本实验只改变胎压而不改变车胎接地面积,以超载系数为0~100%,每隔25%进行一次计算,表1即为不同超载系数的车辆吨位。

表1 不同超载系数的车辆载荷值
3.3 铺装层厚度概述
铺装层与桥梁粘结与一体,其厚度的不同肯定导致不同的应力状态,因此,分析铺装层厚度分别为4、6、8、10和12 cm的情况下其力学响应。
3.4 铺装层模量概述
考虑了环境温度的变化以及铺装层模量的差异,受力疲劳损伤以及老化等,铺装层的模量也不同,由于铺装层与桥梁粘结后形成一个受力整体,铺装层和桥梁的模量差异必然导致受力体的应力的不连续,本文亦取铺装层弹性模量分别为27、30、33、36和39 GPa,分析了铺装层应力响应在5种不同铺装层模量条件下的变化规律。
3.5 计算结果分析
综合以上四个因素,计算结果如图6~图9所示。

图6 不同水平荷载系数下铺装层力学响应随铺装层厚度的变化
通过逐一计算分析了超载、铺装层厚度、铺装层弹性模量以及水平荷载系数对铺装层的力学响应,现对这四个因素的影响归纳如下:
(1)水平荷载的影响。由图6(a)和图6(b)可知,铺装层的纵向最大拉应力随着铺装层的厚度增大而减小,铺装层由4 cm增大至12 cm时,纵向最大拉应力下降约20%,而铺装层的横向最大拉应力也有随着铺装层的厚度增大而减小的趋势;由图6(c)可知,铺装层垂向最大剪应力亦随着铺装厚度的增大而减少,当水平载荷系数为1时,铺装层由4 cm增大至12 cm时,铺装层的最大剪应力由0.55 MPa下降至0.372 MPa,降幅达32%;从图6(d)中可以看出,粘结层面的最大剪应力随着水平载荷系数的增大而有所增大,同时,当水平荷载系数小于或等于0.5时,最大粘结层剪应力随着铺装层的增大而增大,而水平荷载系数为0.7和1时,最大粘结层剪应力随着铺装层的增大而降低。综上所述,水平荷载对铺装层的纵向最大拉应力有一定幅度的提高,而对铺装层与桥梁间的粘结层的最大剪应力影响则更是十分明显。因此,在铺装层设计中对车辆水平荷载应重点关注粘结层的抗剪强度。
(2)弹性模量的影响。图7反映了铺装层弹性模量的不同对铺装层力学指标的影响。从图上可以看出铺装层的纵向最大拉应力随着弹性模量增加而逐级递增,且弹性模量在27~39 GPa之间每次递增3 GPa,铺装层的纵向最大拉应力递增约15%,而横向最大拉应力、垂向最大剪应力、粘结层最大剪应力随着弹性模量的递增,影响不是很大,且接近线性关系。综上所述,铺装层的模量的增大将显著增加铺装层内的拉应力水平,而在实际情况中,往往是铺装层模量越大其抗拉强度指标也相应的较大,因此,在铺装层材料的设计选择时,应在力学分析及材料试验基础上综合考虑,以保证一定模量的材料应用于铺装层,其抗拉强度亦能满足相应的要求。
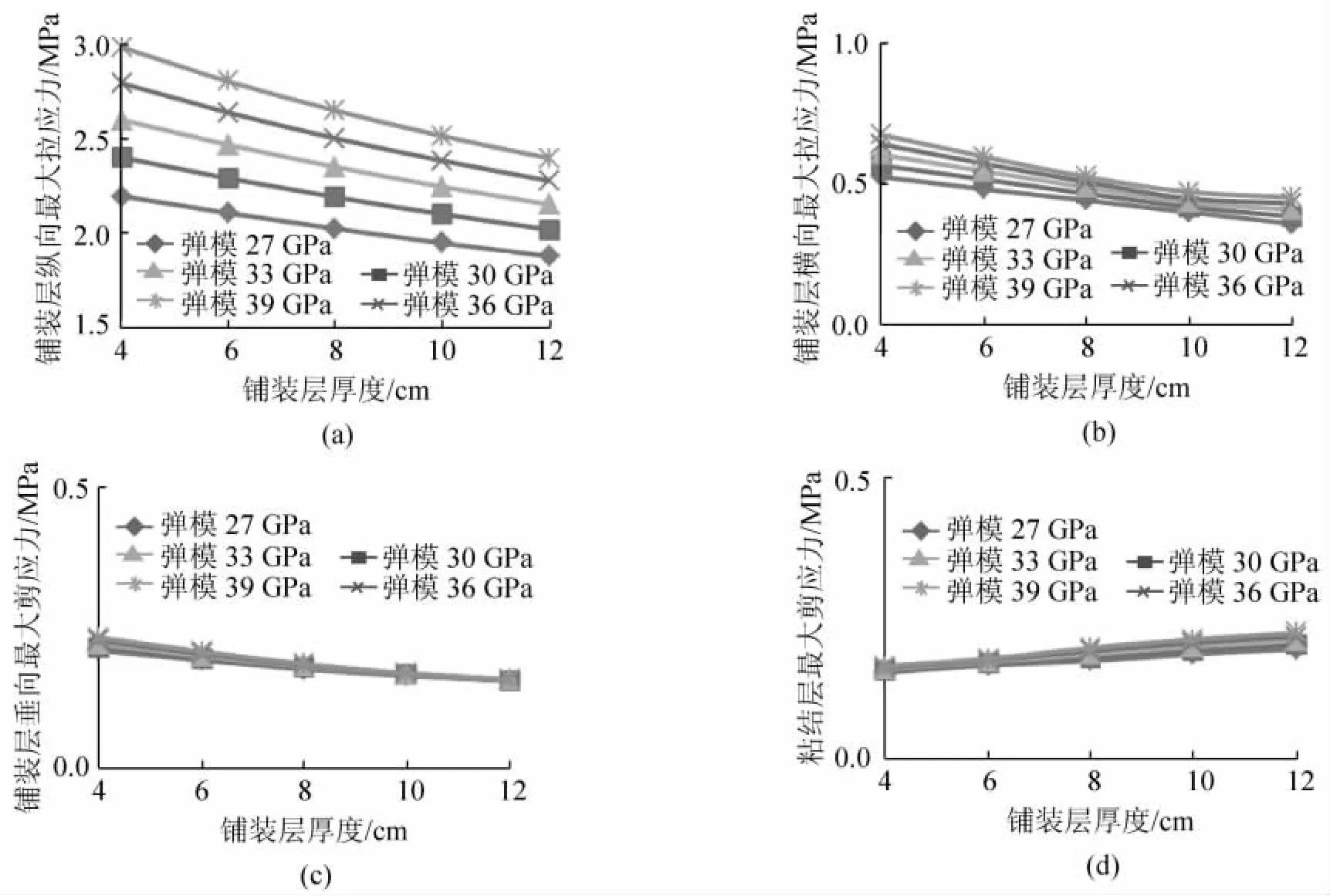
图7 不同铺装层弹模下铺装层力学响应随铺装层厚度的变化
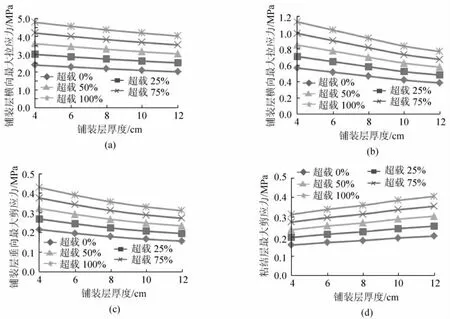
图8 不同超载系数下铺装层力学响应随铺装层厚度的变化

图9 不同水平载荷系数下粘结层剪应力对比云图
(3)超载的影响。图8反映了超载为0%、25%、50%、75%和100%对铺装层力学指标的影响。从图中可以分析得出,铺装层的各力学指标总体随着超载幅度的增加呈线性增长,以铺装层厚度不同下铺装层纵向最大拉应力变化和粘结层最大剪应力为例,如图8(a)和8(d)所示,当超载系数介于0~100%之间,越载系数每增长25%,各力学指标平均增大约20%,且不同铺装层厚度下的增幅几乎一致。因此,在实际工程中,判断超载作用下的铺装层应力指标,跟据常载荷下的应力指标和超载系数即可得出,且超载作用不受铺装层厚度等抑制。
(4)铺装层厚度的影响。从图6、图7和图8可以明显的看出,无论是超载、铺装层弹性模量还是水平载荷系数不同,铺装层的纵向最大拉应力均随着铺装层的厚度的增大而减少,相反,粘结层的最大剪应力则随着铺装层厚度增大而增大。跟据上述分析,超载作用下各力学指标为线性变化,因此在其它超载工况下亦会得到相近的结果。
综上所述,较薄的铺装层能够显著降低粘层面的最大剪应力水平,而较厚的铺装层则能在一定程度上减小铺装层的纵向最大拉应力。虽然,铺装层的纵向最大拉应力随铺装层厚度的增大减小幅度有限,但由于铺装层的纵向拉应力水平较高,因此,降低的绝对值亦较高,尤其在超载工况下,所以在实际的工程应用中,还应结合材料的实际状况,决定最合理的铺装层厚度。
4 结论
研究以大广高速公路衡大段滏阳新河特大桥为背景,采用水泥混凝土桥梁常用的连续T梁进行三维有限元分析,对混凝土铺装层在车辆荷载下力学响应进行了分析。
通过计算与分析发现连续T梁增大铺装层厚度会提高铺装层与桥梁变形不一致的趋势,导致铺装层的纵向最大拉应力减小,而粘结层的最大剪应力增大;弹性模量越大,其力学响应也大,对于连续梁在桥梁的负弯矩区,即跨端部位一定范围对,铺装层的拉应力水平较高,因此,可对这些部位进行局部补强;通过铺装层的厚度来调节车载下粘结层的应力水平能力相当有限,最根本需采用具有较强抗剪性能的粘结层;超载对于铺装层的各力学指标的影响非常显著,故应严格的控制超载车辆,保护桥面铺装层的正常使用状况。
综上所述,由于材料性能,桥梁结构设计等影响,上述分析并不能应用于每一个混凝土桥梁。因此,在铺装层设计中,应从桥梁整体的角度针对性地对桥面铺装层厚度、材料选择等进行合理的优化,保证桥梁的在运行过程中的稳定性和建造的经济性。上述研究中假定铺装层一直处于弹性状态,关于在弹塑性状态下的分析还需进步一研究。
[1]韩冬卿.高等级公路桥面铺装层破坏原因及对策[J].公路,2002(9):10-12.
[2]胡在和.沥青混凝土桥面铺装早期病害原因分析[J].中国高新技术企业,2009(2):22-25.
[3]周志刚,杨建军,刘小燕.钢箱梁桥面铺装层状体系承载力学响应[J].长沙理工大学学报:自然科学版,2007,4(1):7-12.
[4]谭茶生,曾庆敦.混凝土桥面铺装层的多重断裂分析[J].广东工业大学学报,2007,24(1):13-15.
[5]涂常卫,黎增丰,凌子如.混凝土桥面铺装病害与设计和施工的关系浅析[J].公路,1999(2):5-9.
[6]许涛,黄晓明,高雪池.移动荷载作用下沥青混凝土桥面铺装层动力响应分析[J].公路交通科技,2007,24(10):17-20.
[7]王春雷.桥面铺装破损原因及对策[J].辽宁交通科技,2003(3):33-35.
[8]熊峰,吴光蓉,肖贤德.重庆长江二桥桥面病害分析与处治研究[J].公路交通技术,2007(1):17-21.
[9]邓强民,倪富健,顾兴宇,等.钢桥面铺装非均布轮载效应分析[J].东南大学学报:自然科学版,2007,37(4):15-18.
[10]黄朝晖.桥面混凝土铺装层病害处理对策[J].工程与建设,2008(3):27-30.
[11]顾兴宇.悬索桥桥面沥青铺装层力学分析及结构设计研究[D].南京:东南大学交通学院,2002.

