采用加速度输入等效风力发电机组塔筒实测响应方法研究
冯又全, 陈俊岭
(同济大学 建筑工程系,上海 200092)
0 引言
随着风力机大型化的发展,更大的叶轮直径和更高的塔架已成为风电发展的主流趋势。在风力发电机组整体结构中,由于风电机组的主要部件全部安装在塔架顶端,塔架一且发生倾倒垮塌,往往造成整个机组报废。与其他高耸结构相比,风力发电塔的工作条件、设计因素更加复杂,对设计起控制作用的风荷载对环境作用具有典型的随机性,风速风向的不稳定性导致机组运行时塔筒所受的影响是动态随机的。塔架作为重要的支承部件,不但要抵抗风作用在桨叶上的力和力矩,还要承受由于风速、风向变化以及发电机偏置等因素引起的塔架振动。塔筒振动的最大危害就是使塔筒连接部位和其上的某些机舱构件产生疲劳,塔架材料的强度大大降低,缩短塔架使用寿命。要保证风力机安全、平稳、高效地运转,振动问题是塔架设计考虑的主要因素之一,因此风力发电机组塔筒的振动控制研究引起越来越多学者的关注。
目前,对于结构物的振动控制研究可采用理论分析、数值模拟和现场实测等方法,对减振装置控制的效果一般通过对比现场实测进行验证。对于各种控制装置的有效性,国内外的很多学者通过理论分析和数值模拟的方法验证了一点,例如文献[1]~文献[4]研究了各种减振器控制参数的最优取值;文献[5]通过对合肥电视塔风振响应分析,得出具有最优参数的TMD可以降低塔楼处的加速度响应,显著提高电视塔的人体舒适度性能。但是采用试验方法验证各类减振器控制效果的文献较少,例如文献[6]采用理论和试验相结合的方法对将要安装到捷克某两座电视塔上的滚球减振器进行分析,得到该减振器和结构自振频率相对应的简谐荷载激励下的控制效果;文献[7]对上海环球金融中心大厦现场阻尼装置开启和关闭进行测试,得到阻尼装置对风振效应和整体结构阻尼比的控制效果。
采用试验方法研究结构的风致效应,多采用风洞试验的方法,但是受雷诺数缩尺效应、气弹效应和测试方法本身的局限等多种因素的影响,使得基于风洞试验的风荷载模拟与实际结构上的风荷载存在不可忽视的差异。风力发电塔架在额定风速、极限风速和切出风速作用下的结构响应和一般建筑物的风致响应显著不同,仅对塔架进行振动控制模型实验时,叶片过速切出工况在风洞实验中很难实现。但振动台试验中加速度的输入具有可控性、稳定性和可重复性,例如文献[8]设计并完成了考虑土与结构相互作用的结构减振控制大型振动台模型试验,得到土与结构相互作用具有降低和提高结构减震控制效果的双重作用,使得基于刚性地基假定条件下设计的TMD减震控制系统在柔性地基条件下的控制效果不太理想。基于振动控制研究的现状,基于随机振动和系统识别理论,对某风力发电塔的风致效应进行研究,使得从基底输入加速度时塔筒的动力响应与已知风荷载作用下的响应一致,从而使得在振动台上完成对风力发电机组塔筒的风致响应控制试验成为可能。
1 加速度与风荷载的等效方法
1.1 单自由度体系
对于图1所示顶端作用有集中质量m的悬臂柱,其抗弯刚度为k,柱高度为h,假设在顶端风荷载p(t)作用下,柱顶的水平位移为u(t),基底弯矩为M(t),质点m的运动方程可表示为

当从图1受示悬臂柱的基底输入¨ug(t)的加速度时,质点的运动方程为
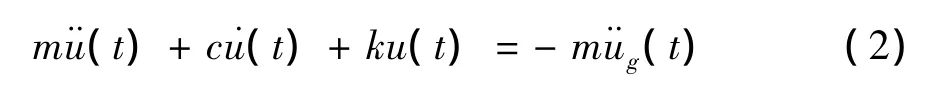
由此可见,若使得悬臂柱在风荷载p(t)作用下基底弯矩和基底输入¨ug(t)的加速度产生的基底弯矩等效,则风荷载和加速度之间需满足

因此在风荷载p(t)已知的情况下,输入的加速度¨ug(t)可直接求得。
已知的基底弯矩M(t)与柱顶水平位移u(t)的关系为:M(t)=ku(t)h,因此,柱顶位移与基底弯矩具有相同的波形。将ω2=k/m,ζ=c/2mω代入式(2),经变换得到
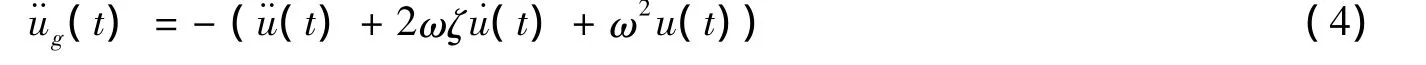
因此求等效基底加速度输入就变为质点加速度¨u(t)、位移响应乘以结构圆频率的平方ω2u(t)与速度响应乘以阻尼比2ωζ˙u(t)三项的叠加,其中u(t)=M(t)/kh,而加速度响应¨u(t)和速度响应˙u(t)可通过对位移响应分别求两阶和一阶导数得到。
1.2 广义单自由度体系
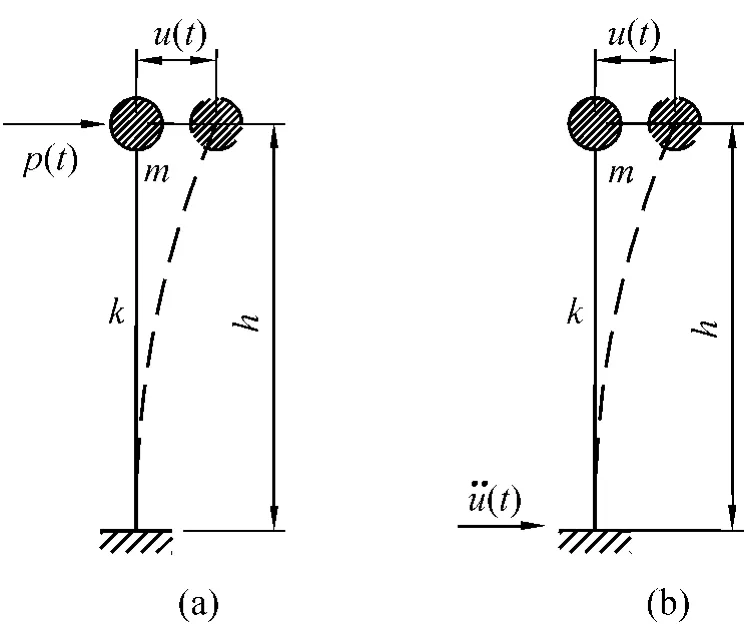
图1 单自由度体系示意
对于图2所示风力发电塔,叶片和机舱可以简化为塔顶端的集中质量,塔筒沿高度方向为变截面、变厚度的无限自由度体系。对此类细长结构,风荷载作用下弯曲变形形式单一,振动位移沿塔高的分布基本符合一阶振型,因此可简化为广义单自由度体系。假定一阶振型形状函数为φ(x),相对于基底的运动振幅为广义坐标Z(t),根据文献[9],其运动方程为


图2 风力发电塔(单位:mm)
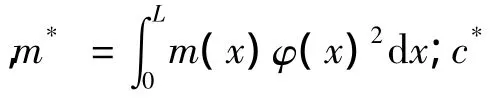
2 实例分析和有限元验证
图3为风机叶片过速刹车工况下的基底弯矩时程曲线,基底弯矩在约37.5 s时叶片刹车后进入自由振动阶段。通过加速度输入在振动台上完成对已知效应的模拟需要对实测所得弯矩时程的初始条件进行处理,使得修改后的弯矩时程满足M(0)=0和¨u(0)=0的初始条件,并在交接处与原弯矩时程形状基本吻合,对图3所示弯矩时程即在初始数据之前添加了3.52 s的初始激励。通过对弯矩时程M(t)的离散傅里叶变换得到其功率谱密度曲线(见图4),可见该风力发电塔基底的动力响应以一阶振动为主,振动频率为 0.228 Hz。
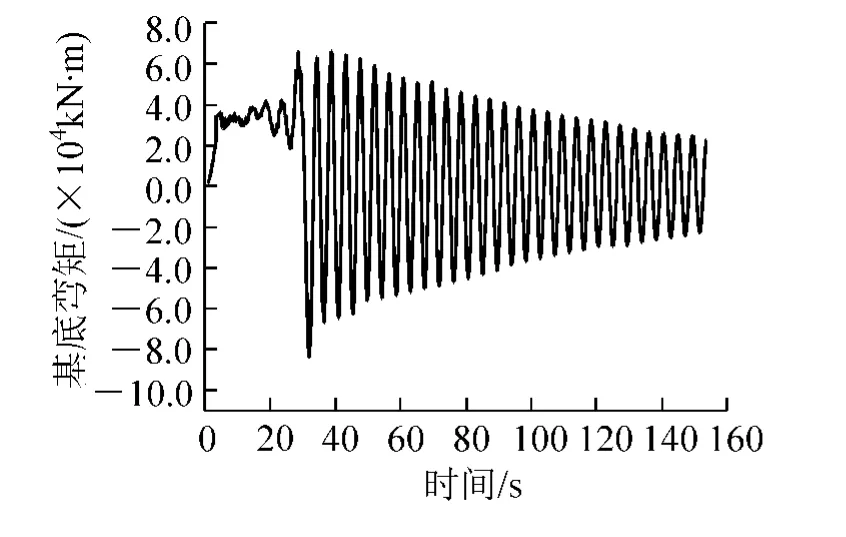
图3 已知的基底弯矩时程曲线
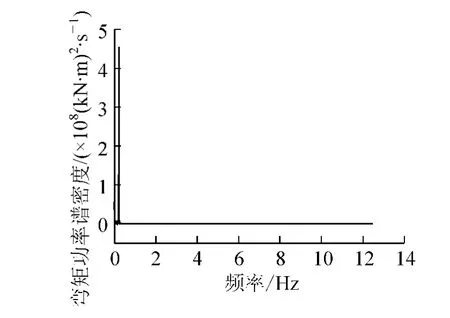
图4 基底弯矩的功率谱密度
运用SOLVIA有限元软件,用Beam单元对图2所示风塔建立有限元模型进行模态分析求得总模型质量524 t,塔身质量404 t(包括附属物),对应第一振型的模态质量m*=167.3 t,塔顶的集中质量120 t(包括机舱、叶片等设备重)占第一振型模态质量167.3 t的70%以上;广义刚度为 k*=m*ω2=3.433×105kN/m。
2.1 差分法
将基底弯矩M(t)、广义联合刚度 k*和塔高h代入u(t)=M(t)/ k*h,得到塔顶的位移时程u(t)。根据动力学基本原理,质点的加速度时程和速度时程可分别通过对位移时程的二阶和一阶导数求得,当质点的位移时程已知并用有限个离散的点表示时,加速度和速度可近似分别由对位移时程u(t)的一阶差分和二阶差分求得。由于外界干扰或仪器采集频率等因素的影响,采集到的信号并非理想的光滑曲线,在某些点处出现尖锐点,因此差分前可采用Savitzky-Golay算法对信号数据进行平滑处理,以此避免直接差分过程中产生奇异点,图5(a)~(c)分别为组成等效基底加速度的三项分量¨u(t)、2ωζ˙u(t)和ω2u(t)。
由图5(d)可以看出,合成的基底等效加速度中仍存在高频分量,需通过滤波剔除。通过傅里叶变换做出加速度功率谱密度曲线,判断出滤波的截断频率在0.3~0.4 Hz之间,具体取值可将滤波后的加速度输入有限元模型中验证微调。最终选定截断频率为0.3843 Hz,剔除高频信号后,利用傅立叶逆变换对低频信息进行变换,得到剔除噪声之后的响应信号,并使得37.5 s之后的加速度激励为零(见图6)。
2.2 三角谐波叠加

图5 合成的等效加速度

由此速度˙u(t)时程和加速度时程¨u(t)可直接通过式(6)求一阶和两阶导数,表达为
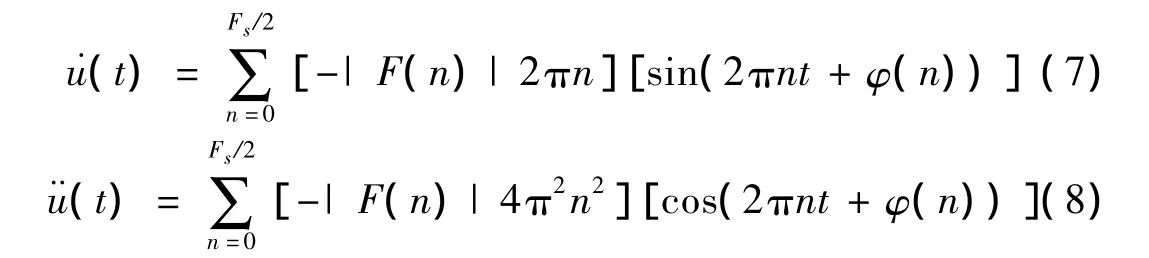
由式(7)和式(8)可知,速度时程˙u(t)与位移时程u(t)有90°的相位差,频域幅值与位移频域幅值相差 -2πn;加速度时程与位移时程u(t)相位相同,其频域幅值为速度频域幅值的-4π2n2倍。采用谐波叠加和直接差分法求等效基底加速度的不同在于,前者将位移表达为谐波叠加形式后,速度和加速度时程可直接求导,后者为直接差分。二者在计算过程中均需要采用去噪方法对信号进行处理,滤波后逆傅里叶变化得到等效基底加速度,所得结果非常接近。
2.3 有限元分析验证
将滤波后所得的等效加速度作为基底加速度,用SOLVIA软件进行动力非线性分析,得到塔底的弯矩时程曲线,并与实测所得的时程曲线进行比较(图7(a))。从图中可以看出,用等效后的加速度输入得到的弯矩时程和实测的时程非常吻合。
风力发电塔在正常运行过程中,基底的弯矩时程如图7(b)所示。在该工况下,同样可以采用上述方法求得等效的基底加速度,只是滤波时采用的带宽有所不同。经有限元分析验证,虽然局部响应有些差异,但是总体来看等效后的基底加速度可以较好的模拟脉动风激励。

图6 等效基底加速度
3 结论

图7 基底弯矩对比
通过单自由度体系运动方程的分析,得到塔顶位移和已知基底响应之间的关系。由此类推,通过对风力发电塔的模态分析,求得其第一振型的广义质量和广义刚度,由此将已知弯矩时程进行反演,得到产生相等响应的等效基底加速度。通过用有限元软件SOLVIA计算得到在此激励下,塔柱的底部弯矩。通过对比可知,对于风力发电塔这类以一阶振型为主的结构体系,可以通过效应等效的方法,将作用在结构上的风荷载激励等效为从基底输入的加速度,从而使得在振动台上完成振动控制实验成为可能。
[1]L Zuo,S A Nayfeh.Minimax optimization of multi-degree-of-freedom tuned-mass dampers[J].Journal of Sound and Vibration,2004(272):893-908.
[2]Giuseppe Carlo Marano,Rita Greco,Bernardino Chiaia.A comparison between different optimization criteria for tuned mass dampers design[J].Journal of Sound and Vibration,2010(329):4880-4890.
[3]Chien Liang Lee,Yung Tsang Chen,Lap Loi Chung.Optimal design theories and applications of tuned mass dampers[J].Engineering Structures,2006(28):43-53.
[4]Steen Krenk,Jan Høgsberg.Tuned mass absorbers on damped structures under random load[J].Probabilistic Engineering Mechanics,2008(23):408-415.
[5]蔡丹绎,涂幼麟,李爱群,等.合肥电视塔TMD风振控制的响应分析[J].工程力学,2001,18(3):53-60.
[6]Miro Pirner.Actual behaviour of a ball vibration absorber[J].Journal of Wind Engineering and Industrial Aerodynamics,2002(90):987-1005.
[7]吕西林,李培振,郭献群,等.上海环球金融中心大厦振动控制及现场实测分析[J].结构工程师,2009,25(4):63-70.
[8]陈国兴,王志华,宰金珉.考虑土与结构相互作用效应的结构减震控制大型振动台模型试验研究[J].地震工程与工程振动,2001,21(4):117-127.
[9]Clough R W ,Penzien J.Dynamics of structures[M].Berkeley Calif:computers and Structures Inc.,2004.

