裂隙岩体隧道非均质、各向异性等效渗流模型及应用

刘志春， 高新强， 朱永全

(石家庄铁道大学土木工程学院，河北 石家庄 050043)

0 引言

随着可持续发展战略的深化，隧道工程所引起的地下水环境问题逐渐引起人们的高度重视，隧道工程建设与运营常导致地下水位下降、地下水资源流失及水文循环失衡，从而引起生态及生活环境恶化［1-3］。对于隧道工程与地下水的相互作用问题，以往研究大多集中在地下水对隧道工程的影响及对策，如防排水原则、结构形式、外水压力处理及人工降水引起的地面沉降等研究［2-5］，而隧道工程对地下水环境的影响方面研究较少，且大多限于隧道涌水量的预测研究方面，个别开展的隧道工程对地下水环境影响研究也仅处于定性及半定量阶段［1，6，7］。

在如何有效地评价隧道对地下水环境的影响问题上，建立切实可行、行之有效的裂隙岩体渗流模型显得尤为重要。裂隙岩体的渗流模型，根据岩体裂隙特征和裂隙性质的把握准确程度，主要为等效孔隙(连续)介质模型、双重介质模型和网络裂隙介质模型等［8］。然而，裂隙岩体本身具有复杂性，其渗流特征具有多样性，计算模型如要完全反映裂隙岩体的渗流特征基本上是不可能的。因此采用等效连续介质模型，旨在研究如何进行模型假定、边界条件选取、模型材料选择、参数选取等，才能较好地反映裂隙岩体隧道的渗流特征。

1 裂隙岩体的渗流特征

(1)岩体的裂隙性。裂隙介质是相对于孔隙介质和溶穴介质，是指含裂隙水的岩体。裂隙岩体由于裂隙发育、分布的方向性和不均匀性，其渗透具有明显的各向异性和不均一性特点。

(2)岩体的渗透性。水只能沿连通孔隙或裂隙渗透，岩体渗透性大小主要取决于岩石孔隙的大小、方向及其相互连通情况，用渗透系数来衡量。

(3)岩体渗流的不均匀性。是指在岩体空间内，不同位置上渗透系数大小不同。宏观岩体渗流不均匀性主要是由于不连续面的发育程度的差异，通常表现为分带性和成层性。

(4)岩体的各向异性。由于岩体介质具有非均质各向异性，要用渗透张量来描述岩体介质各个方向上的不同渗透性能。通常在节理裂隙密集展布的方向上，岩体的渗透性占主导优势。一般经过坐标变换的各向异性为非轴向各向异性。

除此，裂隙岩体还具有非饱和性及耦合特性等［8-9］。

2 裂隙岩体渗流模型

(1)等效连续介质模型是把岩块-裂隙系统等效成连续介质，用连续介质理论描述渗流方程，认为水流服从Darcy定律，可直接应用孔隙介质渗流理论，操作性好。

(2)双重介质模型也是一种连续介质模型，认为岩块孔隙系统(包括微裂隙)和裂隙系统连续地充满整个区域，即把裂隙岩体看作是具有不同水力参数的两种连续介质的叠加体，两种连续介质中的渗流场均建立在Darcy定律的基础上，并依据两种介质间的水交换项来联立求解各自的渗流场。

(3)网络裂隙介质模型认为岩块本身不透水，整个地下水运动是通过裂隙网络来进行的。

由于裂隙本身的复杂性，后两种模型在解决实际工程问题时均有其局限性。

3 流体偏微分方程

模型采用GeoStudio软件SEEP/W模块，该模块用于分析土体或岩体地下水渗流和超孔隙水压力消散问题［10-11］。二维渗流偏微分方程通常可表述如下

式中，H为总水头;Kx为x方向的水力渗透系数;Ky为y方向的水力渗透系数;Q为应用边界通量;θ为单位土体中含水量的变化;t为时间。

该方程说明了在某一时刻点流进和流出一个单元体流量通量的差等于土体中含水量的变化。更具体的说，单位时间内，在x和y方向及外表面方向通量总的变化速率等于单位土体中含水量的变化率。

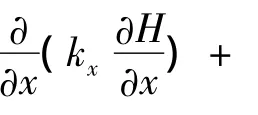
体积水含量的变化取决于土体应力状态和特性的变化。在饱和土和非饱和土的条件下，应力状态用两种状态变量来描述。这些应力状态变量分别是(σ－ua)和(σ－uw)，这里σ是总应力，ua空隙气压力，uw空隙水压力。

SEEP/W程序假设总应力恒定，也就是说，对土体既没有加载也没有卸载。SEEP/W还假定:在瞬态处理过程中，空隙气压力为定值且等于大气压力。这意味着(σ－ua)保持为定值，对体积含水量的变化没有影响。含水量变化相应地仅仅取决于(σ－uw)状态变量的变化，其中，ua为定值，含水量的变化仅是于空隙水压力的函数。结果是，含水量的变化仅与空隙水压变化有关，如式(2)所示

式中，mw为含水量曲线的斜率。总水头H可以这样定义

式中，uw为空隙水压;γw为水容重;y为位置水头。

4 裂隙岩体隧道非均质、各向异性等效渗流模型

采用SEEP/W模拟软件建立等效连续介质水文地质模型，为增加模型拟真性，在模型中考虑岩层的非均质性、非轴向各向异性［12］。

4.1 模型材料

模型材料中按实际地层厚度取值，考虑材料的非均质性。根据结构面分布情况，考虑平行于结构面方向的渗透系数为Ky'，垂直于结构面方向的渗透系数为Kx'，定义各向异性特征系数Kr=Ky'/Kx'。Kr的取值与节理发育程度紧密相关，结合以往经验，Ⅱ、Ⅲ、Ⅳ、Ⅴ级围岩Kr分别取值为10、50、100、500。

计算断面选取为垂直于隧道轴向横断面，岩层结构面真倾角转化成结构面在计算断面处的视倾角γ=arctan(tan αsin(90°－β))，其中，α为岩层结构面(真)倾角;β为岩层结构面倾向。

4.2 材料参数

对于稳态分析，材料参数主要为包括渗透系数K、结构面视倾角γ、各向异性特征系数Kr。围岩渗透系数K取值根据施工期间实测涌水量，以及水井水位监测结果通过经验公式及数值模型反演确定。帷幕注浆及径向注浆所形成的注浆圈渗透系数按围岩水泥注浆效果试验经验统计取值。喷射混凝土渗透系数按设计抗渗等级、实际施工效果试验和经验统计按P2抗渗等级取值。二次衬砌模筑混凝土渗透系数按设计抗渗等级P8取值。盲管渗透系数按砂砾石渗透系数取值。结构面视倾角γ根据实际结构面倾向及倾角计算确定。Kr按围岩分级确定。

4.3 模型边界取值范围

计算模型上边界为隧道施工前初始地下水位线，下边界根据隧道埋深情况取隧道底面以下50～100 m。左、右边界根据地形情况、地质情况选择确定，其选取原则为:

(1)分水岭位置作为模型左、右边界;

(2)断层结构面位置做为模型的左、右边界;

(3)河流及水库位置做为模型的左、右边界;

(4)如地面较平坦，无上述各种边界，可根据影响半径的经验公式［13］取值，即R=215.5+510.5K，其中，R为隧道涌水影响半径;K为岩体渗透系数。

4.4 边界条件

稳态分析中，左、右边界采用定水头边界条件，其水头等于边界处水位高度;下边界为不透水边界。

上边界，即隧道施工之前的初始地下水线，隧道施工排水后，其水头(负压力水头)是未知的，其流量在地形及地下水位起伏较大时也是未知的，只有在地形及地下水位水平时上边界流量均为0(不考虑降雨入渗因素)。此时，对于上边界可采用q=0(或Q=0，q为单元流量，Q为节点流量)潜在浸润面检验边界，也即通过迭代求解找出浸润面位置。当考虑降雨入渗时，可按当地年降雨量和降雨入渗系数，计算出每天的降雨入渗量，然后可设q=定值的潜在浸润面检验边界。对于隧道洞壁边界条件可设为压力水头为0，或同样采用检验的潜在浸润面q=0边界，二者是等效的。当然也可以根据需要设为固定流量边界。

5 应用实例验证

石板山隧道位于石太客运专线河北省井陉县之内，设计为单洞双线隧道，最大埋深322 m，全长7505 m，隧道开挖最大跨度近15 m，起讫里程DIK49+585～DIK57+090，是全线的重点控制工程。隧道工程区属于太行山东麓基岩低山区，属于北方干旱、半干旱区，降水量不大，地表植被较发育。隧道范围地层主要岩性为第四系上更新统坡洪积层(Q3dl+pl)新黄土，碎石类土，冲洪积层(Q3al+pl)粉质黏土;寒武系中统徐庄组(ε2x)泥质条带灰岩、页岩、石灰岩，寒武系下统毛庄组(ε1mz)白云岩、白云质泥岩;元古界长城系高于庄组(Chg)白云岩、长石石英砂岩，大红峪组(Chd)石英岩状砂岩、长石石英砂岩夹粉砂岩，甘陶河群变长石石英砂岩、云母片岩、绿泥片岩;太古界南营岩组(Arn)花岗片麻岩;局部为燕山期(δu)辉绿岩侵入体。地下水分为变质岩风化裂隙水、碳酸盐岩岩溶裂隙水、松散层孔隙水，以及碎屑岩夹碳酸盐岩孔隙裂隙岩溶水。地下水主靠大气降水直接渗入及基岩山区地下水径流的侧向补给。

隧道区范围内分布有多处泉、井和水库。隧道施工过程中，曾造成井泉干涸，水库水位下降，影响到居民的生产生活用水。施工中采取帷幕注浆、补充径向注浆、全包式柔性防水层、提高喷射混凝土防水性能、及时支护封闭等系列防排水技术体系。合理评价隧道对地下水资源的影响显得尤为重要。

沿隧道纵向选取14个代表性断面进行渗流分析，建立计算模型分析隧道施工引起的地下水渗流规律，并得出地下水位变化及地下水资源流失量，如图1为DIK52+300断面计算模型。在未考虑降雨季节变化情况下，得隧道运营阶段分区段排水量分布如图2所示。

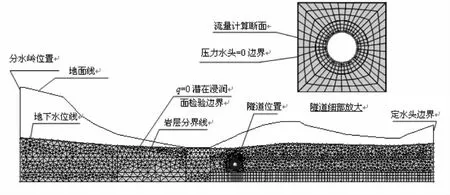
图1 DIK52+300计算模型

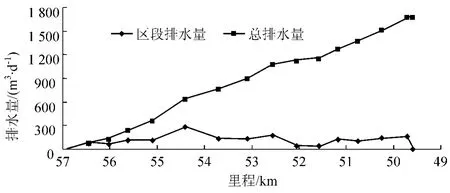
图2 成洞运营阶段分区段隧道排水量

由图2，DIK51+800、52+300代表区段按实际施作帷幕注浆考虑，其余区段采用常规复合式衬砌，得运营阶段隧道总排水量为1669.74 m3/d。从图中区段排水量曲线可见，施作帷幕注浆区段排水量明显下降，说明帷幕注浆是防止地下水资源流失的有效手段。2008年8月28日和10月9日雨季两次测试的隧道总排水量分别为2082.24 m3/d和1607.04 m3/d。计算结果与实测结果较为吻合，但计算结果未考虑降雨季节变化，两次实测为雨季测试，故计算结果实际上比实测结果略偏大。

6 结语

(1)采用非均质、各向异性等效连续介质模型模拟裂隙岩体渗流规律及地下水资源流失量，并应用于实际工程中，计算结果较为符合实际。

(2)帷幕注浆区段排水量明显下降，是防止地下水资源流失的有效手段。

(3)计算石板山隧道运营期间隧道排水量1669.74 m3/d，说明隧道建设对区域地下水资源有一定影响，运营期间应采用有效措施进行地下水资源的合理再利用。

［1］刘丹，杨立中，于苏俊.华蓥山隧道排水的生态环境问题及效应［J］.西南交通大学学报，2001，36(3):308-313.

［2］刘志春.地铁施工与地下水渗流的环境效应分析及应用［D］.石家庄:石家庄铁道学院交通工程系，2003.

［3］高新强.高水压山岭隧道衬砌水压力分布规律研究［D］.成都:西南交通大学土木工程学院，2005.

［4］黄涛，杨立中.渗流与应力耦合环境下裂隙围岩隧道涌水量的预测研究［J］.铁道学报，1999，21(6):75-80.

［5］王秀英.岩溶隧道堵水限排衬砌外水压力及结构设计研究［D］.北京:北京交通大学土木建筑工程学院，2005.

［6］蒋忠信.隧道工程与水环境的相互作用［J］.岩石力学与工程学报，2005，24(1):121-127.

［7］肖了林.隧道修长对区域地下水位的影响分析［J］.公路隧道，2000(1):43-52.

［8］周志芳.裂隙介质水动力学原理［M］.北京:高等教育出版社，2007.

［9］林学钰，廖资生，赵勇胜，等.现代水文地质学［M］.北京:地质出版社，2005.

［10］中仿科技.专业高效的岩土工程设计分析软件 GeoStudio［EB/OL］.［2011-2-26］.http://geostudio.cntech.com.cn/intro.html.

［11］JOHN KRAHN.Seepage Modeling with SEEP/W［EB/OL］.［2011-2-26］.http://www.geo-slope.com.

［12］刘志春.干旱山区隧道施工地下水环境保护技术研究［R］.石家庄:石家庄铁道大学，2010.

［13］朱大力，李秋枫.预测隧道涌水量的地下水动力方法［J］.铁路地质与路基，1995(4):32-37.