自耦式12脉波整流系统平衡电抗器临界值设计
马彦林,何礼高,杜恩利,李旭
(南京航空航天大学 自动化学院,江苏 南京 210016)
自耦式12脉波整流系统平衡电抗器临界值设计
马彦林,何礼高,杜恩利,李旭
(南京航空航天大学 自动化学院,江苏 南京 210016)
在自耦式12脉波整流系统中,平衡电抗器是整个系统的关键器件。首先对自耦式12脉波整流系统平衡电抗器等效电路进行了详细分析,得出平衡电抗器电感和电路其他参数之间的关系。在考虑了移相变压器激磁电流对平衡电抗器激磁电流影响的因素下,提出了平衡电抗器临界值选取简单而有效的方法,仿真和实验证明了理论分析的正确性。根据该方法计算的临界电感值具有足够精度,可以满足工程需要。平衡电抗器的体积也能够进一步减小。
平衡电抗器;自耦移相变压器;多脉波整流;临界电感
1 引言
多脉波整流指在一个三相整流电源系统中,输出直流电压在一个交流周期内多于6个波头。多脉波整流系统以结构简单,可显著提高功率因数和可靠性高等优点,在大功率整流系统中具有广泛的应用价值,国内外许多学者自20世纪80年代末以来对多脉波整流技术开展研究。1995年美国学者Derek A.Paice提出了以自耦变压器代替隔离式变压器的方法后[1],多脉冲整流装置体积大大减小,引起航空、采矿、运输等众多应用领域的关注。文献[2]对自耦式12脉波整流装置进行了初步分析,随着研究的深入,甚至提出了24,30脉冲的自耦变压整流装置,并提出了对称式和非对称式多脉波整流的实现方案,采用对称结构的自耦式12脉波整流结构简单,在同等容量条件下自耦变压器比隔离变压器体积更小,且性能满足大多数场合对电流谐波的要求,因此运用较为广泛。文献[3]对自耦式12脉波整流器的工作原理、输入电流特性、输出电压特性和移相变压器的等效容量进行了详细的理论分析。文献[4]对移相变压器等效电路、平衡电抗器及激磁电流产生的原因进行分析,提出了实现均流的控制方法。文献[5]给出了12脉波自耦移相变压器的设计过程,并对不对称式多脉波整流进行了详细的分析。文献[6]分析了输入电压不平衡对自耦式12脉波整流系统的影响,提出了利用谐波抑制电抗器以减小输入电流谐波的方法。
从众多文献来看,对自耦式多脉冲整流的研究重点,主要集中在自耦移相变压器的分析和新型拓扑结构的研究上,而对关键部件—— 平衡电抗器的研究不足。平衡电抗器在电路中主要起到均压、均流的作用,保证了输出电压12脉波的合成,并降低输入电流总谐波含量。合理的平衡电抗器设计可以提高并联桥臂的利用效率。文献[7]建立了自耦式12脉波整流的非线性仿真模型,并对平衡电抗器在不同参数的情况下进行仿真分析,但未给出具体的电感设计方法。文献[5,8]给出了平衡电抗器电感量的估算方法,该电感量要保证平衡电抗器能在所规定的最小负载电流情况下能正常工作,但其计算时只考虑了平衡电抗器3次谐波电压,忽略了平衡电抗器直流电阻的影响,因此计算误差较大,在实际工程运用中往往要经过多次的调整才能保证平衡电抗器的设计达到最佳。
平衡电抗器电感量的选取,关系到两组并联整流桥之间的均流效果,若选取过大,虽然能获得更好的均流效果,但无形中增加了平衡电抗器的体积和重量,损耗随之也增大;若选取过小,则均流效果变差,12脉波整流的正常工作区间变窄。因此电抗器设计的主要工作,即先确定平衡电抗器激磁电流的设计指标,进而求出与激磁电流设计指标一致的电感量,即平衡电抗器临界电感。
综上所述,为了更准确计算平衡电抗器临界值,主要从自耦式12脉波整流的关键器件 —— 平衡电抗器的端电压分析入手,推导出平衡电抗器激磁电流表达式,在考虑移相变压器激磁电流的影响下,给出了一种平衡电抗器临界值的设计方法。
2 系统构成
该系统主电路由自耦移相变压器、2个三相二极管整流桥及2个平衡电抗器组成,如图1所示。输入三相电压(Va,Vb,Vc)经过移相变压器产生两组三相电压(Va′,Vb′,Vc′)、(Va″,Vb″,Vc″)。两组三相电压分别连接到整流桥,整流桥输出通过平衡电抗器并联连接到负载。
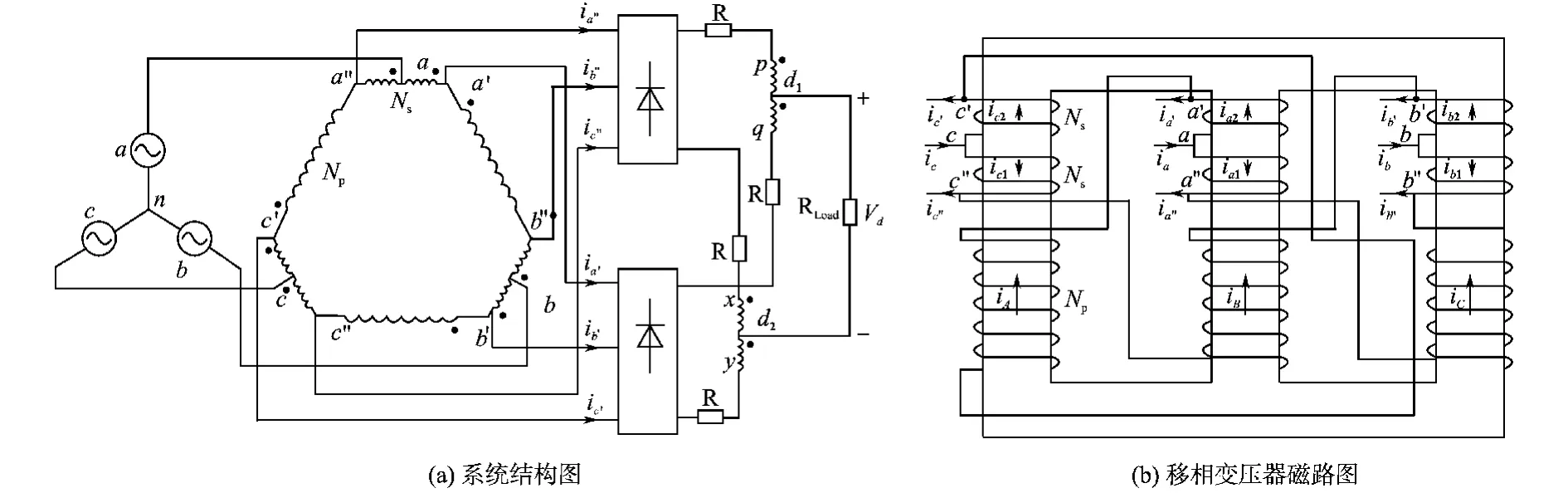
图1 自耦式12脉波整流系统Fig.1 12-pulse autotransformer phase shift AC/DC converter
移相变压器绕组采用多边形联结,每相有3个绕组,绕组同名端如图1所示。为了使整流桥输入相电压Va′,Vb′,Vc′和Va″,Vb″,Vc″之间相位相差30°,以满足12脉波整流的要求,按图1所示移相变压器连接方式,则Va″,Vb″,Vc″超前Va,Vb,Vc15°,Va′,Vb′,Vc′滞后Va,Vb,Vc15°,满足该移相关系的移相变压器长短绕组匝比为[3]

根据移相变压器电压向量图,可得到三相整流桥输入侧电压有效值:
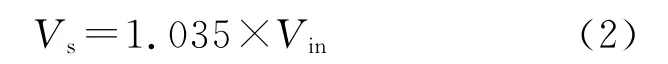
式中:Vin为三相输入电压有效值。
3 平衡电抗器分析
两个直流电源并联时,只有当电压平均值和瞬时值均相等时,才能使负载均流。12脉波整流电路中两组三相整流桥输出电压平均值相等,但瞬时值不等。如果不加均衡电抗器,任何瞬间,只有两相间线电压最高的一组整流桥上下桥臂的二极管才能导通。而平衡电抗器对瞬态电压的作用,使每组三相整流桥臂能够在同一时刻均有2个二极管处于开通状态,共同为负载提供电流。由于平衡电抗器两端(p,q或x,y)存在交流电压,因此在电抗器绕组中便会存在交流电流,此电流为平衡电抗器的激磁电流,其大小等于两绕组电流之差[9]。
平衡电抗器电感的选取,关系到系统的整体电气性能指标,若电感选取较小,则激磁电流过大,此时若负载电流小于平衡电抗器激磁电流,平衡电抗器将失效,整流桥二极管发生交叉导通的情况,每对开关管的实际导通角小于120°[5]。若电感选取过大,则无形中增大了平衡电抗器的体积重量,因此为了准确计算临界电感,首先要准确分析平衡电抗器电感量和电路其他参数之间的关系。
为使分析简化,做如下假设:
1)平衡电抗器两绕组全耦合,即耦合系数为K=1;
2)为了简化计算,文中忽略了自耦移相变压器漏感的影响,而实验表明结果并不因此而变坏;
3)移相变压器输入为三相对称正弦电压源。

3.1 平衡电抗器输入端电压
如图2所示,Lp1和Lp2为2个输出平衡电抗器,d1和d2分别为平衡电抗器的2个中点,负载跨接于电抗器的2个中点之间,并且平衡电抗器的左右两绕组关于中点对称即结构和电气参数完全一致。Rp为平衡电抗器线圈内阻。等效电路电压参考点为三相输入中性点n。

图2 整流系统输出侧等效电路Fig.2 Equivalent circuit of rectifier output side
根据三相半波整流的输出电压特性,我们可得到等效电路中各点的电压表达式。其中,超前移相绕组整流输出端电压Vpn(t),Vqn(t)及滞后移相绕组整流输出端电压Vxn(t),Vyn(t)表达式见文献[10]。
则正输出端Lp1的电压,
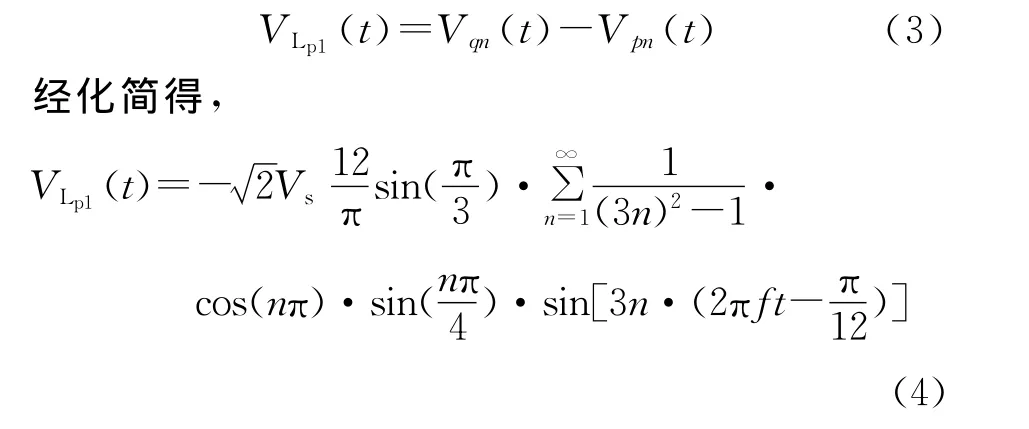
同时,负输出端Lp2的电压,
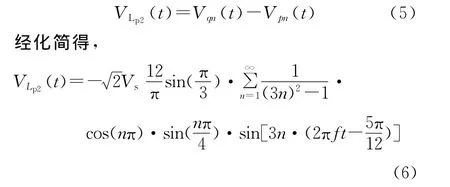
从电抗器两端电压表达式可以看出,其主要成分是3次,6次和9次谐波。
3.2 平衡电抗器输入电流
根据基尔霍夫电压定律,平衡电抗器电流关系可表示如下。
输出正端平衡电抗器电流关系为
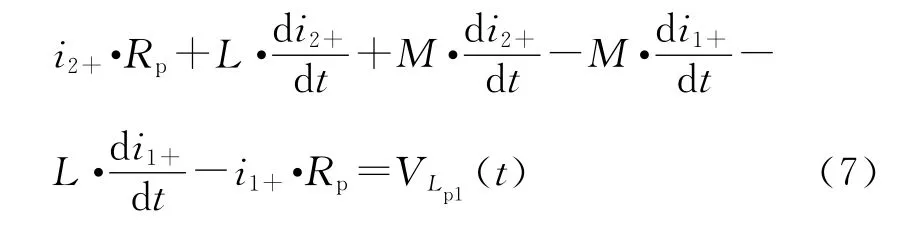
负端平衡电抗器电流关系为

正负输出端电抗器激磁电流为
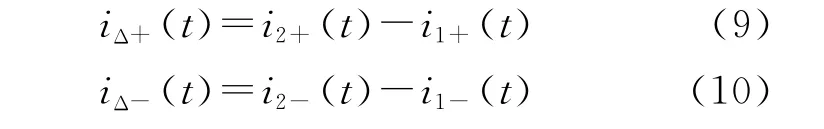
根据L=M的条件假设,式(7)、式(8)化简得:
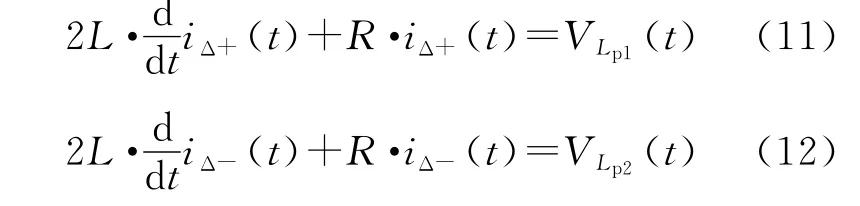
式中:iΔ+(t),iΔ-(t)为平衡电抗器的激磁电流。可以看出,该激磁电流和三相输入电压、平衡电抗器电感和内阻有关,解此微分方程,即可求出激磁电流的大小。
正输出端平衡电抗器激磁电流为
韶钢焙烧分厂、广西岑溪市和兴砂砖厂、广东省水电二局郴州莽山水库工程、韶关市东逸工贸有限公、湖北德耀建设工程有限公司承建的贵州凯里碎石制砂生产线,对比本工艺流程,选用本公司的专利产品,升级更新了部分工艺环节,对提高生产效率、提高成品砂连续级配等质量、节省用电、减少维修、降低生产成本,都产生明显的效果。

负输出端平衡电抗器激磁电流为

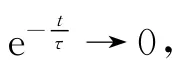
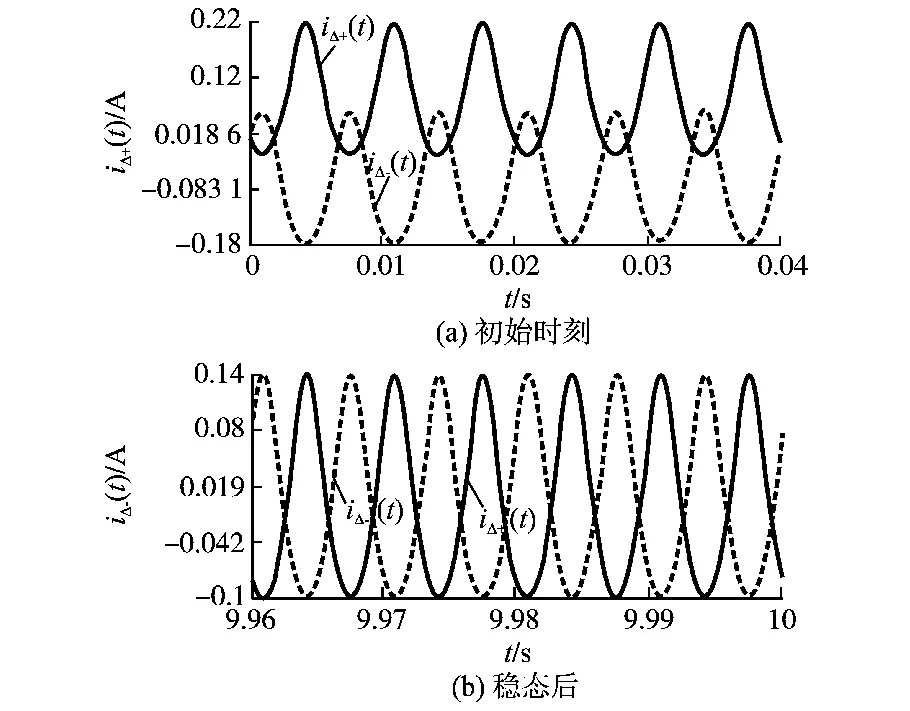
图3 平衡电抗器激磁电流曲线图Fig.3 Magnetizing current curves of interphase reactor
可以验证稳态时刻激磁电流的峰值和Rp的大小没有关系,且从稳态电流来看,正负输出端平衡电抗器激磁电流的峰值基本一致,因此,只需计算正输出端平衡电抗器的临界参数。根据式(13)可求出稳态条件下激磁电流的峰值为
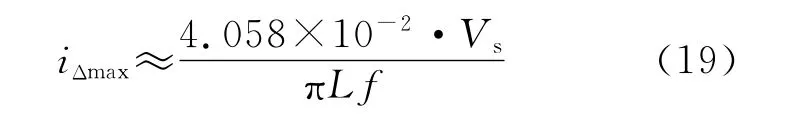
从式(19)可以看出,平衡电抗器激磁电流和三相输入电压、频率和平衡电抗器的电感量有关,从公式推导可看出,电抗器激磁电流的形成是电路本身固有的特性,因此激磁电流只能减小,但不能消除。
3.3 平衡电抗器临界参数的选取
由于前级移相变压器存在激磁电流,因而对于每个芯柱的磁势平衡方程将为
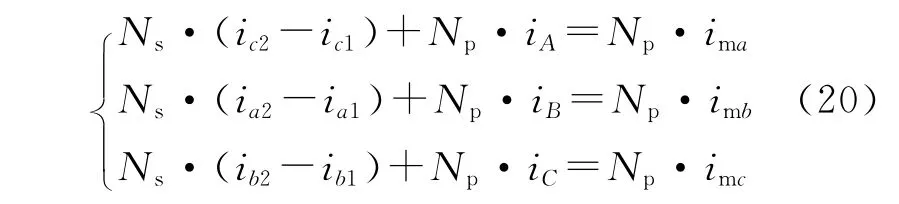
其中,imx为移相变压器激磁电流,其相位与各芯柱输入相电压的相位一致。以A相为例,由于长绕组Np中叠加了激磁电流,将导致电流ia2有效值大于ia1电流有效值,反映到直流输出侧,则滞后绕组侧整流桥的输出电流大于超前绕组侧整流桥的输出电流,这将会使平衡电抗器出现直流磁势,因此在计算平衡电抗器电感量时,需要考虑移相变压器激磁电流的影响。为了简化计算,移相变压器激磁电流对平衡电抗器激磁电流的影响按照最大值确定。
设平衡电抗器激磁电流峰值iΔtmax,移相变压器空载相电流峰值iAm,则理想状态下平衡电抗器激磁电流的峰值为
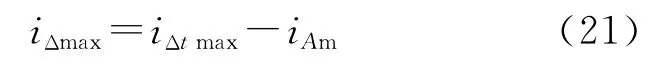
从式(19)可得出临界电感的计算公式为
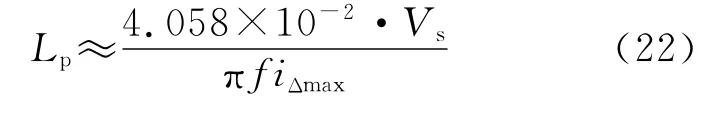
式中,Lp为平衡电抗器单个绕组临界电感,为了保证足够的电感量,常采用铁芯式结构,并且磁路中不加气隙,在设计平衡电抗器时,既要满足电感量的要求,也要充分考虑电抗器饱和的因素,即满足如下关系:
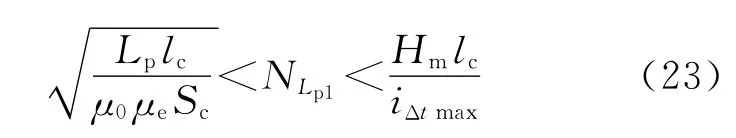
式中:lc为磁路平均长度;μe为有效磁导率;μ0为真空磁导率;Sc为铁芯有效截面积。Hm的取值根据铁芯磁化特性而定,如图4所示,其中μi为初始磁导率。
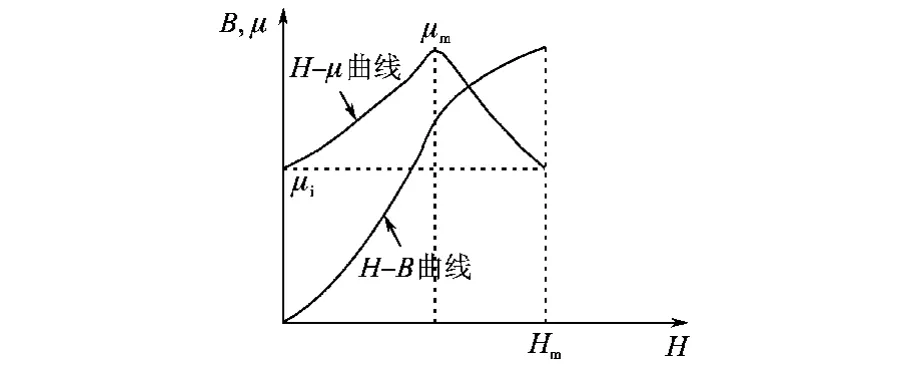
图4 铁芯磁化特性曲线Fig.4 Core magnetization curves
由式(23),可得,
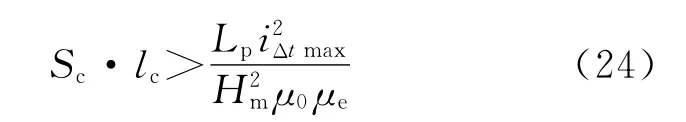
根据式(22)、式(24)可得出在iΔtmax=2iAm时,可使式(24)不等式右侧取值最小,进而可使Sc·lc取值达到最小,但iΔtmax取值过小,电感量会增加,电抗器的体积和重量会增加,损耗也会增加,因此若电抗器的基本参数已定,则在满足式(24)前提下,iΔtmax可适当增加,原则上不超过额定负载电流的10%[11]。确定了iΔtmax,Sc和lc后,便可计算出线圈的匝数,并进行结构计算。
4 仿真验证及实验
为了证明理论分析的正确性,利用Saber仿真软件对电路进行仿真分析。其中,Vin=220V,iAm=0.12A,负载采用阻性负载,其阻值RL=87 Ω,平衡电抗器单绕组电感L=420mH,移相变压器匝数为Ns=138匝,Np=760匝,短绕组漏感Lσ=200μH。
图5给出了在考虑移相变压器激磁后的绕组电流波形和激磁磁势曲线。从图5可以看出ia2有效值大于ia1有效值,移相变压器输出电流ia′有效值大于ia″有效值,即滞后绕组整流输出电流大于超前绕组整流输出电流。
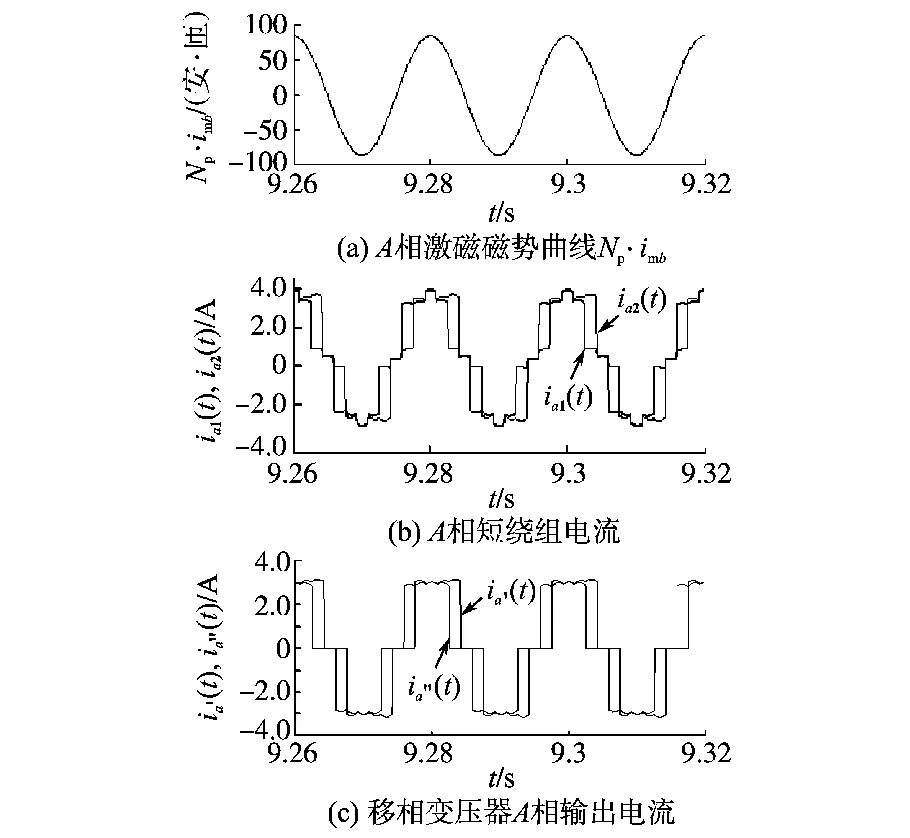
图5 移相变压器A相短绕组电流及磁势图Fig.5 A-phase winding current and magnetic potential of autotransformer
经式(19)计算得iΔmax=0.144A,仿真波形如图6所示,其中图6a为不考虑移相变压器激磁电流和漏感时的仿真波形;图6b为考虑移相变压器激磁电流时的仿真波形;图6c为考虑移相变压器激磁电流和漏感的仿真波形。从仿真波形可看出,在不考虑漏感的影响下,理论计算与仿真结果是吻合的,但漏感的存在会使均流效果更为理想。
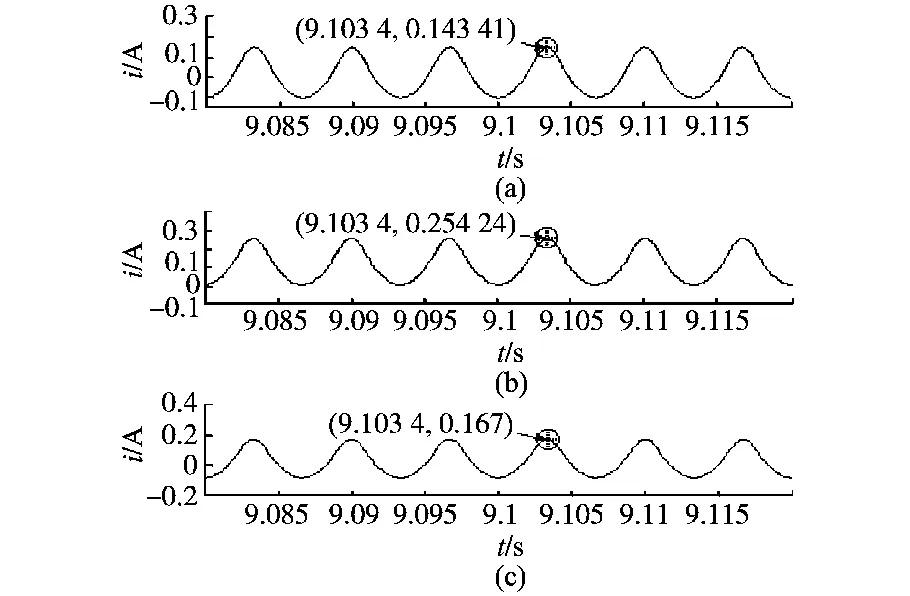
图6 电抗器激磁电流仿真波形Fig.6 Simulation waveforms of interphase reactor magnetizing current
实际情况下,平衡电抗器铁芯是非线性的,因此需要防止电抗器饱和,尤其是在大功率整流中更应避免,所以平衡电抗器结构参数应满足式(24)的要求。图7给出了电抗器饱和时的仿真波形,饱和后输出电压和输入电流出现畸变,若二极管电流定额较低,则会造成二极管损坏。
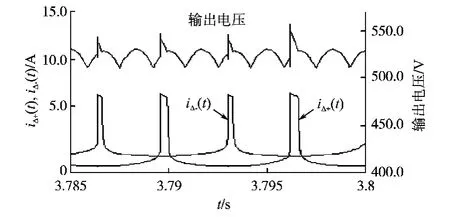
图7 电抗器饱和时仿真波形Fig.7 Simulation waveforms when interphase reactor is saturated
图8是实验波形。采用的实验参数如下:Vin=220V,RLoad=270Ω;平衡电抗器参数为:μe=1 985.53,Sc=7.36×10-4m2,lc=0.224m。图8a是平衡电抗器单绕组匝数为NL=226,实际电感量L=420mH的电抗器激磁电流波形。图8b是电抗器匝数为NL=207,实际电感量L=354mH的电抗器激磁电流波形。实际中由于移相变压器漏感的影响,激磁电流的实测值小于理论计算值。图8c是输入a相电流波形。图8d给出了平衡电抗器饱和时的激磁电流和输出电压波形,此时电抗器单个绕组匝数NL=156,实际电感量L=200mH。由图8d可见,电抗器饱和时,激磁电流峰值急剧增大至负载电流,说明此时负载电流只由滞后移相绕组整流桥提供,另一桥臂输出截止。此时,输出电压和输入电流出现畸变。
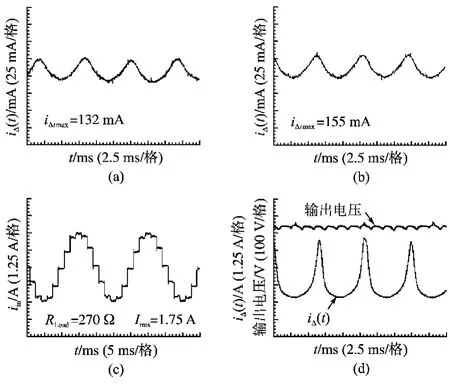
图8 实验波形Fig.8 Experimental waveforms
5 结论
通过对自耦式12脉波整流系统平衡电抗器等效电路的详细分析,在考虑了移相变压器激磁电流的影响情况下,结合平衡电抗器的工作特性,提出了一种简单有效的平衡电抗器临界电感的计算方法,给出了基本参数选取的范围,使平衡电抗器电感、结构参数的选取更为合理。通过仿真和实验,证明该方法计算的临界电感值具有足够准确性,能够满足工程需要,为自耦式12脉波整流系统平衡电抗器的合理设计提供了理论依据。
[1] Derek A Paice.Power Electronic Converter Harmonics Multipulse Methods for Clean Power[M].New York:IEEE Press,1996.
[2] Sewan Choi,Prasad N Enjeti,Ira J Pitel.Autotransformer Configurations to Enhance Utility Power Quality of High Power AC/DC Rectifier Systems[C]∥Particle Accelerator Conference,1995(3):1985-1987.
[3] 马义林,陈宇,任志新,等.新型12脉冲自耦变压整流器的研究[J].电力电子技术,2008,42(9):39-41.
[4] Liang Tsorng-Juu,Chen Jiann-Fuh,Chu Ching-Lung,etal.Analysis of 12Pulse Phase Control AC/DC Converter[C]∥Proceedings of Third IEEE International Conference on Power Electronics and Drive Systems PEDS,1999(2):779-783.
[5] 任志新.多脉冲自耦变压整流器(ATRU)的研究[D].南京:南京航空航天大学,2008.
[6] Dudi A Rendusara,Annette von Jouanne,Prasad N Enjeti,etal.Design Considerations for 12-Pulse Diode Rectifier Systems Operating under Voltage Unbalance and Pre-Existing Voltage Distortion with Some Corrective Measures[J].IEEE Transactions on Industry Application,1996,11(6):1293-1303.
[7] Cross A M,Forsyth A J,Cooper B.Modeling,Simulation and Validation of a Twelve-pulse Autotransformer Rectifier for Aerospace Applications[C]∥Power Electronics,Machines and Drives,2004.(PEMD2004).Second International Conference on(Conf.Publ.No.498),2004(2):528-533.
[8] Sewan Choi,Prasad N Enjeti,Ira J Pitel.Polyphase Transformer Arrangements with Reduced kV·A Capacities for Harmonic Current Reduction in Rectifier-type Utility Interface[J].IEEE Transactions on Power Electronics,1996,11(5):680-690.
[9] 崔立君.特种变压器理论与设计[M].北京:科学技术文献出版社,1995.
[10]马义林.自耦式12脉冲整流电路的研究[D].南京:南京航空航天大学,2009.
[11]陈亚宁.交流平衡电抗器的原理与设计[J].电子变压器技术,1995(1):18-21.
修改稿日期:2010-11-18
Determination of Interphase Reactor Critical Value in Autotransformer Based 12-pulse AC-DC Converter
MA Yan-lin,HE Li-gao,DU En-li,LI Xu
(CollegeofAutomationEngineering,NanjingUniversityofAeronauticsand Astronautics,Nanjing210016,Jiangsu,China)
In the autotransformer based 12-pulse AC-DC converter,interphase reactor is a key component of overall system.A detailed theoretical analysis of the equivalent circuit of interphase reactor was provided,so the relation between interphase reactor inductance and other circuit parameters was proposed.In considering the influence of autotransformer magnetizing current to interphase reactor magnetizing current,a simple and effective method was presented to calculate the critical value of the reactor.Simulation and experimental results verify the validity of the calculation approach.The calculated critical value is accurate enough to meet the engineering need.The size of interphase reactor can be further reduced.
interphase reactor;auto-phase-shift transformer;multi-pulse rectifier;critical inductance
TM461
A
马彦林(1982-),男,硕士研究生,工程师,Email:myl@nuaa.edu.cn
2010-05-09

