一种光伏发电系统变步长MPPT控制策略研究

刘栋，杨苹，黄锦成

（华南理工大学 电力学院 广东省绿色能源技术重点实验室，广东 广州 510640）

一种光伏发电系统变步长MPPT控制策略研究

刘栋，杨苹，黄锦成

（华南理工大学 电力学院 广东省绿色能源技术重点实验室，广东 广州 510640）

为了提高光伏器件的发电效率，提出一种变扰动步长的最大功率点跟踪算法，根据光伏组件输出P-U特性曲线上各点斜率的绝对值确定最大功率点跟踪的扰动步长，使搜索的快速性和稳定性同时增强。Matlab仿真验证结果表明：该算法能够实时对光伏组件输出功率进行跟踪调节，大大提高光伏系统跟踪最大输出功率速度的同时，有效降低系统输出功率在最大功率点处的振荡现象，减小光伏组件的能量损耗。系统实现简单，易于推广应用。

光伏发电；最大功率点跟踪；变步长

1 引言

在当今能源日益紧张的大环境下，太阳能作为一种巨大的“清洁能源”日益受到广泛的关注。随着光伏发电的快速推广应用，如何充分有效利用光伏组件、降低太阳能光伏系统的使用成本成为人们关注的焦点。其中，光伏发电系统的最大功率点跟踪（MPPT）［1］控制方法是提高光伏组件效率的有效途径。MPPT控制方法主要有扰动观察法、电导增量法等［2］。这些方法利用固定的扰动步长搜索光伏发电系统的最大输出功率点，不能同时满足搜索的稳定性和快速性要求；而使用模糊控制变步长的方法虽然有较好的效果，但模糊控制器的设计和参数的整定比较复杂，增加了设计难度和系统成本，不利于大范围推广使用［3-4］。

本文提出了一种实现简单的变步长扰动观测法，根据光伏组件输出P-U特性曲线上各点斜率的绝对值确定最大功率点跟踪的扰动步长，同时提高搜索的快速性和稳定性。通过Matlab进行仿真验证试验，并与定步长扰动观察法相比，仿真验证试验表明：所提出的算法对光伏组件功率变化的跟踪更具实时性，不仅能够提高系统快速跟踪日照变化的能力，而且可以有效降低输出功率在最大功率点处的振荡现象，提高对光伏组件的利用效率。

2 光伏发电系统MPPT的基本原理

要对光伏发电系统实施最大功率输出跟踪控制，首先需要建立光伏发电系统的数学模型，在此基础上，寻求合适的最大功率输出跟踪控制算法。

2.1 光伏电池的等效模型及输出特性

既考虑并联电阻，又考虑串联电阻的单个光伏电池的精确等值电路见图1。

图1 单个光伏电池的精确等值电路Fig.1 The exact equivalent circuit of single photovoltaic cell

单个光伏电池的输出特性方程为

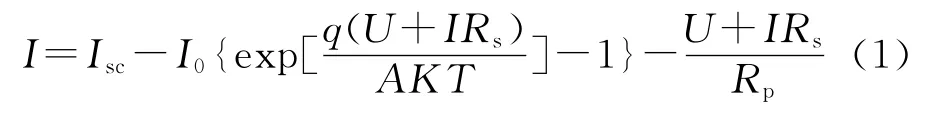
式中：Rs为光伏电池的内阻；Rp为光伏电池的并联电阻；I0为流过二极管的反向饱和漏电流；q为电荷量1.6×10-19C；K为 Boltzmann常数，值为1.38×10-23J／K；T为光伏阵列的工作温度，K；A为二极管的理想常数，其值在1～2之间变化［5］。

一般来说，质量好的硅晶片1cm2的Rs约在7.7～15.3mΩ之间，Rp在200～300Ω之间。一个理想的光伏电池，其等效串联电阻Rs很小，而等效并联电阻Rp很大，在一般的工程应用中，它们都可以忽略不计。

光伏组件输出功率P与输出电压U、电流I呈非线性关系，在不同环境即温度、日照强度下，光伏器件存在不同且唯一的最大输出功率点。光伏组件在不同的光照强度下的输出特性曲线见图2。

图2 不同的光照强度下的输出特性曲线Fig.2 The output curves under different light intensity

2.2 MPPT的定步长扰动观测法

针对光伏发电系统的特性，一般采用定步长扰动观察法实施最大功率输出跟踪控制。定步长扰动观察法的基本原理是：每隔一定的时间通过按固定步长改变占空比来增加或减少电压，并观测其后的功率变化方向，决定下一步的控制信号，通过多次这样的调节，使光伏组件最终达到最大功率输出。

定步长扰动观察法的控制流程图见图3［6］。

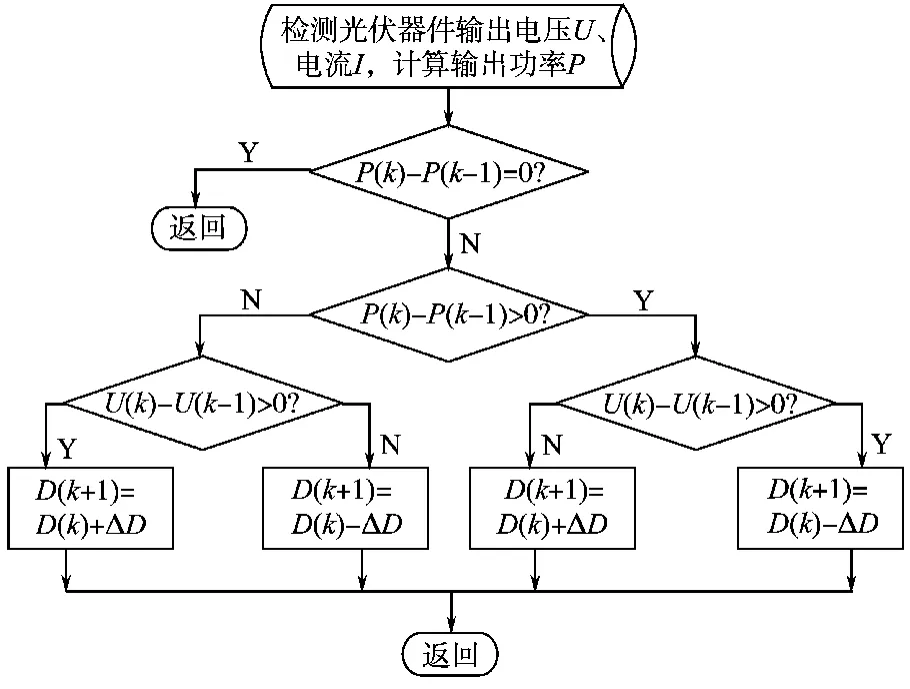
图3 定步长扰动观察法的控制流程图Fig.3 The flow chart of perturbation and observation method with fixed step

图3中占空比的变化步长ΔD为固定值，由于占空比变化步长固定，使得搜索的快速性与稳定性相矛盾［7］。

3 MPPT的变步长扰动观测法

定步长扰动观测法可以通过变化固定步长进行调节，通过减小ΔD可以改善光伏组件在最大功率点附近的功率振荡现象，但较小的ΔD将降低对日照变化的响应速度；而通过增大ΔD能够提高MPPT的搜索速度，但较大的ΔD使得光伏组件在最大功率点附近的功率振荡现象增强。为了克服上述定步长扰动观测法的不足，提出一种实现简单的变步长扰动观测法。

由图2b所示光伏组件输出P-U特性曲线可以看出，远离最大功率点时，电压变化量ΔU对光伏组件的输出功率的影响较大；而在最大功率点附近时，电压变化量ΔU对光伏组件的输出功率的变化影响较小。即光伏组件输出P-U曲线上各点的斜率根据距离最大功率点位置变化而变化，对图2b中光照强度1kW／m2的输出特性曲线上的k1，k2，k3，k4点做切线，见图4。

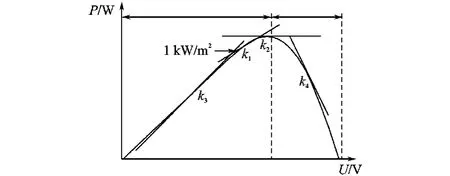
图4 光伏组件输出特性曲线的切线图Fig.4 The tangent map of output characteristic curve of PV module

由图4可得k1，k2，k3，k4点切线斜率的大小关系：

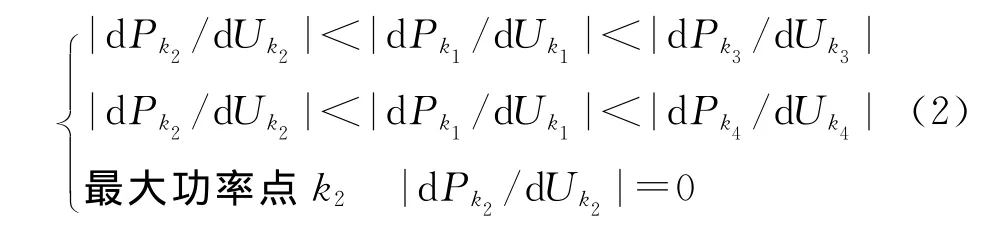
根据上述分析，可利用光伏组件输出P-U曲线上各点的斜率的绝对值确定扰动步长，来同时提高搜索的稳定性和快速性。

当采样周期很小时，输出电压变化量ΔU很小，则输出P-U特性曲线上各点斜率的绝对值等于光伏组件各点输出功率变化量与输出电压变化量的比值的绝对值，｜dP／dU｜＝｜ΔP／ΔU｜。即可以通过求得｜ΔP／ΔU｜，进而确定最大功率点跟踪的扰动步长。k时刻扰动步长ΔD（k）的计算方法为

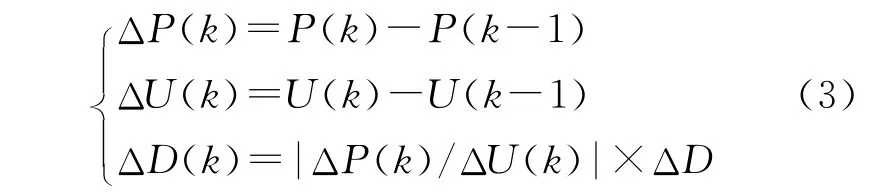
式中：ΔD（k）为k时刻的占空比变化步长；ΔP（k），ΔU（k）分别为k-1时刻到k时刻占空比变化引起的光伏模块输出功率变化量和电压变化量；ΔD为占空比的固定变化量，为定值。

变步长扰动观测法的控制流程图见图5。

图5 变步长扰动观测法的控制流程图Fig.5 The flow chart of perturbation and observation method with variable step

4 仿真分析

4.1 仿真原理图

利用Matlab中的Simulink软件环境得仿真电路图见图6。

图6 变步长扰动观测法仿真电路图Fig.6 The simulation circuit of variable step perturbation and observation method

其中MPPT算法的实现通过S函数进行编写。由于在实际系统中光伏组件输出P-U曲线不是平滑的，所以在仿真验证中为避免占空比的大干扰使得｜ΔP（k）／ΔU（k）｜取值过大从而降低算法稳 定 性，限 制｜ΔP（k）／ΔU（k）｜≤20。即 当｜ΔP（k）／ΔU（k）｜≥20时取｜ΔP（k）／ΔU（k）｜＝20。

4.2 仿真结果及分析

采用变步长的ode23tb（stiff-TR-BDF）进行仿真，设定初始条件为标准光照1kW／m2和常温25℃。仿真结果见图7。

图7 在固定光照和温度的仿真结果Fig.7 The simulation result of constant light intensity and temperature

从图7中可以看出变步长扰动观测法的暂态结束时间在0.04s，而定步长扰动观测法的暂态结束时间则是0.3s，变步长扰动观测法的搜索速度远远快于定步长扰动观测法，而且在接近稳态时的震荡现象较之定步长扰动观测法也较小。

设定初始条件为标准光照1kW／m2和常温25℃，在0.5s时光照变为800W／m2。仿真结果见图8。从图8中可以看出定步长扰动观测法可以根据光照强度的变化进行功率跟踪，而且跟踪速度快于定步长扰动观测法。

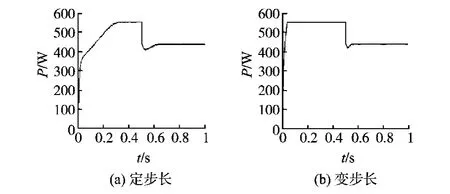
图8 在不同光照强度下的仿真结果Fig.8 The simulation results of different light intensity

5 结论

本文在对光伏模型进行分析的基础上，通过对MPPT算法的研究，提出了一种实现简单的变步长扰动观测法。利用Matlab进行了仿真验证，且在相同条件下与定步长扰动观测法相比较，验证结果表明该算法在各种日照变化情况下均能迅速稳定地重新输出最大功率，并有效地解决了定步长扰动观测法搜索的稳定性和快速性相矛盾的问题。

［1］ 赵争鸣，刘建政，孙晓瑛，等.太阳能光伏发电及其应用［M］.北京：科学出版社，2005.

［2］ Hohm D P，Roop M E.Comparative Study of Maximum Power Point Tracking Algorithms［J］.Progress in Photovoltaics：Research and Applications，2003，11（1）：47-62.

［3］ 任碧莹，钟彦儒，孙向东，等.基于模糊控制的最大功率点跟踪方法研究［J］.电力电子技术，2008，42（11）：47-48.

［4］ Simoes M G，Franceschetti N N，Friedhofer M.A Fuzzy Logic Based Photovoltaic Peak Power Tracking Control［C］∥IEEE International Symposium on Industrial Electronics，1998：300-305.

［5］ 周德佳，赵争鸣，吴理博，等.基于仿真模型的太阳能光伏电池阵列特性的分析［J］.清华大学学报：自然科学版，2007，47（7）：1109-1112，1117.

［6］ 张超，何湘宁，赵德安.光伏发电系统变步长MPPT控制策略研究［J］.电力电子技术，2009，43（10）：47-49.

［7］ 何薇薇，熊宇，杨金明，等.基于改进 MPPT算法的光伏发电最大功率跟踪系统［J］.电气传动，2009，39（6）：39-41.

修改稿日期：2010-11-15

Research on Variable Step MPPT Strategy for Photovoltaic System

LIU Dong，YANG Ping，HUANG Jin-cheng

（SchoolofElectricPower，SouthChinaUniversityofTechnology，GuangdongKeyLaboratory ofCleanEnergyTechnology，Guangzhou510640，Guangdong，China）

For improving the efficiency on power generation of photovoltaic（PV）device，a variable perturb step method was proposed which uses the absolute value ofP-Ucharacteristic curve′s points slope of PV device output to determine the variable perturb step and can enhance the search speed and stability at the same time.The Matlab simulation results show that this method can be effective to adjust PV output power in real time.It can greatly improve the tracking speed and reduce the oscillation around the maximum power point（MPP）to lower the engery lost of PV device.This system is simple and easy to promote and use.

photovoltaic power generation；maximum power point tracking；variable step

TM615

A

刘栋（1985-），男，硕士研究生，Email：657962482＠qq.com

2010-05-22