基于能量法的跨声速风扇叶片气弹稳定性研究

赵瑞勇，杨 慧，王延荣

（1.西安航天动力研究所，西安 710100；2.北京航空航天大学能源与动力工程学院，北京 100191）

0 引言

现代叶轮机械正朝着高性能和大容量方向发展，由流体诱发的叶片振动问题也越来越严重[1]。其中颤振就是1种典型的流体诱发自激振动[2]。严重的叶片颤振可能破坏发动机支撑结构，甚至导致整架飞机失事。因此，在发动机研制过程中，必须避免发动机在整个飞行包线范围内发生颤振[3]。各类叶片颤振都属于气动弹性稳定性问题。气动弹性试验破坏性极大，因此，通常应用计算机和CFD技术对气弹稳定性进行数值仿真研究。叶轮机自身十分复杂，采用直接流固耦合（FSI）计算分析耗时长，很难让人接受；目前，广泛采用能量法进行叶轮机械颤振研究，通过计算以转子振动的某一自然振型表现的颤振与流场之间的能量平衡来预测颤振。计算中通常忽略非定常气动力对振动模态的影响。因此，该方法实质上是不耦合，或精确地说是弱耦合的，也就不包括非定常气动力对振型和频率的反馈影响。基于能量法的简化方程之所以应用广泛，主要是因为作用于叶片的非定常气动力与力矩对金属叶片的振动模态与频率影响较小，可以独立进行结构动力学分析与非定常气动分析，极大简化了分析工作。在叶片气动弹性仿真计算中，由于结构变形，每一计算时间步都需要生成自适应计算网格。采用合理的网格更新方法[6]和寻求高效率、高精度的CSD/CFD数据交换方法是耦合技术应用的关键。

本文针对刚性叶片由于变形较小，发展了3维线性插值理论来进行CSD/CFD耦合界面数据交换。

1 叶片结构动力学方程

本文使用有限元法计算叶片的固有振动特性，未考虑叶片间的相互影响，假设每个叶片的振动频率都相同，模型不计机械阻尼的影响。叶片离心负载下振动的结构动力学控制方程为

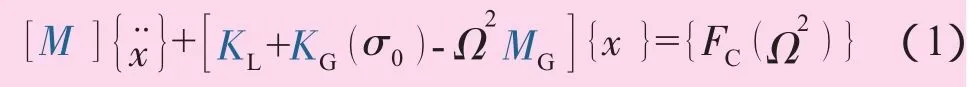
式中：[M]为单元质量矩阵；[KL]为单元弹性刚度矩阵；[KG]为单元离心刚度矩阵；（σ0）为离心力引起的初始应力向量；[MG]为单元离心质量矩阵；{x¨}、{x}分别为单元的加速度向量和位移向量；Ω为叶片的转动角速度；{FC（Ω2）}为单元节点平衡力向量，此处为离心分布的离散形式。

使用通用软件ANSYS来计算式（1）。在结构分析中，叶片固连在轮毂上，在叶根处为零线位移和零角位移约束，叶片其它位置为自由约束。给出叶片的各阶振型和固有频率，流场中叶片按照第i阶振型和固有频率进行谐振动

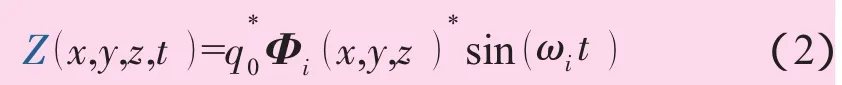
式中：Z（x,y,z,t ）为叶片表面各点的位移矢量；Φi（x,y,z）为叶片的第i阶振型矢量；q0为广义坐标振幅；ωi为第i阶振型的固有频率。

2 气动控制方程

假设叶片在做简谐振动的情况下引入运动网格，并对柱坐标系下的雷诺平均N－S方程进行求解来得到振动叶片所受到的非定常气动力以及气动力所做的功。

柱坐标系（φ，r，z ）下带有角速度为ω和有限体积表面运动速度Vg（ug,vg,wg）的3维积分型N－S方程为

式中：U为气动参数；E、F、G为无黏通量；Sl为源项。具体表达式见参考文献[7]。

湍流模型采用对分离模拟较好的SST模型[4],方程求解采用CFD软件FLUENT。

3 能量法-气动功

考察在1个振动周期内，流体与叶片发生能量交换，如果非定常气动力对叶片作正功，则叶片从气流中吸收能量，发生颤振[8]。

整个叶片的气动功为叶片单位面积上1个周期内气动功在叶片表面上的积分

定义等效模态气动阻尼[10]

式中：xcfd为叶片实际振幅；φ为模态振幅。

按照上述的能量法，当非定常气动力总功为正值时，模态气动阻尼为负，叶片振动发散。

4 CSD/CFD数据插值

由于气动计算网格比结构计算网格密，如图1、2所示，要进行气动与结构耦合计算，快捷、高质量的插值方法对计算时效和计算精度至关重要。本文改进了文献[9]中的3维线性插值算法，在程序中引入面积控制因子，减小了插值误差。该算法易懂，比复杂插值方法效率高。非常适用于非结构网格的计算。

图1 CSD网格

图2 CFD网格

该算法每个CFD格点选距离最近的10个FE网格点，引入面积控制因子选出其中不小于其值的最近的4个点，4个FE网格点每3个就可以组成1个平面三角形，求得每个平面三角形的单元中心，选定单元中心离CFD网格点最近的三角形平面作为插值平面△A1B1C1，如图3所示。

图3 FE网格点可选择插值面

每个CFD网格点沿选定平面法向量投影如图4所示。

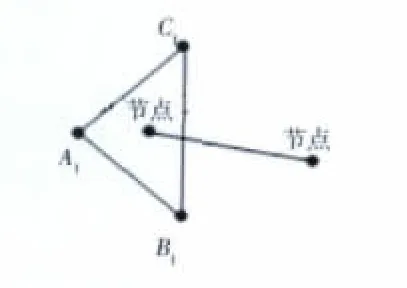
图4 CFD网格点投影到插值面

在点 A1、B1、C1上 分别作△A1B1C1的法线，使得 A1A2、B1B2、C1C2分别为点 A1、B1、C1的位移值。过点F做△A1B1C1的法线，在△A1B1C1和△A2B2C2上的交点分别为F1、F2，则F1F2为F点的位移值。如图5所示。

用Fortran编制插值程序，对NASA R67叶片前6阶模态进行了验证，都得到了很好的结果。以下仅以第1阶模态X方向的位移为例。插值前FE网格第1阶模态X方向位移如图6所示，插值后CFD网格模态位移等值线如图7所示。从图中可见，插值前、后数值一致。

图5 3维线性插值

图6 固体域FE网格第1阶X方向模态位移

图7 流体域CFD网格插值结果

5 动网格模型

在叶片气动弹性仿真计算中，叶片表面各节点每个时间步以某阶模态振型按固有模态频率做正弦运动，这样由于结构变形，每一计算时间步，周围流场需要生成自适应的计算网格。本文编制UDF程序用DEFINE_GRID_MOTION（）宏命令指定叶片表面各节点的运动形式，实现叶片的某阶模态振动。

由于计算模型单元数较多，非定常计算量大，为保证黏性计算精度和叶片表面附近网格随着叶片振动畸变小，采用弹簧光顺动网格模型，更新叶片周围流场网格。弹簧光顺网格模型更新过程如图8所示。

图8 弹簧光顺网格模型更新

6 算例与结果

6.1 NASA R67风扇叶片定常场计算与结果分析

本例计算模型选取1个扇区通道，对称面加周期边界条件，如图9所示。采用6面体非结构网格，共317833个节点，299509个单元；叶片表面10198个节点，10072个单元。不考虑叶尖间隙的影响，壁面设定为绝热条件。为了加速收敛，计算采用多重网格技术，V循环。在定常状态下，入口总压为1个标准大气压，风扇叶片转速按照设计转速给定，通过改变流量得到风扇性能曲线。试验得到的堵塞流量为34.96 kg/s，计算得到的堵塞流量为34.77 kg/s。不同流量下总压比计算值与试验值[12]的对比如图10所示，试验值和计算值分别按照各自的堵塞流量进行规一。从图中可见，二者吻合较好，但是总体上计算压比值比试验值稍低。近最高效率点下的计算值和设计值见表1。从表中可见，二者误差较小。

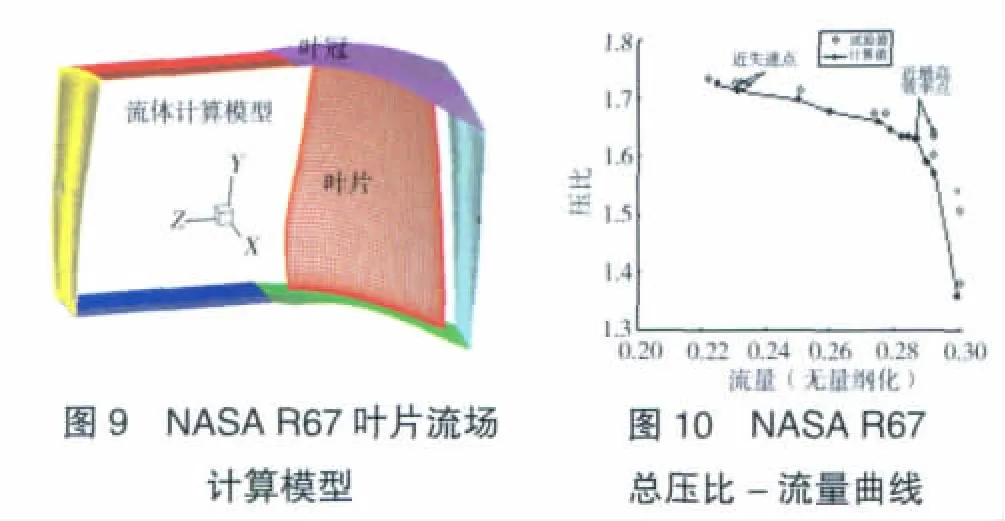
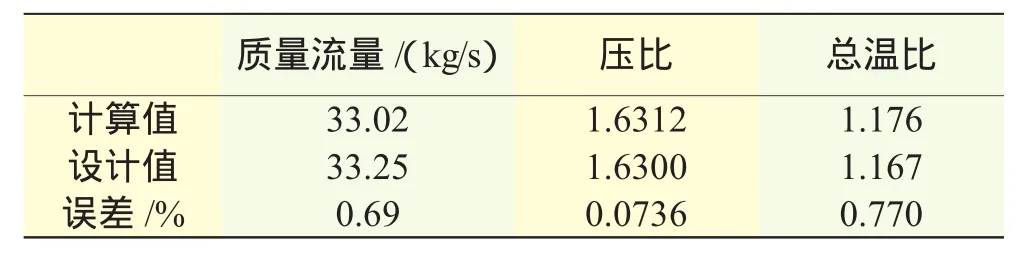
表1 NASA R67定常计算结果

近最高效率点90%叶高处马赫数如图11所示。从图中可见，90%叶高处叶片前缘斜激波和叶道中的垂直波呈“λ”形状，同时还可以观察到紧靠垂直激波后面有1道弱激波。

在设计转速下，叶片前缘压力值比后缘的低，吸力面上的激波波脚呈明显的λ形，如图12所示。

6.2 NASA R67叶片气弹稳定性计算与结果

6.2.1 NASAR67叶片有限元计算

叶片模型单元类型为solid45，X、Y、Z 3个方向共2×20×22个单元，共1449个节点。考虑离心力，转速为 16043r/min，泊松比 μ=0.3，弹性模 E=1.12E+11，选取钛合金材料密度ρ=4440 kg/m3。约束方式为叶根固支全约束，叶尖自由。叶片模态和频率如图13所示。

6.2.2 第1阶模态下叶片周期气动功分布

品牌农业区域效应逐步显现。卧龙区通过发展龙头企业、培育农业品牌等举措，充分发挥品牌农业企业的产业链优势，提高标准化、区域化、产业化经营水平，提高农业经济整体效益，有力地推进区域经济的增长。如石桥的月季，现已发展到卧龙区的各个乡镇；石桥的老姜历史悠久，姜质优良，在石桥的各个村都有不同规模的种植；谢庄龚河的玫瑰花、董营的红薯已发展到周边村种植；蒲山的桃、潦河坡的石榴、潦河的葡萄等因特色不同，形成了不同的旅游观光区，而且由于产品品质优良，在南阳乃至武汉、上海等大中城市备受欢迎，品质优良价位高，品牌效应有所显现。

本文计算了前3阶模态气动功分布，限于篇幅仅给出第1阶弯曲模态下耦合计算结果。

将有限元结果插值到如图2所示的CFD网格节点上，得到叶片表面位移数据，调用FLUENT动网格模型和UDF程序，并对模态位移进行归一化，指定流场中叶片实际最大振幅为1 mm进行叶片第1阶模态振动下的非定常计算。叶片前3阶模态振动下的总气动功和气动阻尼见表2。

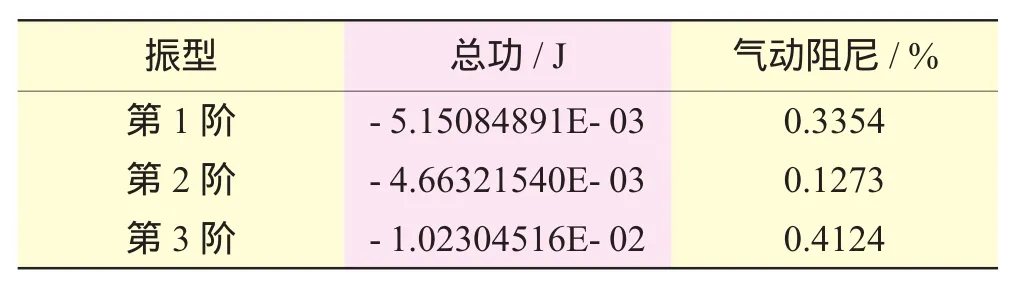
表2 前3阶模态气动功和气动阻尼比

根据能量法，由表2计算结果可知：前3阶模态振动非定常气动力对叶片作功为负，起到阻尼作用，系统能量耗散，叶片不会发生气弹失稳。当振幅为1 mm时,在第1阶模态（第1阶弯曲）和第3阶模态（第1阶扭转）下的气动阻尼较大，在第2阶模态（以弯为主的弯扭耦合振动）下的气动阻尼较小。

在第1阶模态下，叶片监视点位移与非定常气动力随时间变化如图14所示，由图14（b、c、d）中可见，非定常气动力较振荡叶片位移变化滞后一定相位角，该相位角是叶片表面非定常气动功变化因素之一。为了便于比较，放大了气动力幅值倍数。

叶片压力面和吸力面1个振动周期累积气动功分布如图15所示。在不同径向位置（10%、30%、50%、70%、90%叶高），气动功沿叶片弦向分布如图16～20所示。文中选取定常场计算70%和90%叶高处相对马赫数沿弦向分布作为激波参考位置，如图21、22所示。

对比图 15（a）、（b）可知，即使第1阶弯曲振动叶片表面总的气动功为负值，压力面和吸力面局部仍存在气动功为正值的区域（约70%～90%叶高，弦向0.6～0.9区域），对此应予以关注。

从图16、17中可见，在第1阶模态振动、50%叶高以下，由于激波的减弱或消失，压力面、吸力面气动功沿弦向受激波影响小，基本呈对称分布。

从图19、20中可见，在70%、90%叶高处，压力面、吸力面沿着弦向出现了绝对值较大的正功区。对比图19、21可知，在70%叶高激波位置处（约弦向0.35），气动功出现了波动；同样，对比图20、22可知，在90%叶高激波位置也出现了气动功的波动。

由此可见，在跨声速流动中激波的位置对叶片气弹稳定性有较大影响。

7 结论

（1）在前3阶模态振动下，非定常气动力对叶片作负功，气动阻尼为正值，叶片不会发生颤振。

（2）基于3维线性插值理论发展的CSD/CFD网格数据交换程序，可以实现流固耦合计算，该程序对网格限制性小，经对比发现插值结果误差小，从而减小了数据传递带来的结果误差。

（3）使用Fluent动网格模型对振荡叶片扰流进行了仿真计算，给出了叶片表面非定常周期气动功的分布情况，可为预测颤振提供依据。

（4）通过分析不同径向位置叶片沿弦线方向的气动功分布得出：激波位置和位移、气动力间相位角是影响非定常气动功分布的重要因素。

[1]袁新，金琰，畅国勇.叶轮机械中流体激振问题的流固耦合研究[C]//第八届全国空气弹性学术交流会论文集，北京：中国空气动力学会，2003：274-280.

[2]宋兆泓.叶片颤振[J].水利水电机械，2006（5）：45-52.

[3]蒋福庆.风扇-压气机亚、跨音失速颤振的发作机理及预测技术[J].航空发动机，1996（3）：9-15.

[4]张陈安，史爱明，刘锋，等.基于SST湍流模型的三维叶片气动弹性问题研究 [C]//第十届全国空气弹性学术交流会论文集，北京：中国力学学会，2007：345-351.

[5]王延荣,郝燕平,宋兆泓.涡轮机械叶片颤振及其研究进展[C]//中国航空学会第九届航空发动机结构强度振动学术交流会论文集，北京：中国航空学会，1998:265-271.

[6]徐敏，陈士橹.CFD/CSD耦合计算研究 [J].应用力学学报，2004，21（2）：33-36.

[7]胡运聪,周新海.振动叶栅非定常流动数值模拟与叶片颤振分析[D].西安:西北工业大学,2003.

[8]赵瑞勇,杨慧，王延荣.叶片颤振数值模拟方法研究[D].北京:北京航空航天大学,2010.

[9]张潇,王延荣.基于能量法的叶片颤振边界预测方法[D].北京:北京航空航天大学,2008.

[10]Moffatt S，Li He. Blade forced response prediction for industrial gas turbines,Part 1: methodologies[R].ASME 2003- GT- 38640.

[11]杨策,老大中,蒋滋康.风扇转子在设计转速下内部流场的数值研究[J].自然科学进展,1999,9（增刊1）：1312-1317.

[12]Anthony J S, Jerry R W, Michael D H，et al. Laser anemometer measurements in a transonic axial- flow fan rotor [R].NASA- TP- 1989- 2879.