网构软件信任机制的形式化研究

董宇欣，印桂生，谢新强，马志强

(哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001)

网构软件是一种新型软件形态，它具有自主适应性、协同性、反应性、在线演化性、多态性等形态特征，是传统软件在开放、动态、多变的网络环境下的延伸［1］.与传统软件形态不同，网构软件的出现使得Internet平台上存在着大量的可重复利用的构件资源.如何能够充分利用这些构件资源使其形成一个具有全面共享、自主协同的统一计算平台，从而解决大规模科学和工程计算问题［2］已成为网构软件技术面临的重要挑战之一.此外，由于网构软件系统的自组织特性，各类复杂系统中应用不同的信任管理机制，使得不同的应用系统中对信任的形式化定义和理解也存在着不一致性.例如，Lampson等［3］提出的访问控制演算逻辑以及BAN逻辑给出了安全认证协议的逻辑模型.Blaze等［4］提出了基于功能的静态概念信任模型PolicyMaker.Maurer等［5］提出的PKI信任模型［6］.信任是主体间的一种关系，目前还没有一个被广泛接受的严格定义［7］.对于信任的理解和定义大多局限于自然语言的描述，缺乏严密的数学模型及形式化方法对信任关系进行推导和量化.JØsang［8］认为信任是主体间的一种信念，信念表达了对信任实体行为和表现的期望，信任实体具有感性和理性之分，因此信念的背后必然存在着某种推理.本文基于信念逻辑给出信念公式和信任关系的形式化定义、分析、逻辑推理及证明过程，并给出了信任链建立以及多路径信任聚合的相关算法.

1 信念逻辑

假设信任关系模型采用五元组σ(ρ，α，η，κ，ν)表示，其中ρ表示构件主体集合，α表示假设的属性和不变量的集合，η表示主体的信念公式全集，信念强调的是主体根据自身知识和经验对外部环境的一种逻辑判断能力.κ表示主体ρ在α×η上的映射集合，表示主体的一个推理.ν是置信函数，ν(Qi，Qj)∈［0，1］，表示Qi对Qj的信任程度.φ表示命题符号，命题包含对信任主体的信任属性、权限、性能指标等特征的断言.逻辑连接词┐、∧、∨、⊃、∪、∩、→、|⇒优先级依次递减.|⇒表示信念关系推理符号.

定义1(信念公式)对于∀Q∈ρ，∀R⊆κ，如果主体Q在集合R上可以推导出一个真命题φ，则称存在信念公式(Q，R)|⇒φ.下面给出公式(Q，R)|⇒φ的如下递归定义:

1)如果φ是一个命题符号，则φ是原子公式.

2)如果φ是一个命题符号，则(Q，R)|⇒φ是一个信念公式.

3)如果η1、η2是信念公式，则逻辑运算η1∧η2，η1∨η2，η1→η2，┐η也是信念公式.

定理1 对于主体Q在条件R上的一条信任断言φi，如果(Q，R)|⇒φi成立，则必有φi∈κ成立，反之，如果φi∈κ，则(Q，R)|⇒φi成立.

证明:∵主体Q在条件R上存在信念φi，即(Q，R)|⇒φi成立，∴φi必然是Q的信念集合κ映射的一个子集.反之，当φi∈κ成立时，∵κ表示主体ρ×α×η上的一个映射子集，∴主体Q必然能够通过信念公式η推导出命题φi，显然定理1成立.证毕.

推理1 对于一个命题φi∈κ，(Q，R)|⇒φi与κ(Q，R)⊧φi相互等价，即主体Q在条件R上存在信念φi，当且仅当从相应的理论κ(Q，R)能够推导出命题φi，κ(Q，R)表示主体Q的一个理论.

由推理1，对于φi∈κ，φj∈κ，可以得出如下推理的等价关系:

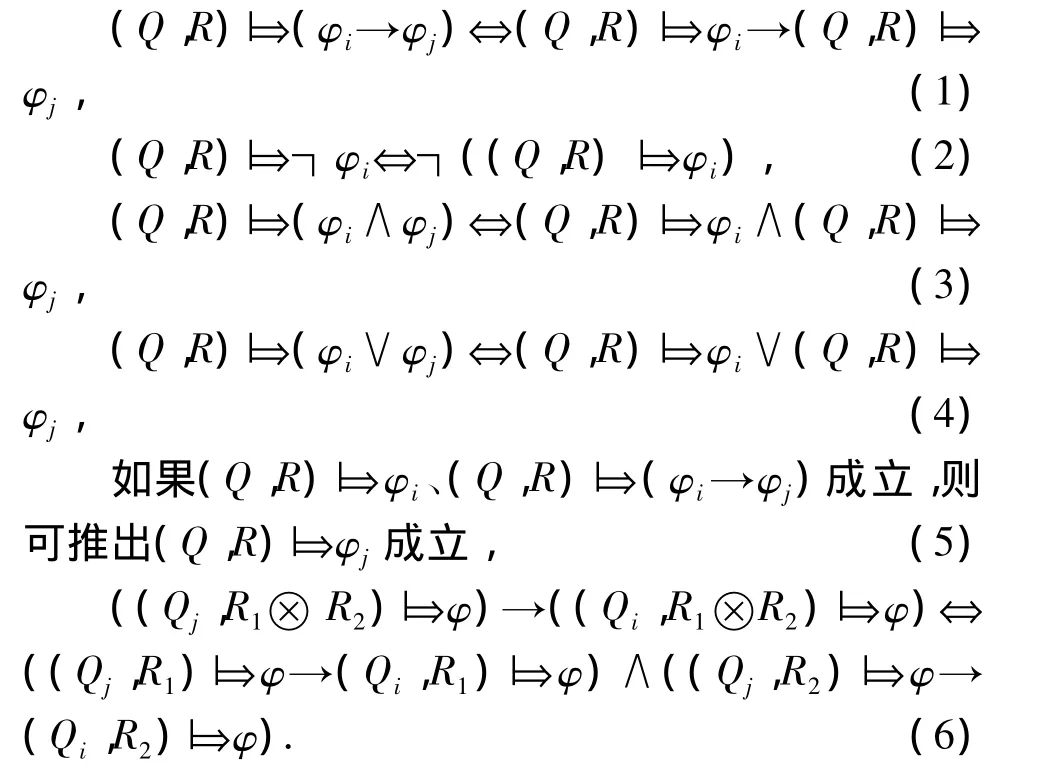
其中，⊗表示信念公式组合算子.

下面分别给出具体证明过程:

1)由推理1可知，(Q，R)|⇒φi⇔κ(Q，R)⊧φi，又∵(Q，R)|⇒(φi→φj)⇔κ(Q，R)⊧(φi→φj)，而κ(Q，R)⊧(φi→φj)⇔(κ(Q，R)⊧φi)→(κ(Q，R)⊧φj)⇔((Q，R)|⇒φi)→((Q，R)|⇒φj).证毕.

2)由推理1可知(Q，R)|⇒┐φi⇔κ(Q，R)⊧┐φi，而κ(Q，R)⊧┐φi⇔┐(κ(Q，R)⊧φi)⇔┐((Q，R)|⇒φi)，所以式(2)得证.

3)∵(Q，R)|⇒(φi∧φj)⇔κ(Q，R)⊧(φi∧φj)，κ(Q，R)⊧(φi∧φj)⇔(κ(Q，R)⊧φi)∧(κ(Q，R)⊧φj).又由推理1可得((κ(Q，R)⊧φi)∧(κ(Q，R)⊧φj)⇔((Q，R)|⇒φi)∧((Q，R)|⇒φj)，∴式(3)得证，同理式(4)、(5)、(6)可证.

2 信任关系形式化

根据ITU X.509对信任的自然语言描述为:“当主体A假设主体B将严格按照其所期望的那样行动时，则称A信任B”，也就是说对于主体B在条件R下推导出的命题，即信念ηi为真，则主体A在条件R下推导出的ηi也为真，即A对于B的断言是信任的，下面给出信任关系的形式化描述.

定义2 对于主体Qi在信念集合R上的一条断言φi，如果主体Qj在信念集合R上推导出的断言也是φi，则认为主体Qj在信念集合R上对φi的断言被主体Qi所信任，即如果(Qj，R)|⇒φi→(Qi，R) |⇒φi为真，则称主体Qi信任主体Qj，记作Qi(R，φ)≫Qj，其中≫表示信任关系推导符号.

信念强调的是主体的一种逻辑判断，是从主观上依据充分的证据得出的判断，不同的主体由于所处的环境、自身的条件差异，往往一个主体对事物的判断并不一定能被另一个主体所接受，因此信任链传递过程中必然存在着不同程度的损失.下面给出信任关系传播过程的形式化描述:

推理2 如果∃μ1⊆R，∃μ2⊆R，使得Qi(μ1，φ)≫Qj，并且Qi(μ2，φ)≫Qj同时成立，则可以推出Qi(μ1⊗μ2，φ)≫Qj，其中⊗为信念逻辑组合算子.推理2表明如果环境不变量对μ1、μ2同时成立，那么环境不变量对它们的组合也成立，μ1⊗μ2表示2个信任策略的组合，下面给出证明.

证明:由条件Qi(μ1，φ)≫Qj，并根据定义2得: (Qj，μ1)|⇒φ→(Qi，μ1)|⇒φ，同理由Qi(μ2，φ)≫Qj得:(Qj，μ2)|⇒φ→(Qi，μ2)|⇒φ，又由推理1的等价关系(6)可得:(Qj，μ1⊗μ2)|⇒φ→(Qi，μ1⊗μ2)|⇒φ，∴Qi(μ1⊗μ2，φ)≫Qj成立.证毕.

推理2提供了一个对复杂信任策略分解和进一步评估的途径，构件从外部获得的信任存在组合与分解关系，而信任评估所面对的对象大多是具有复杂结构的协议，不同的信任策略之间往往存在着多层次、多粒度的依赖和交互关系.

推理3 如果∃φ1⊆R，∃φ2⊆R，对于Qi、Qj、Qk，假设它们为不同的构件主体，如果存在Qi(μ，φ1)≫Qj，Qj(μ，φ2)≫Qk同时成立，则可以推出Qi(μ，φ1∧φ2)≫Qk成立.

证明:由条件Qi(μ，φ1)≫Qj，并根据定义2可知:对∀ε∈φ1，式(1):(Qj，μ)|⇒ε→(Qi，μ)|⇒ε成立，从而对于∀ε∈(φ1∧φ2)，亦满足公式1):(Qj，μ)|⇒ε→(Qi，μ)|⇒ε，同理，对于∀~ω∈φ2，(Qk，μ) |⇒~ω→(Qj，μ)|⇒~ω成立，则∀~ω(φ1∧φ2)，式(2): (Qk，μ)|⇒~ω→(Qj，μ)|⇒~ω显然成立.∴由式(1)、(2)可知，∃λ∈(~ω∧ε)⊂(φ1∧φ2)，使得(Qk，μ) |⇒λ→(Qi，μ)|⇒λ成立.又由定义2可知Qi(μ，λ)≫Qk成立，即Qi(μ，φ1∧φ2)≫Qk成立.证毕.

推理3细化了信任关系的分析粒度，给出了信任传递性成立的语义解释和约束条件.例如，A信任B是针对命题q，B信任C是针对命题p，显然不能认为A信任C.下面给出信任传递的进一步推导关系.

推理4 如果∀φ⊆κ，∀μ⊆R，对于公式Qi(μ，φ)≫Qj，Qj(μ，φ)≫Qk都成立，则Qi(μ，φ)≫Qk成立.推理4表明当Qi与Qj的信念公式集合μ及φ等价时，Qi对Qj的任何断言都认为是可信的，而Qi对Qk的信任则是通过Qj的直接推荐得到的.对推理4进一步推广可以得出信任链的定义.

推理5(信任链) 如果对于∀φ⊆κ，∀μ⊆R，Qi(μ，φ)≫Qi+1，Qi+1(μ，φ)≫Qi+2，…，Qn－1(μ，φ)≫Qn同时成立，则可以推导出Qi(μ，φ)≫Qn成立.

如图1所示序列Qi，Qi+1，…，Qn－1，Qn为从主体Qi到Qn的一条信任链，虚线显示了通过信任传递使得互不相连的主体间也能够建立信任关系.构件间信任关系的建立过程实际上也是信任链建立和传播的过程，2个构件节点之间往往存在着若干条信任链，如何选择一条置信度较高的信任链作为构件之间交互的通道显得尤为重要，因此本文3.3节给出了一种基于贪心策略的最优信任链计算方法的形式化描述.

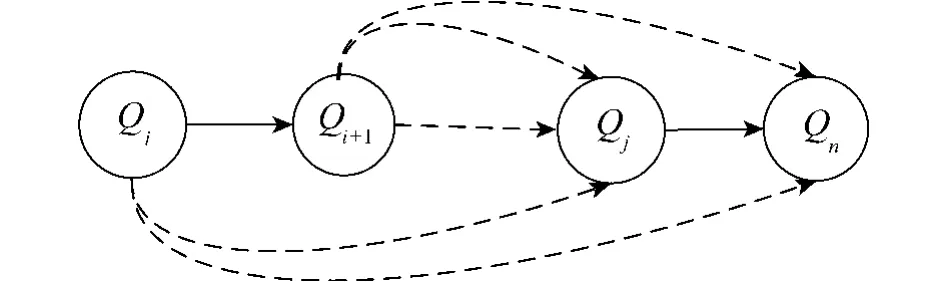
图1 信任链Fig.1 The trust chain

推理 6(信任聚合)如果∃φ1，∃φ2，∃φ3，∃φ4⊆κ，公式 Qi(μ，φ1)≫Qj，Qj(μ，φ2)≫Qk，Qi(μ，φ3)≫Qt，Qt(μ，φ4)≫Qk都成立，则可以得出Qi(μ，(φ1∧φ2)⊗(φ3∧φ4))≫Qk，其中⊗表示多路径信任聚合算子.

如图2所示，虚线描述了从Qi到Qk所有可以选择的路径.Qi与Qk间存在着多条可达的信任路径，通过多个路径的聚合来计算Qi与Qk之间的置信度，3.3节将进一步研究多路径聚合问题并给出了一种基于约束条件的多路径聚合算法.

图2 多路径信任聚合Fig.2 The multiple path trust aggregation

3 信任关系建立的形式化描述

本节通过信任关系的形式化定义对PKI［9］信任模型进行形式化描述和推演.

如图3所示为桥CA结构模型，采用BCA桥接方式互通3个不同的PKI域，即严格等级CA域、独立CA域和网状CA域，其中圆形为CA实体，箭头表示证书，双向箭头为交叉证书，长方形表示构件实体，桥BCA用三角形表示，虚线描述了其中的一条信任链传递过程.不同的信任域采用的信任策略不同，各种信任域之间通过BCA互通形成更大规模的信任域.假设＜G＞是信任网络的无负权有向图，且不存在环路，下面给出在PKI模型中信任关系建立的过程.

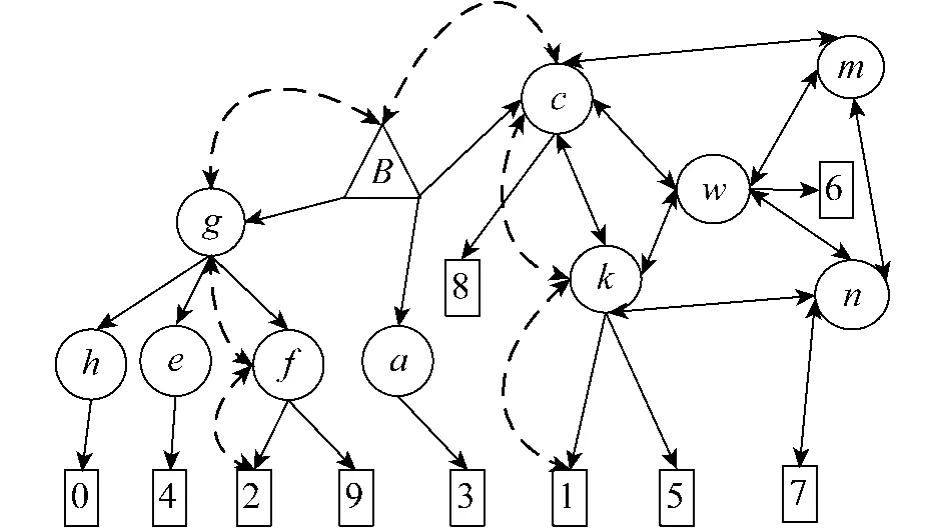
图3 BCA信任模型拓扑结构Fig.3 The topology structure for BCA trust model

3.1 信任链随机搜索算法RSTC的形式化与推演

构件节点间信任关系的建立过程也是信任链搜索和计算的过程.一种思路是通过考察G中所有可能的路径来确定是否存在从Qi到Qj的信任链，一条最长的路径就是＜G＞中长度最多为n的节点序列(假定不存在环路)，n是＜G＞中的节点数(如果从Qi到Qj存在有向路径，那么就存在长度不超过n的有向路径，因为路径上不需要重复节点)，但是这些路径数最坏情况下有nn条，即＜G＞中节点数的指数倍.显然，当构件集群规模足够大时，算法时间复杂度是NP类的.下面给出一种基于标记的随机搜索算法(random searching for trust chain，RSTC)的形式化描述如下:

1)对于输入＜G＞，Qi，Qj;

2)在节点Qi上做标记;

3)重复下面步骤4)～6)，直到不再有节点被标记;

4)扫描＜G＞的所有边.非确定性的选择一条边(a，b)，并且满足a被标记而b没有被标记，并转向5);

5)如果a使用公钥验证b的证书成立，则a的信任策略集合为ηQa=ηQa∪ηQb;

6)计算置信函数ν(a，b)，如果置信度ν(a，b)≥νmin，νmin为最小置信度阈值，那么标记b;

7)若Qj被标记，则接受;否则拒绝;

下面进一步分析算法的可行性，显然步骤1)、7)只执行1次，步骤4)、5)、6)最多执行n次，其中n为节点总数，用到的总步数是1+1+3n，所以时间复杂度为O(n)，因此RSTC属于P类问题.以图3构件Q1对Q2建立信任关系的过程为例，假定Q1随机选择的路径为图中虚线所示的路径，即 p1: Q1→Qk→Qc→QB→Qg→Qf→Q2.根据上述算法描述，对构件Q1与Q2信任机制的建立过程进行形式化推演.

根据定义2的形式化定义，对p1上相关构件主体的初始信任策略集合作如下形式化描述:

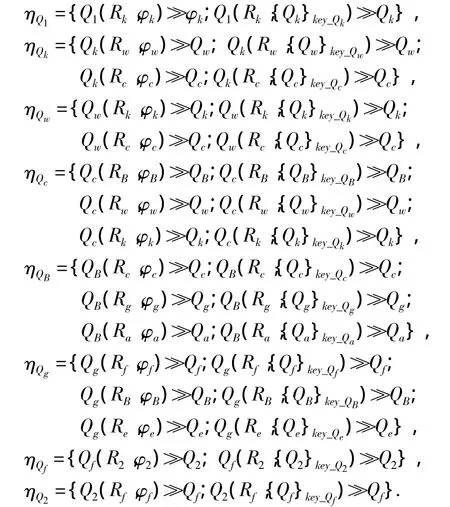
其中:{Qk}key_Qk表示构件主体Qk的密钥绑定为key _Qk，Q1(Rk，{Qk}key_Qk)≫Qk表示构件主体Q1信任Qk的密钥为key_Qk.路径上相关节点的数字证书语义表述为

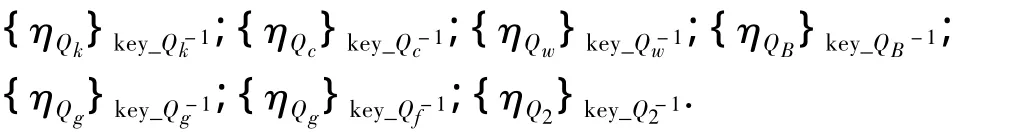
假设Rij=Ri⊗Rj，表示Qi与Qj不同信任策略及约束条件Ri、Rj的合成运算.Φij=φi∧φj表示Qi与Qj的信任断言φi、φj的合取运算.下面给出p1路径上信任关系建立的推演过程:

1)构件 Q1使用公钥 key_Qc验证证书{ηQc}key_Qc－1，如果验证成功，则计算置信度 ν(Q1， Qc)，如果(Q1，Qc)≥νmin则对Qc做标记，否则选择其他节点.Q1的信任策略集合为ηQ1=ηQ1∪ηQc.构件Q1根据Q1(Rkc，φkc)≫Qc;Qc(RB，φB)≫QB应用推理2、3可得Q1(RkcB，φkcB)≫QB;Q1(RkcB，{QB}key_QB)≫QB}.其中RkcB=Rkc⊗RB，φkcB=φkc∧φB.

2)构件Q1验证Q1(RkcB，{QB}key_QB)≫QB是否正确，如果QB的密钥在策略组合及约条件RkcB= Rkc⊗RB，φkcB=φkc∧φB下满足key_QB⊆RkcB则转向下一步验证，否则认证失败.

3)依次类推，经过图3虚线上各节点直到构件Q1根据Q1(RkcBgf，φkcBgf)≫Qf，Qf(R2，φ2)≫Q2应用推理2、3可得Q1(RkcBgf2，φkcBgf2)≫Q2;如果ν(Q1，Q2)≥νmin，则Q1与Q2成功建立起信任关系，并对Q2做标记，其中RkcBgf=RkcBg⊗Rf，φkcBgf=φkcBg∧φf.

4)判断Q2是否被标记，如果已被标记则接受;否则拒绝.

由于构件之间可能存在多条信任路径，信任关系的建立要考虑多条信任路径的综合情况，如图3所示，Qk与Qc存在着不同的信任路径Qk→Qc与Qk→QW→Qc，如果Qk对Qc不存在直接信任关系，而Qk信任Qw，Qw信任Qc显然不能说Qk不信任Qc.因此，3.2节将提出一种新的信任链搜索算法.

3.2 一种优化的信任链搜索算法的形式化

构件节点之间建立信任关系的过程也就是通过搜索网络节点寻找信任链的过程，2个构件之间可能存在多条信任链，某些时候构件节点只需要找到一条置信度最高的信任链作为交互的通道.现实信任关系网络中往往通过搜索一条具有较高置信度的最优信任链，通过该信任链上节点间的特殊关系和“连带”效应能够在一定程度上起到监督和限制节点，使其提供可靠服务减少恶意行为的作用.

基于上述分析并借鉴贪心策略在求解最优化问题的基本思想，提出一种基于贪心策略寻找最优信任链的算法(greedy strategy for trust chain，GSTC)算法，对GSTC形式化描述如下:

1)输入＜G＞，Qi，Qj:

2)初始化S={Qi};V={＜G＞中所有节点}; ν(Qi，Qt)={Qi初始时对 V中节点 Qt的置信度|t∈V－S};

3)若S≠V则重复4)～11)操作:

4)构件Qi使用公钥key_Qt验证与其相邻的各节点Qt的证书{ηQt}key_Qt－1，其中t∈V－S，并且Qt是Qi相邻节点;

5)如果验证成功则转向7)，否则转向6);

6)将验证失败的边Qi→Qt的置信度置为0，即ν(Qk，Qt)=0;

7)此时构件Qi的信任策略集合ηQi=ηQi∪ηQt;

8)求出与当前节点Qt相邻节点中置信度最大的边，即ν(Qt，Qk)=max{ν(Qt，Qx)|x∈V－S};

9)S=S∪{k};

10)对于每一个t∈V－S修改ν(Qi，Qt)=max {ν(Qi，Qt)，ν(Qi，Qk)⊗(Qk，Qt)}，其中⊗为信任聚合算子;

11)判断若S=V则算法结束并返回集合S，否则转向3);

12)如果Qj∈S，则接受，否则拒绝.

显然，上述算法的时间复杂度为O(n2)，因此属于P类问题.当算法成功结束时，集合S中存储的信任链就是从Qi到Qj的置信度最大的一条信任链，构件Qi依次经过集合S中的节点与构件Qj进行交互，由于每次交互时选择的都是最可靠的交互对象，从而有效降低了信任传播过程中的风险.对于信任链置信度的具体计算可以根据路径上节点的重要程度而分配不同的权重，而对于信任链过长的问题，我们也可以进一步修改上述算法，设置信任链最大跳数，限制由于信任链过长所带来的风险以及计算过于复杂等问题.此外，当存在多条信任链具有相同置信度时，我们应该从中选择一条抖动系数最小的.虽然上述算法是可行的，但是这种最优化信任链也存在着缺点，比如抗干扰能力差，评估带有片面性等.为此我们可以修改算法，找到k条信任链进行信任链聚合，其中k∈［1，2n］，当k取1时显然是GSTC算法的特例，当k=pathn时，是一种信任链聚合的综合评价方式，pathn是2个节点间所有可达的全路径数.一般取k=0.5pathn，因为通常情况下认为，当网络规模很大时，网络中恶意节点数不会超过网络规模的一半.

3.3 多路径信任聚合算法MPTA的形式化

单一信任链在一些情况下是可以用于评价构件节点信任状况的，而在一些对信任度要求很高的网络中，单一信任链难以满足这一要求，为此本节提出一种基于递归回溯思想［10］求解多路径信任聚合的受限问题的方法，并在多路径信任链搜索过程设置了显示约束条件，通过约束来限定信任链的某些属性，如通过限制信任链置信度的最小阈值和信任链的最大长度来减小动态解空间树的规模，同时这种显示约束也能够有效的减小信任链的“抖动”，限制单个节点波动过大的问题，以及由于信任链过长导致风险系数增加等.

求解多路径信任聚合算法的基本思路是:对于节点Qi与Qj，搜索从Qi到Qj满足约束条件的所有可达路径，并对这些路径进行分类，分别赋予相应的权重，通过加权求和的方法对节点Qj进行多路径聚合评价.设path［n］用于暂存遍历过程中的当前路径，visited［n］为节点访问标志，visited［i］=1表示节点Qi已被遍历过，visited［i］=0表示节点Qi未被遍历过.value用于存储节点Qi对Qj的多路径信任聚合值，初值为0，设置计数器count用于记录符合约束条件的信任链的条数，初值为0.下面给出多路径聚合算法MPTA(multiple path trust aggregation)的形式化描述如下:

MPTA(＜G＞，Qi，Qj，len):

1)初始化向量path［len］={Qi}，len记录当前信任链的长度，初始值为0，标记当前节点Qi即visited［Qi］=1;

2)如果已经找到一条信任链，即当前节Qi等于Qj，则执行以下3)～7)，否则转向8);

3)判断此信任链的长度，如果不大于最长信任链限定的阈值，则转向4)，否则，放弃此信任链;

4)判断此信任链的置信度 是否大于最低信任阈值，如果是，则转向5)，否则，放弃此信任链;

5)判断此信任链抖动因子是否小于最小阈值，如果是，则转向6)，否则，放弃该信任链;

6)根据此信任链上节点序列的重要程度或者权威性对此信任链的相关数据进行分类和挖掘，并赋予相应的权重μi，其中μi∈［0，1］，∑μi=1，i=1，2，3…n;

7)计算:value=value+μi*ν，count=count+1;

8)查找当前构件节点Qi的所有邻节点p，当visited［p］=0时递归执行MPTA(＜G＞，p，Qj，len+ 1);

9)将当前节点Qi的访问标志visited［Qi］置为0，path［len］置为0以便进入回溯过程;

算法执行结束返回从Qi到Qj满足约束条件的所有信任链的置信度之和value，取value的平均值即value/count作为多路径信任聚合的置信度.分析上述算法的时间复杂度，假设采用邻接表作为图＜G＞的存储结构，可知每次递归回溯的最大深度为O(e)，其中e为＜G＞弧数，e的最大值为n(n－1)/2，又由8)可知执行递归的可能邻节点为n个，其中n为＜G＞重节点总数，因此时间复杂度为O (n3).多路径信任聚合算法提出能够解决了当存在多条信任链时的聚合问题，这一算法同样可以用于求解多个节点对某一个节点的综合推荐问题，第4节将进一步通过实验给出多路径信任聚合算法的分析.

4 对GSTC和MPTA算法的实验分析

以图3的拓扑结构图为实验配置模型，模拟构件Q1与Q2建立信任关系的过程，对于图3中Q1搜索Q2的信任路径所经过的所有可能的弧有:(f，2)，(g，f)，(B，g)，(c，B)，(1，k)，(k，w)，(k，c)，(k，n)，(w，c)，(n，w)，(m，c)，(w，m)，(n，m).基于统计学理论可以认为网络中节点的信任状况是服从正态分布的，即服从N(μ，σ2)的分布，因此，采用正态随机数模拟上述所有弧的权值即节点间的置信度ν，实验基于C++平台分别实现了 RSTC算法、GSTC算法和MPTA算法，每次对所有弧的权值采用正态随机数赋值，分别输出单一信任链和多路径信任聚合情况下节点Q1到Q2的置信度.实验共模拟了100次，分别对 μ=0.95，σ2=0.005和 μ= 0.5，σ2=0.005两种情况进行了实验对比.

实验结果分析如下:如图4、5所示当μ=0.95，σ2=0.005，μ=0.5，σ2=0.005时，采用GSTC算法每次得到的置信度都是最大的，但从曲线的波动幅度不难看出GSTC算法抖动现象比RSTC算法的抖动现象明显.如图5所示，当网络信任状况较差时RSTC与GSTC曲线的波动幅度更大，这表明当网络信任状况较差时抖动会更加明显.RSTC每次得到的信任链的置信度相对于GSTC较低.此外，RSTC与GSTC曲线的整体抖动性都比MPTA较大，显然对于稳定性而言MPTA要优于RSTC和GSTC，这也是之所以采用MPTA信任聚合算法原因之一.虽然一次交互过程中选择最优信任链并不一定意味着受益一定是最大的，但是如果每次都选择一条最佳的信任路径，那么从概率上讲当交互次数n达到一定数量时，采用最优信任链获到可靠服务的机会要远大于采用随机搜索算法.

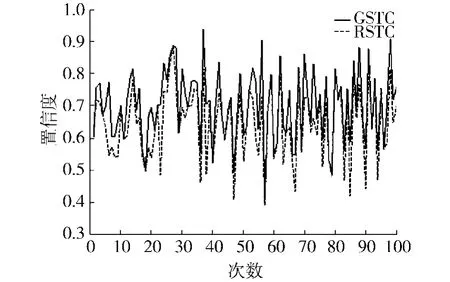
图4 当μ=0.95，σ2=0.005，n=100时的置信度Fig.4 Confidence curves when μ=0.95，σ2=0.005，n=100

如图6、7所示为μ=0.95和0.5，方差σ2= 0.005的情况，虚线为非约束条件下MPTA的置信度变化曲线，所谓非约束条件即是指不对信任链的长度、抖动系数、和最低置信度阈值加以限制.实线为约束条件下的MPTA的置信度变化曲线，假定限制信任链的长度不超过0.5n，其中n为网络构件节点总数，抖动系数最大为σ2.通过图6、7可以看出，多路径信任聚合过程中对于信任链的显示约束能够有效减少抖动现象，使网络整体信任状况趋于相对稳定，避免置信度较差的节点通过信任链传播到整个网络，能够有效控制恶意信任链的传播，同时减少了信任评估过程中的计算开销和网络负载.对于某些置信度较低的恶意信任链，如果不能及时的加以限制很可能导致对其他可信度较高的节点的评估出现较大偏差.

图5 当μ=0.5，σ2=0.005，n=100时的置信度Fig.5 Confidence curves when=0.5，σ2=0.005，n=100

图6 当μ=0.95，σ2=0.005，n=100时的置信度Fig.6 Confidence curves when μ=0.95，σ2=0.005，n=100

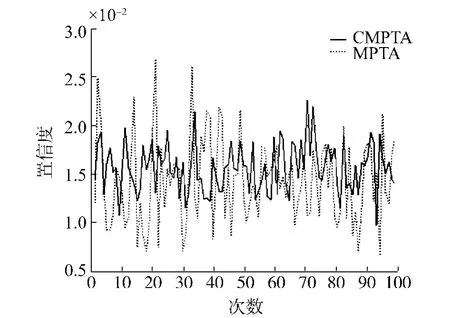
图7 当μ=0.5，σ2=0.005，n=100时的置信度Fig.7 Confidence curves when μ=0.5，σ2=0.005，n=100

5 结束语

由于构件集群环境是一个涉及多层次、多粒度、错综交织的动态环境，在这种环境中信任关系的定义、推理和建立过程是一个极其复杂的过程，本文基于信念逻辑，给出了信任关系的形式化描述，对信任关系的建立过程进行了推演，对于信任链、多路径信任聚合算法的提出有利于网构软件信任机制的进一步深入研究.目前，对于多路径、全路径信任聚合方法的研究不多，解决多路径、全路径信任聚合问题的关键是寻找一种时间复杂度较低的多路径搜索方法，本文尚有不足之处需要改进，比如对信任链上各节点的分析，对恶意节点的发现和预警、恶意信任链的传播缺乏有效的应对机制，此外，对于存在环路的信任链的信任传播过程中可能造成死锁的情况没有加以考虑.下一步工作将深入研究网构软件信任系统的形式化、自动化验证的方法，在此基础上开展信任策略自动评估工作.

［1］YANG F Q.Thinking on the development of software engineering technology［J］.Journal of Software，2005，16(1):1－7.

［2］袁禄来，曾国荪，王伟.基于Pi－演算的信任网络形式化建模［J］.系统仿真学报，2008，20(1):57－61.

YUAN Lulai，ZENG Guosun，WANG Wei.Formal modeling of trust networks using Pi－calculus［J］.Journal of System Simulation，2008，20(1):57－61.

［3］LAMPSON B，ABADI M，BURROWS M，WOBBERE.Authentication in distributed systems:theory and practice［J］.ACM Transactions on Computer Systems，1992，10(4):265－310.

［4］BLAZE M，FEIGENBAUM J，LACY J.Decentralized trust management［C］//Proceedings of the IEEE Symposium on Security and Privacy.Oakland，1996:164－173.

［5］LI N，MITCHELL J C，WINSBOROUGH W H.Design of a role－based trust management framework［C］//Proceedings of the 2002 IEEE Symposium on Security and Privacy.Berkeley，2002:114－130.

［6］MOSES T.Trust management in the public key infrastructure［EB/OL］.［2002－06－03］.http://www.entrust.corn/resources/pdf/trustmodels.pdf.

［7］GRANDISON T，SLOMAN M.A survey of trust inInternet applications［J］.IEEE Communications Surveys，2000，4 (4):2－16.

［8］JØSANG A.The right type of trust for distributed systems［C］//Proceedings of the 1996 Workshop on New security Paradigms.San Diego，USA，1996:119－131.

［9］SIPSER M.Introduction to the theory of computation［M］.Boston:PWS Publishing Company，2008:136－145.

［10］FOMIN F V，GRANDONI F.A measure＆conquer approach for the analysis of exact algorithms［J］.Journal of the ACM，2009:56(5):25－27.