利用开源CFD程序计算可压缩流场

郑群，李义进，孙兰昕

(哈尔滨工程大学 动力与能源学院，黑龙江 哈尔滨 150001)

计算机计算能力的迅速增长加速了CFD技术的发展，推进了CFD技术在工程实际中的应用.通过数值模拟，可以得到复杂流场的多种信息，从而为流场内部流动结构的深入研究提供了有力的手段.

可压缩全流场流动(如叶栅内流动)可以用密度方法或压力方法进行数值模拟.基于密度方法，求解马赫数较高的流动问题已取得了很大的成功，但对于马赫数很小的流动计算，此法受到诸多限制，可用预处理方法来解决［1-2］.基于压力方法求解流场问题，对马赫数的大小没有限制，即任何马赫数的流动均是适用的.

1 流体运动的控制方程组

绝对坐标系下的流体运动控制方程组在Favre平均(除了压力和密度本身以外，都用密度加权平均)下，得到如下形式的Navier-Stokes方程组:

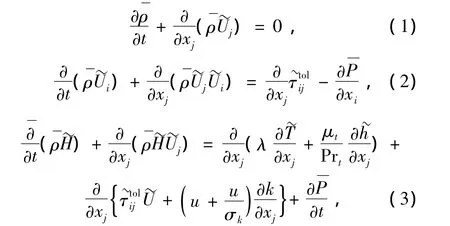
其中:

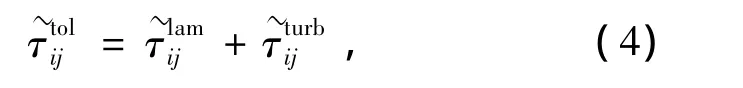
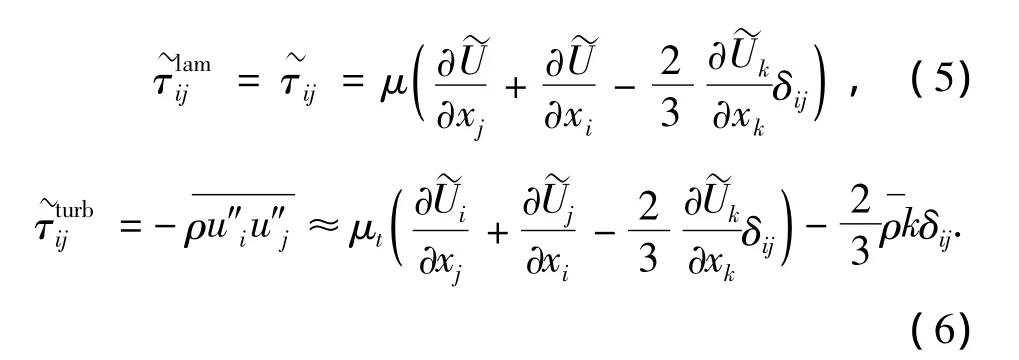
为了使上述流动方程组封闭，需要引入下面的几个补充方程.工质可看作完全气体，其状态方程为

式中:Cp为定比热常数.工质的分子粘性系数由萨瑟兰公式确定:

式中:T0=273.16 K，μ0为一个大气压下0℃时气体的动力粘性系数，Ts为萨瑟兰常数，与气体性质有关.

2 边界条件的处理

2.1 进出口条件

在可压缩流体计算中，进口为亚音速时，一般给定气体进口总压、总温，同时给定气体进口气流角.根据气体动力学理论，总压力与总温度的计算公式为

实施这一进口条件的简单方法为:每一步迭代用上一步(第一步用初始化的数据)的压力和气流角计算气流进口速度，再由总温的公式计算温度.

用k－ε模型计算湍流时，进口的k及ε值给定.没有具体的实验数据时，一般采用:

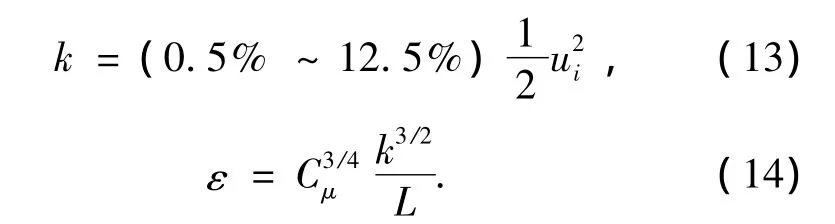
式中:L=0.07l，Cμ=0.09.

进口条件为超音速时，给定所有相关量.用kε模型来计算湍流时，进口k及ε值的给定与亚音速方法一样.

2.2 壁面条件

在标准k－ε模型中，采用壁面函数法处理湍流粘性系数.壁面临近节点P的湍流粘性系数计算如下:

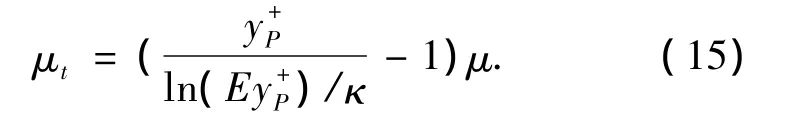
出口为亚音速时，一般给定气体出口的静压，其他量的梯度为零.出口为超音速时，所有量的梯度为零，即

其中:

kp按k方程计算.k方程壁面条件为方程壁面为

3 Navier-Stokes控制方程组的离散

OpenFOAM［5］运用张量方法和面向对象技术处理连续介质问题.只要能够将问题写成张量形式的偏微分方程，就可以根据OpenFOAM提供的基本程序写一个新的求解器［6-8］，从而求解此问题.在OpenFOAM中处理计算问题的流程如图1.

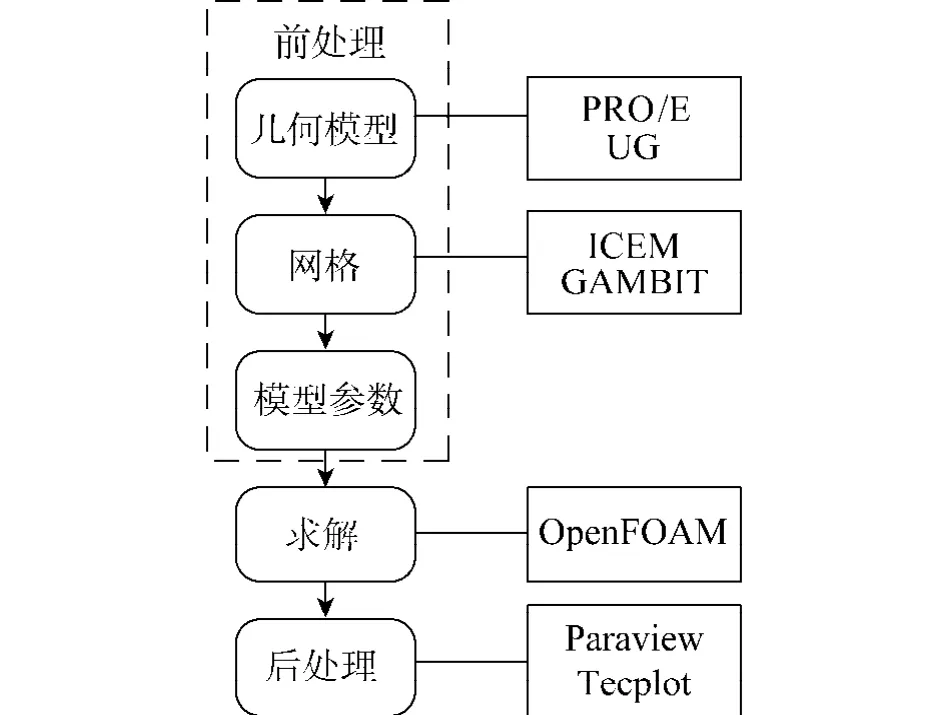
图1 OpenFOAM计算流程Fig.1 Calculation flow process of OpenFOAM

一个OpenFOAM求解例子一般包括constant、system和0文件夹.constant文件夹包括网格文件、物性参数和湍流参数等;system文件夹包括时间控制、离散格式和求解方法;0文件夹包括初始化参数和边界条件.计算结果存储在1000文件夹中(如图2).

在控制方程组的求解过程中，离散代数方程的求解耗时最多.OpenFOAM用Krylov子空间法(PCG和PBiCG等)和几何代数多重网格法(GAMG)进行加速求解.

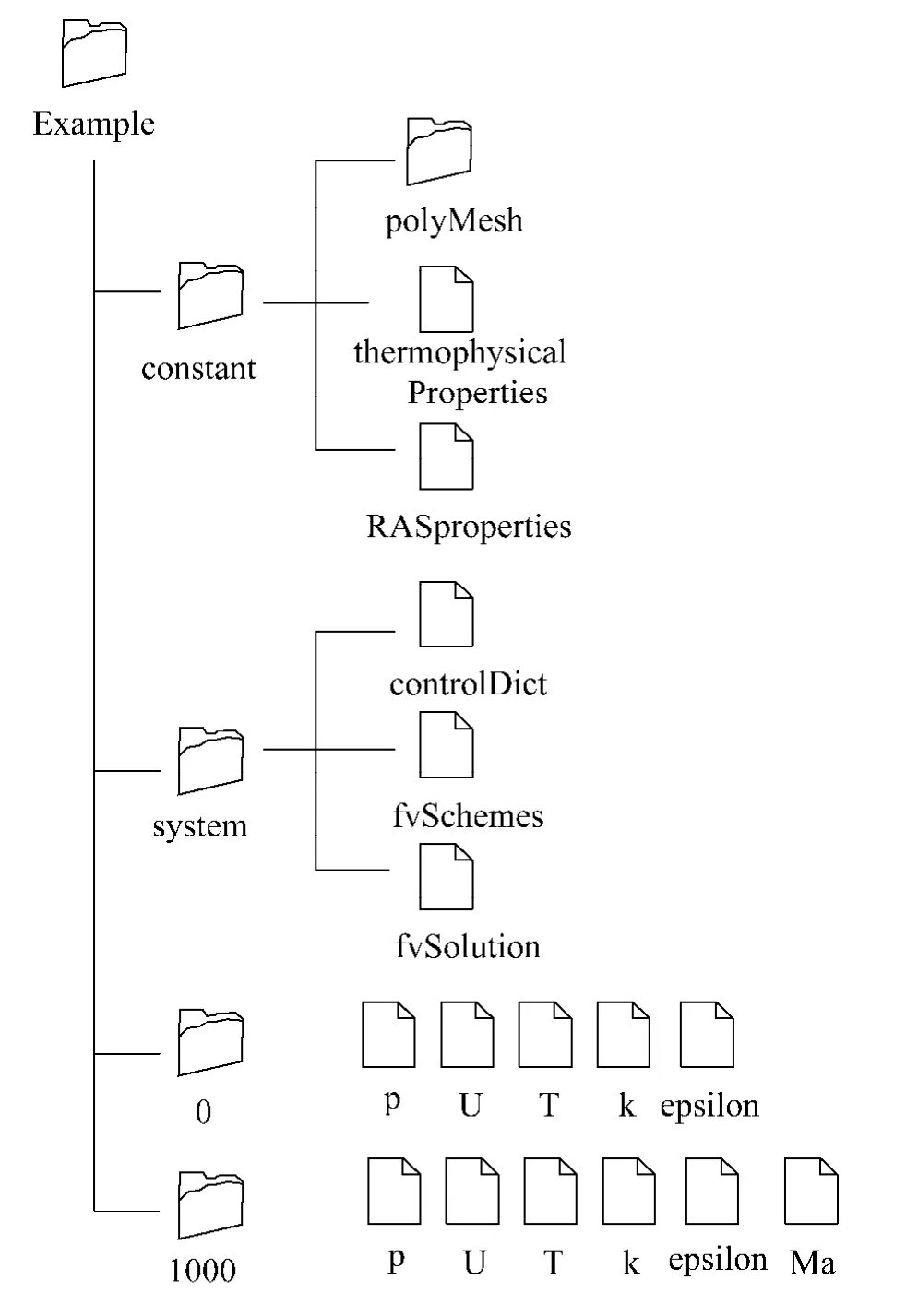
图2 OpenFOAM计算目录结构Fig.2 Calculation directory structure of OpenFOAM

Krylov子空间法是基于Krylov空间正交投影的参数依赖、非静态迭代方法，其思想是在Krylov子空间遍历搜寻解.即给一个线性系统Ax=b，这里A是一个大的、稀疏的n×n非奇异矩阵，根据标准的Richardson迭代，有

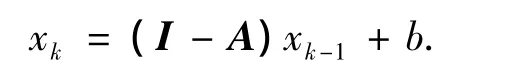
在变换的Krylov子空间上产生近似解:

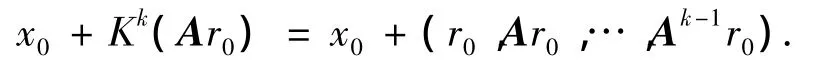
其中，对于给定初始矢量x0，有残量r0=b－Ax0.为了保证收敛性和健壮性，预处理技术是Krylov子空间法有效实施的关键组成部分.本文采用ILU(0)预处理技术，将Krylov子空间法中几种不同代数方程求解方法.

基于几何和分析的代数多重网格法(geometricalgebraic multi-grid solvers，GAMG)是加速线性代数方程迭代收敛的有效方法，这是目前国际上代数多重网格法研究领域中新发展起来的方法.其基本思想是在不同层次的网格上循环迭代，结合几何和代数2种途径来滤掉不同波长的误差分量，由于各种频率的误差分量都可以得到比较均匀的衰减，因而可以加快了迭代收敛速度.

3.1 TVD格式

Harten首次构造了二阶精度的TVD格式［9］，并且建立了一整套构造TVD格式的理论.TVD格式［10］如下:

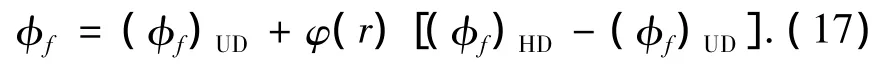
式中:(φf)UD为一阶的迎风格式，(φf)HD为高阶精度的格式，φ(r)是限制器，

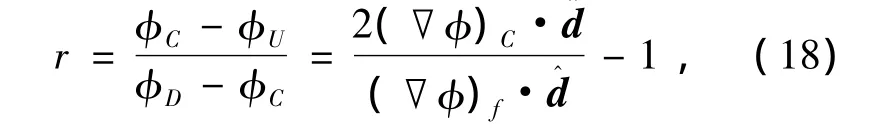
3.2 压力、速度和密度的耦合

3.2.1 离散动量方程

将动量方程中的压力梯度项独立出来，可得离散形式为

3.2.2 离散质量方程

质量方程对每个单元做积分，可得离散形式为

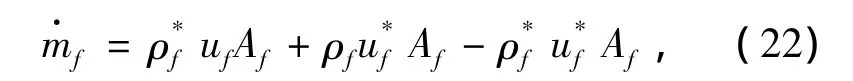
或

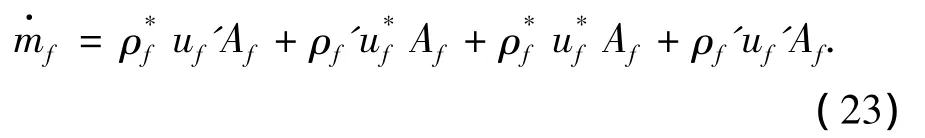
式中:“*”代表上一步的计算值，式(23)中右端第4项可忽略不计.

在可压缩流中，压力通过动量方程影响速度，通过状态方程影响密度，从而影响质量守恒，因此计算可压缩流场时，需要耦合压力、速度和密度.

3.2.3 压力方程

由状态方程(7)得

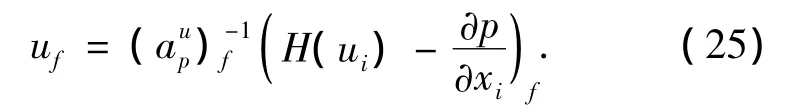
将式(24)、(25)代入式(22)，得面通量:将式(20)中的各项插值到单元界面上:

最终可得压力方程如下:

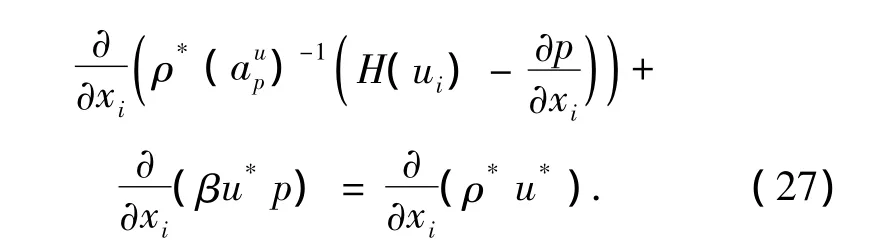
3.2.4 压力修正方程

压力修正量影响密度和速度的修正量:

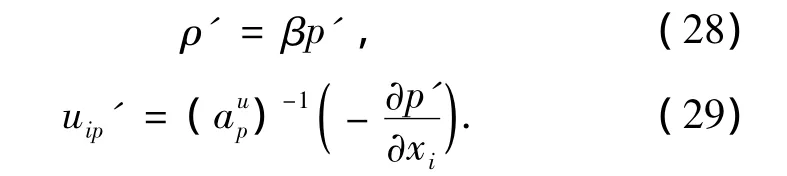
将式(28)、(29)代入式(23)，得面通量:

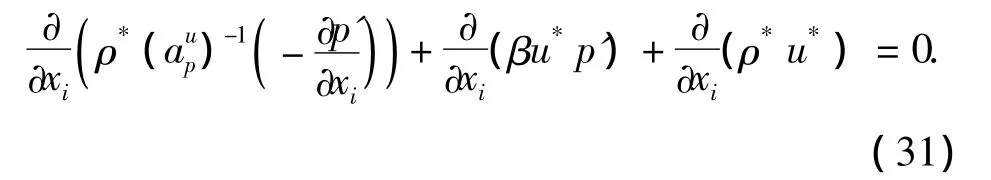
当流场计算达到收敛时，压力修正量趋近于0.用动量插值法［13］求界面上的速度，以便克服压力与速度的失耦.为了防止亚松弛因子的数值影响数值计算结果，动量插值时，动量方程不采用亚松弛.

3.3 SIMPLER算法

SIMPLER算法中压力修正值只用来修正速度，压力场是基于当前速度场由压力方程解得.与SIMPLE算法相比，SIMPLER算法多解一个压力方程，使压力场与速度场始终保持协调，故整体效率较高.SIMPLER算法计算步骤见文献［11-12］

稳态计算时，基于压力的算法不包含时间导数项，这时可以通过变量松弛和方程松弛使程序计算顺利收敛.变量松弛方程是显式的:

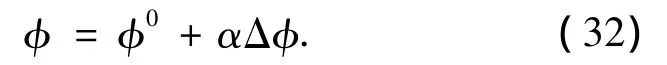
式中:α是松弛因子.方程松弛是隐式的:

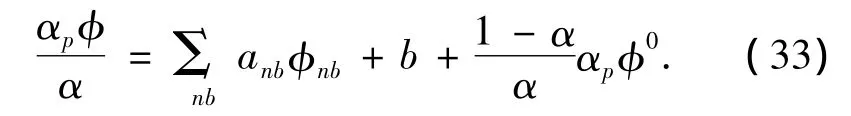
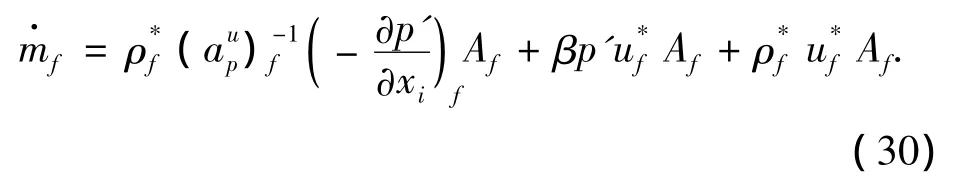
最终可得压力修正方程:

为了不破坏质量守恒，压力方程和压力修正方程不能采用方程松弛，而应采用变量松弛.

4 计算结果

4.1 圆弧凸包流动

凸包流动是一个内流问题.下壁面有凸包的管道无粘流动，长期以来被作为检验程序和计算方法的经典算例.圆弧凸包的弦长为1.0，高度为0.1(亚音速和跨音速计算)或0.04(超音速计算).

4.1.1 亚音速流动

给定圆弧凸包通道进口处的总温、总压及速度方向(马赫数为0.5)、出口处的静压.壁面采用无渗透滑移边界条件.图3表示计算区域中的马赫数分布.由图4可见，马赫数关于圆弧凸包通道的弦线中点具有良好的对称性.

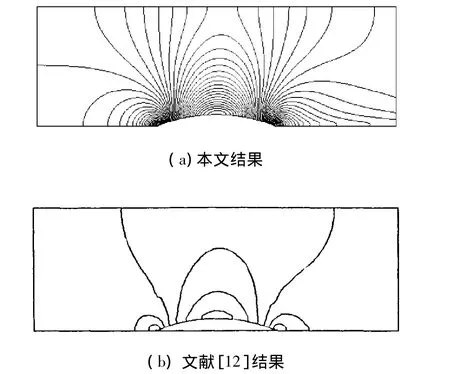
图3 亚音速流动计算区域中的马赫数分布Fig.3 Mach number distribution of subsonic flow calculation region

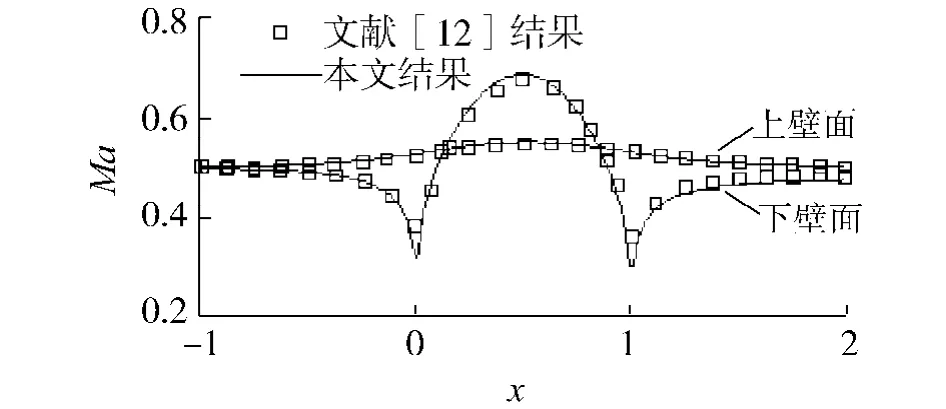
图4 亚音速流动时的壁面马赫数分布Fig.4 Surface Mach number distribution for subsonic flow

4.1.2 跨音速流动

进口边界条件设定中隐含着马赫数为0.675，其余边界条件的设定同亚音速流动.

如图5(a)所示，激波捕捉不明显，这是因为一阶上风格式将激波摸平.如图5(b)所示，用TVD格式捕捉激波，其效果比图5(a)好.而在文献［12］的计算结果中，激波基本被抹平了.这体现了本文采用的TVD格式对流场中的间断具有良好的捕捉能力.图6计算结果表明流场中出现了超音速区，马赫数关于圆弧凸包的弦线中点不再具有良好的对称性，最大马赫数点向下游方向偏移.

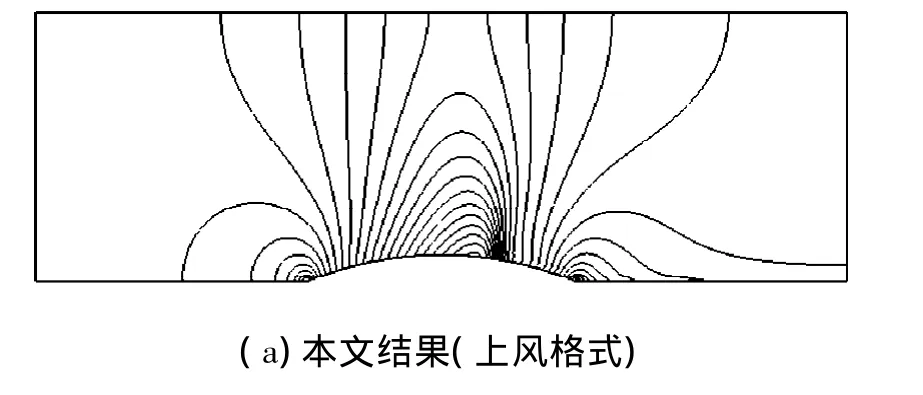
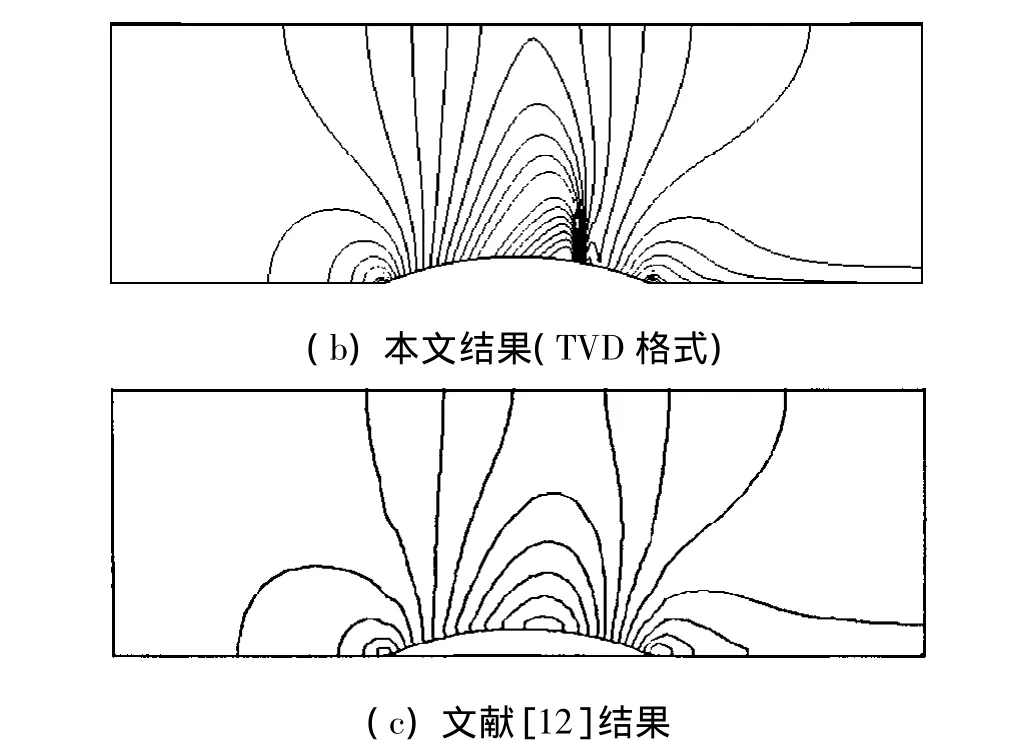
图5 跨音速流动计算区域中的马赫数分布Fig.5 Mach number distribution of transonic flow calculation region

图6 跨音速流动时的壁面马赫数分布Fig.6 Surface Mach number distribution for transonic flow

4.1.3 超音速流动

给定进口边界处的静温、静压和进口速度;出口边界，外插所有流场变量;上下壁面采用无渗透滑移边界条件.以进口的条件初始化流场.如图7所示，运用上风格式计算所得的结果与文献［12］相似，而运用TVD格式计算所得的结果表明激波捕捉比较清晰，圆弧凸包前沿处有一个前缘压缩波系，它同上壁面相交并反射后，又与后缘压缩波系相交.TVD格式对马赫数等参数分布梯度很大的流动现象具有良好的捕捉特性.如图8所示的壁面马赫数分布中，压缩波系从端壁发出，被端壁反射，从而形成陡峭参数分布.

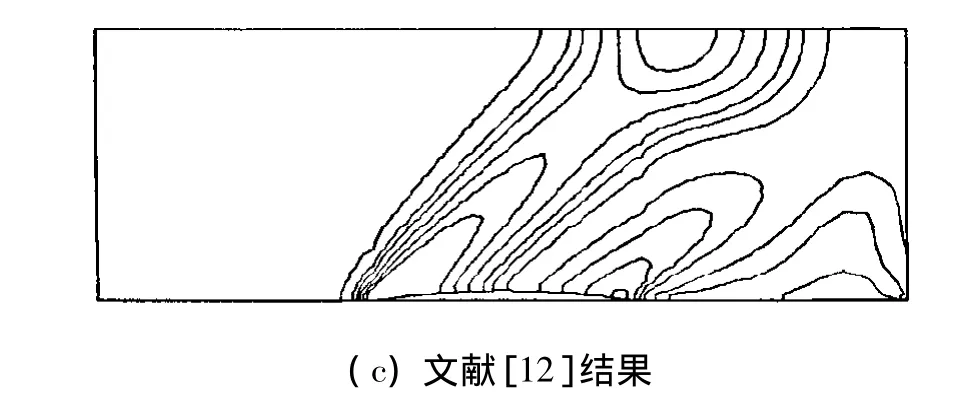
图7 超音速流动计算区域中的马赫数分布Fig.7 Mach number distribution of supersonic flow calculation region

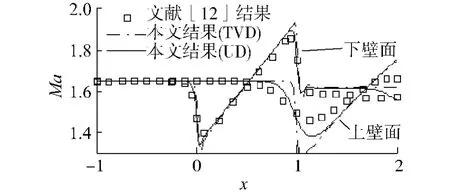
图8 超音速流动时的壁面马赫数分布Fig.8 Surface Mach number distribution for supersonic flow

4.2 平面叶栅

本文计算了一个平面叶栅内部流场.计算网格如图9.给定进口处的总压169.6 kPa、总温293 K和速度方向(垂直于进口方向)，出口处的静压140 kPa.计算采用高雷诺数k-ε湍流模型.图10给出了平面叶栅的马赫数分布.

图9 平面叶栅网格Fig.9 Plane cascade grid

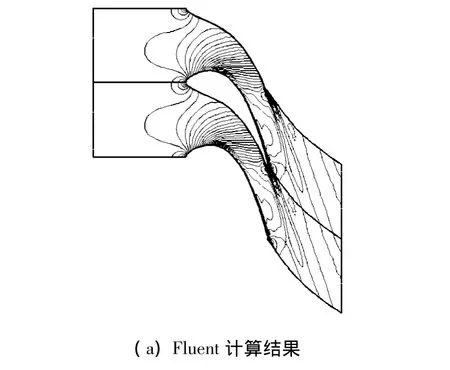
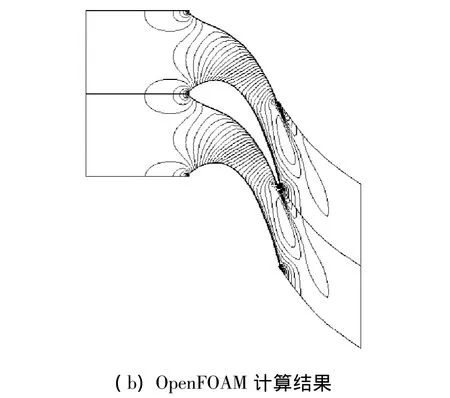
图10 平面叶栅的马赫数分布Fig.10 Mach numer distribution of plane cascade

5 结论

基于OpenFOAM程序，用SIMPLER算法模拟亚音速、跨音速和超音速条件下的圆弧凸包流场，然后模拟平面叶栅流场.结果表明:

1)文中采用TVD格式能够很好捕捉激波，并且具有很高的模拟精度;

2)针对不同马赫数进口求解，说明经过可压缩推广的SIMPLER算法适用于任何马赫数流场计算;

3)平板叶栅计算与其他CFD软件计算比较，可利用OpenFOAM程序开发的求解程序来替代标准商业CFD求解软件包.

本文只对二维的算例进行了考核，今后工作中将增加对三维计算的算例的考核，使程序满足实际计算的需要.

［1］黄典贵.基于Roe格式的可压与不可压流的统一计算方法［J］.应用数学和力学，2006，27(6):669-675.

HUANG Diangui.Unified computation of flow with compressible and incompressible fluid based on Roe＇s scheme［J］.Applied Mathematics and Mechanics，2006，27(6):669-675.

［2］严明，赵秋颖，梁磊.预处理方法在叶轮机械三维数值模拟中的应用［J］.航空动力学报，2007，22(1):41-47.

YAN Ming，ZHAO Qiuying，LIANG Lei.Application of preconditioning method in 3D numerical simulation of turbomachinery［J］.Journal of Aerospace Power，2007，22(1): 41-47.

［3］周红梅，苏莫明，任雄.基于可压缩SIMPLE算法的叶栅通道湍流流场的数值模拟［J］.汽轮机技术，2007，49 (4):266-268.

ZHOU Hongmei，SU Moming，REN Xiong.Numerical investigation of turbulent flow for cascade passage based on compressible SIMPLE arithmetic［J］.Turbine Technology，2007，49(4):266-268.

［4］伏晓艳，高歌.求解可压缩流动的同位网格SIMPLE方法研究［J］.航空动力学报，2007，22(10):1674-1677.

FU Xiaoyan，GAO Ge.Study of SIMPLE algorithm for compressible flows on non-staggered grids［J］.Journal of Aerospace Power，2007，22(10):1674-1677.

［5］WELLER H，TABOR G，JASAK H.A tensorial approach to computational continuum mechanics using object-oriented techniques［J］.Computers in Physics，1998，12(6):620-631.

［6］MANGANI L.Development and validation of a C++object oriented CFD code for heat tansfer analysis［C］// ASME-JSME Thermal Engineering and Summer Heat Transfer Conference.Vancouver，2007:1-16.

［7］MANGANI L，ANDREINI A.Application of an object-oriented CFD code to heat transfer analysis［C］//ASME Turbo Expo.Berlin，2008:1-13.

［8］李孙伟.OpenFOAM模拟风洞边界层风场［J］.山西建筑，2008，34(23):70-71.

LI Sunwei.Simulating boundary layer in wind tunnel using OpenFOAM［J］.Shanxi Architecture，2008，34(23):70-71.

［9］HARTEN A.High resolution schemes for hyperbolic conservation laws［J］.Journal of Computational Physics，1983，49(3):357-393.

［10］JASAK H.Error analysis and estimation for the finite volume method with applications to fluid flows［D］.London: Imperial College of Science，Technology and Medicine，1996:97-100.

［11］陶文铨.计算传热学的近代进展［M］.北京:科学出版社，2000:159-200.

TAO Wenquan.Modern development of computational heat tansfer［M］.Beijing:Science Press，2000:159-200.

［12］KARKI K C，PATANKAR S V.Pressure based calculation procedure for viscous flows at all speeds in arbitrary configurations［J］.AIAA Journal，1989，27(9):1167-1174.

［13］RHIE C M，CHOW W L.Numerical study of the turbulent flow past an airfoil with trailing edge separation［J］.AIAA Journal，1983，21(11):1525-1532.

［14］TRAORE P，AHIPO Y M，LOUSTE C.A robust and efficient finite volume scheme for the discretization of diffusive flux on extremely skewed meshes in complex geometries［J］.Journal of Computational Physics，2009，228(14): 5148-5159.

［15］CHEN Hailong，DAI Shaoshi，LI Jia，YAO Xiongliang.Three-dimensional numeriacal simulaition of the flow past a circular cylinder based on LES method［J］.Journal of Marine Science and Application，2009，8(2):110-117.