近似最优的粗糙集连续属性离散化断点选择方法＊

田树新 吴晓平 王红霞 张 丽

（海军工程大学电子工程学院1） 武汉 430033）

（91829部队2） 大连 116041） （海军工程大学图书馆3） 武汉 430033）

0 引 言

粗糙集理论是由波兰理工大学的Z.Pawlak教授于20世纪80年代提出的一种新的处理模糊和不确定性知识的数学工具.目前，在机器学习、决策分析、模式识别与数据挖掘、故障诊断等领域粗糙集理论得到了广泛的应用.但是在大量的决策问题中，决策信息系统中的属性值往往是连续的，而粗糙集方法只能处理离散属性值.为了能够从这些含有连续属性的数据库中取得好的数据样本，得到简洁且有效的规则，常常需要对连续属性进行离散化.离散化结果将会减小系统的存储空间的实际需求，加快后继数据挖掘和机器学习算法的运行速度，减小后继算法的空间开销，提高分类精度.然而，连续属性的最优离散化是一个NP完全问题［1］，采用不同的离散化方法，结果也往往存在差异.

在离散化的应用和研究中，贪心及其改进算法、基于属性重要性、基于信息熵和基于聚类的离散化方法是四类常用的方法［2］.H.S.Nguyen等人提出了一种连续属性离散化的贪心算法，并在此基础上出现了一些改进算法，这类算法考虑了属性间的互补性和相关性，能够在不分明关系保持不变的条件下得到断点数较少的结果断点集，但是计算代价较大，时间复杂度为n3×k；基于属性重要性的离散化算法首先计算条件属性的重要性，然后根据属性重要性由小到大对条件属性进行排列，并依次求每个条件属性的断点，这类算法往往会产生过多的断点，时间复杂度为n2×k；基于信息熵的离散化算法是从条件属性的候选断点中选择结果断点，通过逐步挑选信息熵最小的候选断点，根据属性值大于或小于断点值把所有等价类划分为两部分，当达到某种终止标准时，停止挑选候选断点.由于在计算信息熵时需要对数据集的对象按照决策值分类，属性集决策值分类多少，直接影响算法的计算代价，时间复杂度为n3×k.基于聚类的离散化算法分为整体离散化和单个属性离散化，这类算法不需要设置参数，得到的断点集也较好，但是算法的计算代价较高，时间复杂度（n×k）2.

文献［3］在保证信息系统分辨关系的前提下，采用基数最小的断点集合对系统进行的离散化就是基于粗糙集理论的最优离散化.从这个定义不难发现，对一个给定的信息系统，存在一种或多种最优的离散化结果.由于已经证明连续属性的最优离散化问题是一个NP完全问题，因此本文试图获得近似最优的离散化结果.

1 相关概念与离散化问题描述

1.1 相关基本概念

粗糙集理论是以不可分辨关系划分所研究论域的知识，形成知识表达系统，利用上、下近似集逼近描述对象，通过知识约简，从而获得最简知识，下面介绍其基本概念.

定义1 一个信息系统定义为一个如下四元组S＝（U，R，V，F）.式中：U＝｛x1，x2，…，xn｝为对象集，即论域；R为属性集合，若属性集可分为条件属性集C和决策属性集D，即有R＝C∪D，且C∩D＝Ø，则该信息系统称为一个决策系统或决策表是属性值的集合，Vr表示属性r∈R的属性值范围；F∶U×R→V是一个信息函数，它指定U中每一个样本x的属性值.

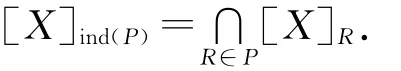
定义3 对于决策表S＝（U，C∪D，V，F）如果∃x1，x2∈U，使得x2∈［x1］C而x∉2［x1］D则称决策表S是不相容的，否则称决策表是相容的.

定义4 条件信息熵［4］Hc（｛d｝｜C）

式中：U／IND（｛d｝）＝｛Y1，Y2，…，Ym｝，Yj称为决策类，U／IND（｛C｝）＝｛X1，X2，…，Xn｝）.条件信息熵能有效地度量条件向量的决策值分布情况.

1.2 离散化问题描述

决策表S＝（U，C∪D，V，F）.式中：C 为条件属性集D 为决策属性集.条件属性a的值域Va上的一个断点可以记为（a，c），其中a∈R，c为实数集.在值域Va＝［la，ra］上的任意断点集（又称断点区间）｛），），…，（a，）｝定义了Va上的一个分类Pa，pa＝，…，

离散化本质上可归结为利用选取的断点来对条件属性构成的空间进行划分的问题，把这个n（n为条件属性的个数）维空间划分成有限区域，使得每个区域中的 的决策值相同.假设某个属性有m个属性值，则在此属性上就有m－1个断点可取，随着属性个数的增加，可取的断点数将随着属性值的个数呈几何增长.选取断点的过程也是合并属性值的过程，通过合并属性值，减少属性值的个数，减少问题的复杂度，这也有利于提高知识获取过程中所得到的规则知识的适应度.根据选取断点的过程是从包含所有断点的断点集中逐步删除不必要的断点得到离散化结果，还是一开始设断点集为空集，逐步增加候选断点得到离散化结果，可以把离散化过程分为“逐步删除断点”和“逐步增加断点”的离散化算法.

等距离划分算法、等频率划分算法、布尔逻辑和粗糙集理论相结合的离散化算法及其相应的改进算法、基于属性重要性的离散化算法、基于信息熵的离散化算法［5－7］和基于聚类的离散化算法［8］等都属于“逐步删除断点”的离散化算法；NaiveS－caler算法等属于“逐步增加断点”的离散化算法［9］.

对于离散化方法没有统一的衡量标准，本文主要遵循的如下原则：（1）离散化后属性的结果尽可能地简单，即离散化后的断点区间尽可能少；（2）离散化处理应该尽可能保证经过离散化处理后得到的数据集的一致性与原始数据集的一致性接近.

2 近似最优的离散化算法

近似最优的离散化方法是选取较少的断点来划分条件属性构成的空间，首先选择重要性程度最高的条件属性，根据启发式规则逐步增加断点，直到断点划分的区间相容度一致，最后合并具有相同决策值的相邻区间，删除多余断点.为了能够划有效分决策表，可能需要选用几个相对重要的条件属性依次进行再划分.

算法步骤.

符号标记 CUT为选取的断点的集合；L为实例被断点集合CUT所划分成的等价类的集合；H为决策表信息熵.

步骤1 比较条件属性重要性，首先对最重要的属性（记为条件属性a）进行划分.

步骤2 条件属性a的属性值按递增顺序排列为La＝＜…＜＝Ra.

步骤3 根据第二步排序的结果选取断点的启发式规则：

步骤3.1 若每个属性值均不相同，则取中间点为第一个断点；

步骤3.2 若有部分属性值相同，则按照第二步排序依次计算每个取值出现的频率，记为，当第j个属性值的频率与其他频率的关系满足

时，则按照下面的规则增加断点；

步骤4 增加断点直到决策表相容.

步骤5 检查相邻2个断点对应的熵值和决策值是否相同，若相同则删除一个断点，2个区间合并为一个区间，更新断点集CUT.

步骤6 若同一区间对应的决策表对应的决策值不同，则选取次重要的条件属性，转到步骤2，依次类推，直到根据需求，决策表能够划分.算法结束.

分析 设X⊆U，其实例个数记为｜X｜，其中决策属性为j（j＝1，2，…，r（d））的实例个数为kj，定义此子集的信息熵为

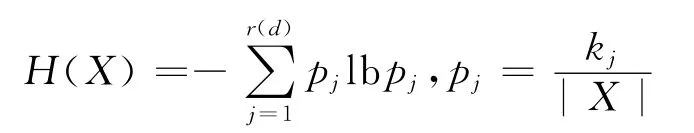
一般有H（X）≥0.信息熵H（X）越小，说明集合X中个别决策属性值占主导地位，因此混乱程度越小，特别有当且仅当X中实例的决策属性值都相同时H（X）＝0.文中选用的启发式规则保证了此离散化算法不改变决策表的相容度.与基于信息熵的离散化方法［6］结果趋于一致.

文献［6］中候选断点为

并计算每个候选断点划分两个区间的信息熵，它虽然考虑了粗集理论的相容度，但是候选断点非常多，需要大量的信息熵的计算，计算复杂度比较高（计算复杂度为nk2m2，n为论域元素个数，k为属性个数，m为条件属性取值平均个数）.本文在最坏情况下，即每个条件属性取值均不相同的情况下，计算复杂度nk2m2；当属性值出现的频率比较高或者样本数比较多时，计算复杂度将远远小于nk2m3.

3 实验结果

实验1 选择UCI数据库中的“Iris Plants Database”数据来对所述方法进行验证分析.数据库中的样本数有150个，条件属性4个，决策属性1个，决策分类为3个.条件属性4的属性值排序及属性值出现的频率如表1.

表1 属性值、出现频率及断点插入次序之间的关系

表1中第一行和第三行的数据是根据算法步骤3.2中“第j个属性值的频率与其他频率的关系”计算获得，对于“Iris Plants Database”中断点数只要简单的排序和频率关系计算就能获得与文献［2，6，7］相同的断点数，但是计算量远远小于文献［2，6，7］的计算量.

实验2 选取基于属性重要性算法的离散化方法，基于信息熵的离散化方法，和本文的算法进行性能分析比较.实验的数据是从UCI机器学习数据中选取的3个只包含连续属性的数据集，分别是Iris，Wine，Heart.实验过程为：先将数据集中的2／3数据作为训练样本，其他的1／3数据作为测试样本；再对训练样本进行离散化，得到断点集和离散化后的训练样本.最后用训练样本的断点集对测试样本进行测试.3种算法实验结果如表2.

表2 三种算法实验结果

分析：本文算法选用的条件属性比较多，同时在选条件属性时，应用了数据集的领域知识，所以相对其他算法，有较高的识别率和较低的误识率.

4 结 论

本文所提算法是以基于信息熵的算法为基础，选用有效的启发式规则，为寻求最少断点数的离散化方法提供依据.对某个重要属性条件先进行离散化，当熵降变化不大时，在此基础上再选用次重要的属性条件进行离散化，以保证确定恰当的区间数使得离散效果最好.

［1］Nguyen H S，Skowron A.Quantization of real values attributes：rough set and boolean reasoning approach［C］／／Proc.of the Second Joint Annual Conference on Information Sciences，Wrightsville Beach，North Carolina，Sept 28 －Oct 1，1995：34－37.

［2］刘业政，焦 宁，姜元春.连续属性离散化算法比较研究［J］.计算机应用研究，2007，24（9）：28－30.

［3］赵 军，王国胤，吴中福.基于粗集理论的数据离散化新算法［J］.重庆大学学报：自然科学版，2002，25（3）：18－21.

［4］王立宏，孙立民，孟佳娜.数值离散化中粒度熵与分类精度的相关性［J］.重庆大学学报，2008，31（1）：57－60.

［5］沈永红，王发兴.基于信息熵的粗糙集属性离散化方法及应用［J］.计算机工程与应用，2008，44（5）：221－224.

［6］谢 宏，程浩忠，牛东晓.基于信息熵的粗糙集连续属性离散化算法［J］.计算机学报，2005，28（9）：1 570－1 574.

［7］李春贵，王 萌，原庆能.基于启发式信息熵的粗集数值属性离散化算法［J］.广西科学院学报，2007，23（4）：235－237.

［8］苗夺谦.Rough Set理论中连续属性的离散化方法［J］.自动化学报，2001，27（3）：296－302.

［9］侯利娟，王国胤，聂 能.粗糙集理论中的离散化问题［J］.计算机科学，2000，27（12）：89－94.