多约束条件下的机器人时间最优轨迹规划

钱东海，马文罗，汪建伟，王伟东

QIAN Dong-hai1,MA Wen-luo1,WANG Jian-wei2,WANG Wei-dong1

（ 1. 上海大学 精密机械工程系 上海 200072；2. 浙江中烟工业有限责任公司，杭州 310008 ）

0 引言

机器人运动规划通常分为路径规划和轨迹规划上下两级[1]。路径规划由机器人的任务规划器完成，用于在笛卡尔空间中或关节空间中产生一无碰撞的几何路径。轨迹规划则是按照一定的性能指标确定沿着该几何路径运动时各关节的速度、加速度、加加速度、控制力矩的时间曲线。机器人的时间最优轨迹规划是指以时间最短作为性能指标，并在满足各种约束的条件下优化机器人的运动轨迹，使机器人沿规定路径运动的时间最短。

由于轨迹规划是机械人控制的基础，其性能对机器人的工作效率，运动平稳性和能量消耗具有决定性意义，因此在过去十几年中，轨迹规划一直是机器人研究中的一大热点。轨迹规划主要分成以下几类：时间最优轨迹规划，能量最优轨迹规划，冲击最优轨迹规划，以及混合最优轨迹规划。

时间最优轨迹规划在文献中是最早提出的，因为可以大大提高生产的效率[2～5]。能量最优适合于机器人电源供应受到限制的场合，此时利用能量法进行轨迹规划，产生光滑轨迹是非常理想的[6,7]。机器人运动过程中的冲击不但会影响运动轨迹的光滑性和精确度，而且会损耗零部件，降低使用寿命，因此冲击最优轨迹规划的研究同样也是非常有意义的[8,9]。综合考虑以上时间、能量、冲击的约束条件，则构成混合最优轨迹规划，如时间-能量最优、时间-冲击最优等。文献[10～12]分别从时间能量合成最优和时间冲击最优来规划机器人的运动轨迹，但这种方法需要精确的动力学数学模型，因动力学方程求解计算量大，以及动力学方程参数难以精确确定使得上述算法受限于实际应用。

已有文献针对上述优化问题，在设定约束条件时，在笛卡尔空间中都只考虑各离散路径点的位置信息，而没有对离散路径点处速度方向这一约束进行相应考虑，从而造成机器人实际运动路径与理想所需运动路径偏差较大。本文采用三次多项式对运动轨迹进行插值，建立优化模型时，除了在关节空间中考虑各关节的速度、加速度、加加速度等约束条件，同时考虑笛卡尔空间中机器人在各离散路径点处速度方向所应满足的约束条件。实现了在不增加离散路径点数量的条件下，使得规划的路径精度得到了很大的提高。最后，本文提出的算法被应用于一剪带机器人的轨迹规划，验证了该算法的有效性和可行性。

1 利用三次样条构造机器人运动轨迹

本文研究最优轨迹规划策略时，假定机器人已通过路径规划，在笛卡尔空间中形成一无碰撞的运动路径，并依据常规假定该路径由一系列离散路径点构成。

利用机器人运动学逆解在关节空间中求得与离散路径点相对应的关节节点序列（假定共n个节点），通过一系列的三次样条曲线来插值连接这些关节节点。假定机器人具有N个关节，并设 qj,1,qj,2,…,qj,n为关节j(1≤j≤N)在各节点处的位移，{t1,t2,…,tn}为机器人运动至各节点处的时间序列。定义Qj,i(t)、Q'j,i(t)、Q''j,i(t)、Q'''j,i(t)分别为关节j在时间间隔[ti,ti+1]内位移、速度、加速度、加加速度的数学表达式，并且关节j在初始时刻t=t1的关节速度值、加速度值以及终止时刻t=tn的关节速度值、加速度值都是已知的[5]。

由于Qj,i(t)是时间t的三次多项式，其二阶导数Q''j,i(t)是时间t 的一次多项式，于是得到：

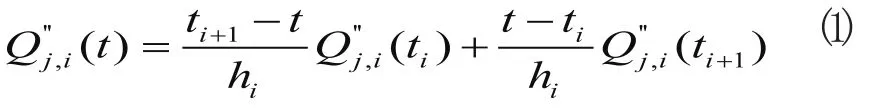
对式(1)的Q''j,i(t)表达式连续进行积分两次，并利用已知条件Qj,i(ti)=qj,i，Qj,i(ti+1)=qj,i+1，可确定积分过程中的两个积分常数，整理后得到Qj,i(t)的表达式为：

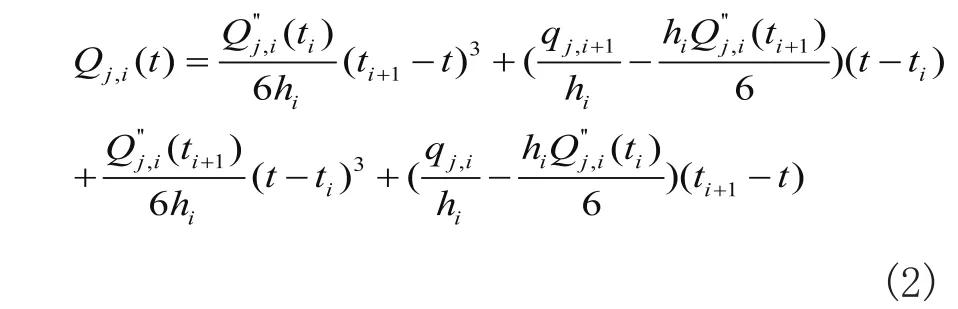
对公式(2)进行一次微分和三次微分，可以得到如下表达式：

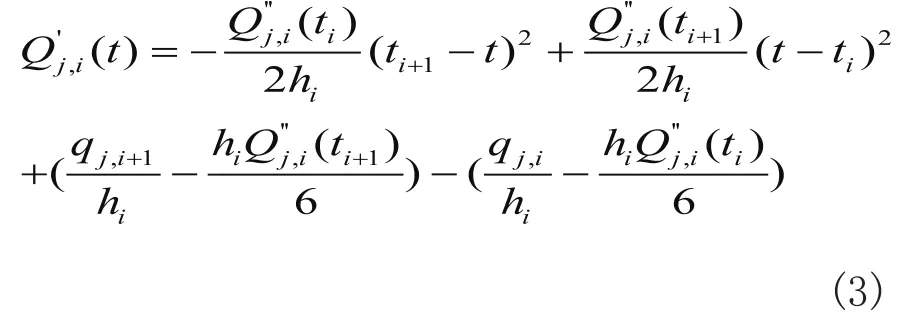
对于公式(1)～(4)，只要求出公式中Q''j,i(ti)在各时间节点(t=t1,t2,...,tn)处的值，公式(1)～(4)的方程便可以唯一确定。在ti=t1、ti=tn两端点处，速度、加速度为给定值，利用公式(3)，并基于速度连续性条件联立方程，可方便地求出(t=t1,t2,...,tn-1)时Q''j,i(ti)的值。

公式(1)～(4)的方程确定以后，最优轨迹规划就转化为满足上述4个方程，并满足关节空间和笛卡尔空间的约束条件，求取时间序列t1,t2,...,tn的值，使得总的运动时间（即tn）为最小。

2 最优轨迹规划模型建立

2.1 关节空间中所应满足的约束条件

关节空间中，考虑各关节所能达到的最大速度、最大加速度的物理限制，同时考虑各关节所能允许的最大冲击限制，定义各关节的速度、加速度、加加速度的约束条件如下：

其中j=1,2,…,N，i=1,2,…,n-1。VCj、WCj、JCj分别表示机器人第j个关节的最大速度、加速度和加加速度的值。

2.2 笛卡尔空间中所应满足的约束条件

一般来讲，时间最优轨迹规划时，均需满足公式(5)所要求的约束条件，但是对于需要沿给定路径运动的机器人，上述约束条件是不够的。上述约束条件只从机器人各关节所能达到的极限运动状态加以约束，并没有考虑机器人运动路径的精度。本文针对笛卡尔空间中沿给定路径运动机器人的时间最优轨迹规划问题，分析此类机器人运动时所应满足的约束条件，改进优化设计的模型，解决现有时间最优轨迹规划算法在解决此类问题中存在的不足。

对于沿给定路径运动的机器人，机器人在任意时刻运动速度的方向都应与机器人当前所在位置处路径切线的方向一致，这样才能保证机器人不偏离给定路径。反应在机器人时间最优轨迹规划上，应将机器人瞬时速度与运动路径切线之间存在的约束引入到时间最优轨迹规划数学模型中。

假定f1(x)、f2(x)为笛卡尔空间中的两曲面，其中x=[x1,x2,x3]T。机器人的运动路径由两曲面的交线确定，曲面f1(x)、f2(x)的法线向量为：

机器人末端的瞬时速度为：

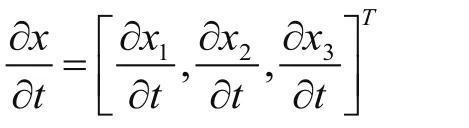
机器人沿由f1(x)、f2(x)所确定的路径运动时，其速度方向与两曲面的法线垂直，故存在：

式(6)构成了笛卡尔空间中沿给定路径运动机器人在进行时间最优轨迹规划时所应满足的约束条件。

2.3 时间最优轨迹规划目标的建立

机器人的运动速度直接影响到作业的效率，机器人时间最优轨迹规划就是在满足约束的条件下，使得机器人从起点到终点的运动时间为最短。也即对于公式(1)～(4)中的hi，使得：

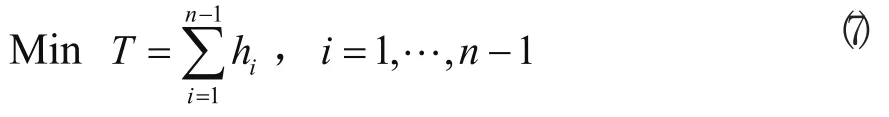
本文采用序列二次规划法来求解式(1)～(7)所描述的非线性约束优化问题。序列二次规划的思想是通过构造拉格朗日函数，将一个约束优化问题转化为一系列无约束优化问题来求解。由于序列二次规划方法是一种局部最优算法，因此初始值的选择很重要，初始值选择不合理，不仅影响到优化算法的搜索效率，并有可能得到非最优解。序列二次规划法在优化设计已经得到广泛应用，可利用成熟的软件直接进行求解。

3 算法实例验证

3.1 超二次曲线的数学描述

为验证本文提出的算法，将在二维平面中，驱动直角坐标机器人沿着圆角矩形运动，分析其沿特定路径运动时的偏差，并和已有算法做一对比分析。

圆角矩形本质为一超二次曲线，其方程为：

圆角矩形的形状会随着指数 的变化而变化，如图1所示。

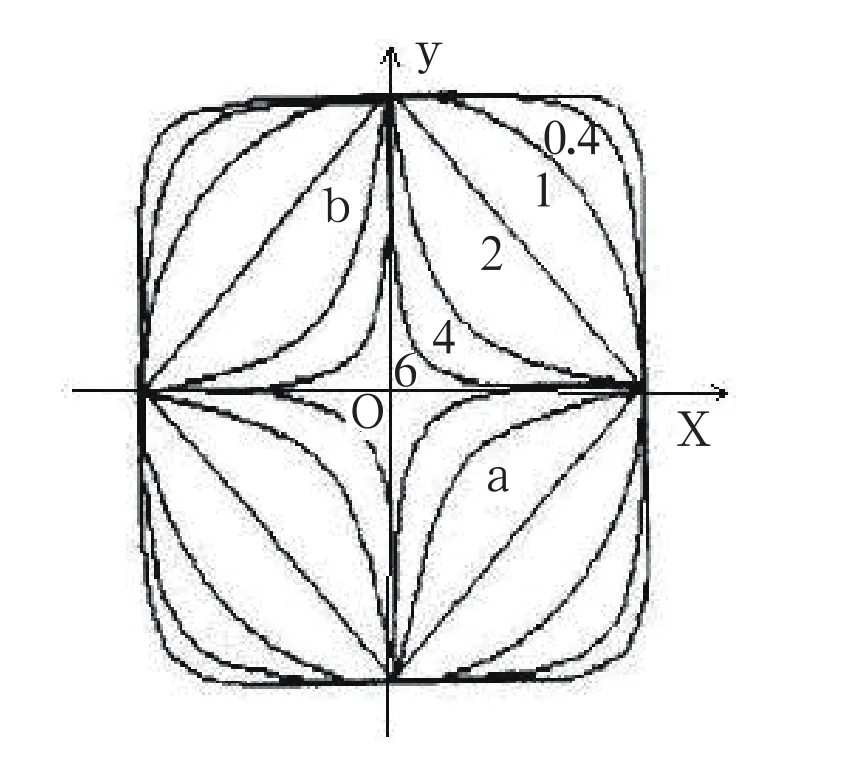
图1 不同的指数对超二次曲线的影响

图1中α、b分别为矩形的半长和半宽。可以看出，当指数ε变小时，圆角矩形的四个顶点变尖，当ε趋向无穷小时，圆角矩形就变成矩形。本文中令ε=0.5、α=b=10，驱动机器人沿圆角矩形x4+y4=104进行运动，其中单位为厘米。

3.2 试验结果与分析

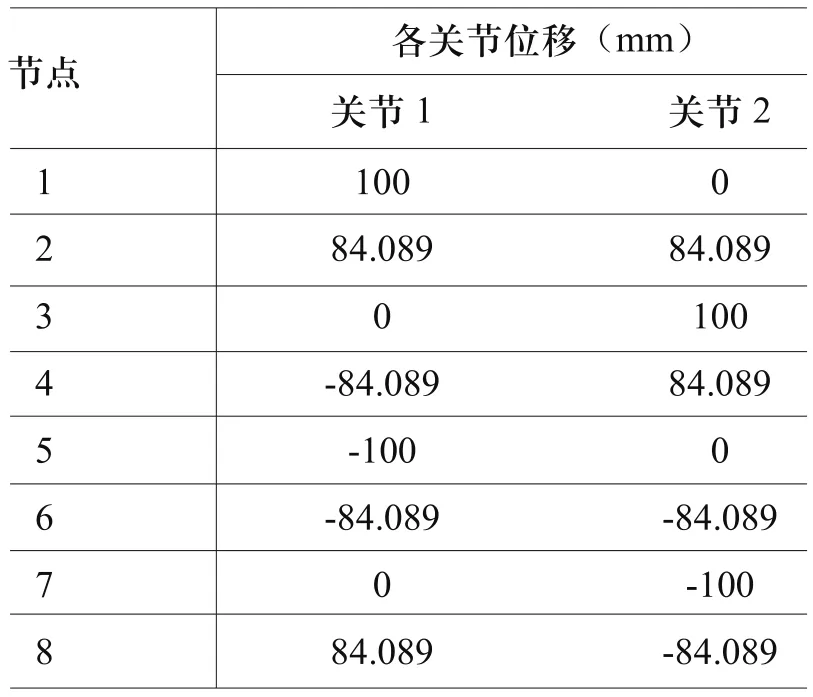
表1 关节位移序列

上述运动路径中，取圆角矩形与坐标轴的四个交点，以及圆角矩形的四个顶点，作为离散路径点，控制机器人沿圆角矩形的运动。因采用的是直角坐标机器人，笛卡尔空间和关节空间是统一的，8个离散路径点在笛卡尔空间，也即关节空间中的位置如表1所示。

各关节的速度、加速度、加加速度的约束如表2所示。并假定机器人在起始点和终止点的速度、加速度的值均为0。

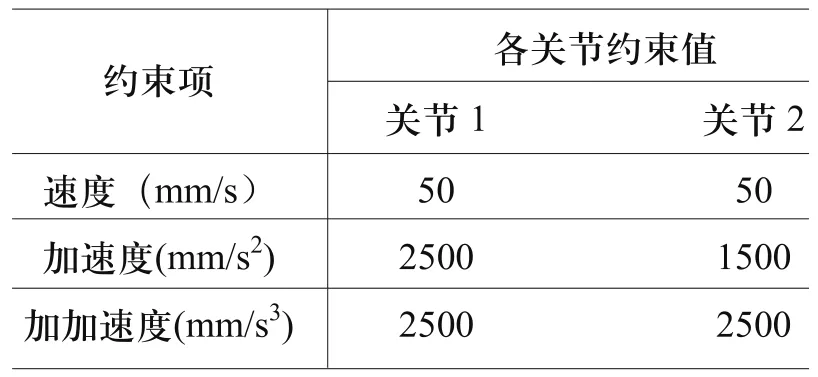
表2 机器人速度、加速度、加加速度约束

利用文献[5]给出的算法对机器人进行时间最优轨迹规划，得到的实际运动路径与给定圆角矩形的最大偏差为4.32毫米，所需的运动时间为20.1754秒。

采用本文所提出的算法，确保机器人在各离散路径点处满足由曲线方程所决定的速度约束条件，得到的实际运动路径与给定曲线方程的最大偏差为0.4514毫米，所需的运动时间为41.2479秒。

通过对比可以看出：通过引入由曲线方程所决定的速度约束条件，机器人实际运动路径的偏差大大降低了，这在机器人弧焊、涂胶、切割等应用中具有很强的应用价值。通过比较，我们也发现采用本文提出的方法会使得运动的时间相应地增加，但这在弧焊、涂胶、切割等应用中不会成为应用的瓶颈。

图2 关节位移图

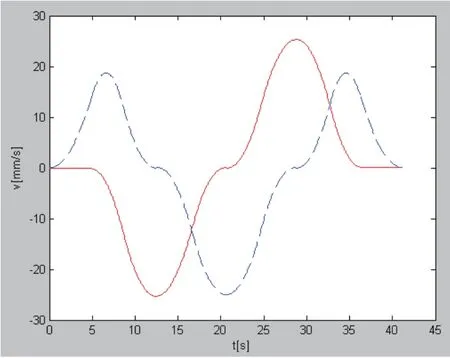
图3 关节速度图

图4 关节加速度图

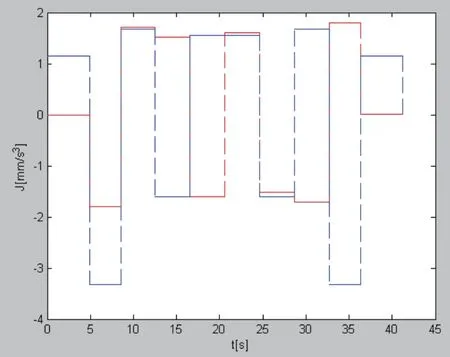
图5 关节加加速度图

图6 实际运动路径与给定路径偏差（采用文献[5]算法）

图7 实际运动路径与给定路径偏差（采用本文算法）

图2～5分别表示采用本文提出的算法进行时间最优轨迹规划，各个关节位移、速度、加速度、加加速度的曲线图。其中实线表示第一个关节，虚线表示第二个关节。图6和图7分别为采用文献[5]算法和采用本文算法时，实际运动路径与给定路径的偏差，其中实线表示实际运动路径，虚线表示给定的路径。

本文提出的算法还在自行研制的剪带机器人中得到了验证。如图8所示。

图8 剪带机器人

剪带机器人是一台能对纸箱外打包带进行自动剪断和回收的专用设备。其本质为一直角坐标机器人，共有三个自由度：第一、第二关节分别是平面内沿着X轴和Y轴方向进行平移的直线运动关节；第三个关节是绕Z轴回转的旋转关节。

4 结论

本文提出了一种机器人时间最优轨迹规划算法，该算法除了满足机器人常见的关节极限运动的约束条件，还保证机器人在各离散路径点处满足由给定路径所决定的速度约束条件，有效地减小了机器人实际运动路径与给定路径之间的偏差。最后试验验证了本文所提出算法的有效性和可行性。

[1] 钱东海,谭伟,赵锡芳.基于B样条路径的机器人时间最优轨迹规划[J].上海交通大学学报,1998,32(12)：29-32.

[2] Bobrow J E,Dubowsky S,Gibson J S.Time optimal control of robotic manipulators along specified paths[J].The international journal of robotics research,1985,4 (3)：3-17.

[3] Constantinescu D,Croft E A. Smooth and time-optimal trajectory planning for industrial manipulators along specified paths[J].Journal of robot systems,2000,17(5)：233-249.

[4] 杨国军,崔平远.机械手时间最优轨迹规划方法研究[J].中国机械工程,2002,13(20)：1715-1717.

[5] LIN C S,CHANG P R,LUH J Y S.Formulation and optimization of cubic polynomial joint trajectories for Industrial robots[J].IEEE Transactions on Automation Control,1983,28(12)：1066-1074.

[6] Martin B J,Bobrow J E.Minimum effort motions for open chain manipulators with task dependent end effector con- straints[J].The international journal of robotics research,1999,18(2)：213-224.

[7] Jha K.Minimum energy based interpolation for interactive incremental well path design[J].Engineering computations,2004,21：676-691.

[8] Huang P F,Chen K,Xu Y S.Motion trajectory planning of space manipulator for joint jerk minimization[C].IEEE Inter- national conference on mechatronics and automation,China： Harbin,2007：3543-3548.

[9] Piazzi A,Visioli A.Global minimum-jerk trajectory planning of robot manipulators[J].IEEE Transaction On Industrial Electronics,2000,2000,47(1)：140-149.

[10]Shiller Z.Time-energy optimal control of articulated systems with geometric path constraints[C].IEEE International Conference on Robotics and Automation,1994,4：2680-2685.

[11]Gasparetto A,Zanotto V.A technique for time-jerk opti-mal planning of robot trajectories[J].Robotics and computer Integrated Manufacturing,2008,24(6)：415-426.

[12]Verscheure D,Demeulenaere B,Swevers J.Time-energy optimal path tracking for robots：a numerically efficient opti- mization approach[C].International Workshop On Advanced Motion Control,2008,1：727-732.