大型风力机复合材料叶片动态特性及气弹稳定性分析
刘 伟,尹家聪,陈 璞,苏先樾
(北京大学力学与空天技术系湍流与复杂系统国家重点实验室,北京 100871)
0 引言
随着现代风力发电技术的日益成熟,全球风电产业近年来发展势头良好,大功率、兆瓦级风力发电机大量投入使用。与此同时,风力发电机的空气动力学特性及其结构优化设计也逐渐受到研究人员的广泛关注。叶片作为风力发电机的核心部件,其良好的结构特性是整个机组实现长期安全高效运行的前提,因此风机叶片的结构设计与分析是风机设计的重要环节。风机叶片一般展向长、弦向短,因而当前多数风机叶片的结构分析及优化设计研究均采用近似梁模型进行[1-2]。然而,由于目前大型风机的叶片普遍采用各种具有轻质高强特点的纤维增强复合材料制成,从整体上叶片可以看成是一种复杂薄壁结构。此时采用近似梁模型进行叶片结构分析,其结果可能无法满足精度要求[3]。此外,近似梁模型虽然能够在一定程度上反映叶片的整体性能,却无法揭示叶片的细节结构特性,如叶片在气动载荷下可能的局部屈曲[4]。
本文探索大型复合材料叶片三维壳模型的快速参数化建模技术,以及利用三维壳模型进行的叶片结构动态特性分析及静气弹稳定性分析。针对某初步设计的1.5MW风机叶片,首先采用参数化建模技术建立风力机复合材料叶片三维壳模型,并在此基础上对叶片的固有动力学特性进行分析,其中旋转工况下的分析考虑了离心力导致的应力刚化及旋转软化等附加效应的影响。然后,通过编制插值程序解决叶片气动力计算网格与结构计算网格不匹配问题,将CFD计算所得叶片表面分布压力导算到叶片结构计算有限元模型上,并以此为载荷对叶片进行静气弹稳定性分析,预测叶片发生局部屈曲的可能性及其发生的位置。
1 参数化建模
风机叶片的外形与内部结构较为复杂,一般由前缘、后缘、梁帽、腹板等不同区域组成的,不同的区域具有不同的复合材料铺层,因此在结构分析的三维壳模型建模过程中必须把叶片壳体按照铺层方式的不同分割为不同的材料面,以便对其赋予各自的复合材料参数。
本文利用计算几何方法,编制Matlab参数化建模程序。程序通过读取叶片控制截面翼型数据、沿展向分布的弦长、扭转角数据以及叶片各部分的复合材料铺层等各种几何、材料信息,自动输出通用有限元软件ANSYS能够读取的APDL命令流文件,由此快速建立叶片的三维几何模型。
以某初步设计的1.5MW风机叶片作为例,该风机叶片长度为40.5m,额定转速为17.2r/min。叶片典型翼型截面如图1所示。根据复合材料铺层方式的不同,上下表面各被分为5段:后缘加强层、后缘夹芯层、梁帽、前缘夹芯层以及前缘加强层。该叶片有前、后两个腹板。
采用本文所发展的参数化建模技术建立该风机的三维壳模型,如图2所示。由于各部分的铺层差异,叶片的外壳和前后腹板共被分作357个材料面。
在参数化建模的基础上,选择合适的单元尺寸,采用适合于复合材料层合板壳结构线性与非线性分析的八结点壳单元SHELL281对叶片的几何模型进行离散,生成的有限元模型如图3所示。最后,约束叶片根部圆周上所有结点自由度以模拟法兰盘对叶片的固定约束。

图1 某1.5MW风机叶片的典型截面示意图Fig.1 Schematic of a typical cross-section of the wind turbine blade

图2 某初步设计的1.5MW风机叶片三维模型Fig.2 Three-dimensional geometric model of the wind turbine blade

图3 某初步设计的1.5MW风机叶片有限元模型Fig.3 Finite element shell model of the wind turbine blade
2 模态分析
风机正常运行过程中,叶片处于旋转状态,其在旋转坐标系中的振动方程为:
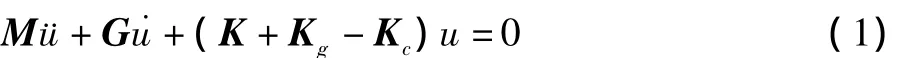
式中M,K分别为叶片的质量和刚度矩阵。Kg和Kc分别是离心力导致的刚度矩阵改变,与转速的平方成正比。离心力的这两种作用在有限元分析中分别被称为“应力刚化效应”和“旋转软化效应”。G是由科氏力引起的,与转速成正比。计算表明:由于大型水平轴风力机转速一般较低,G对叶片固有频率的影响十分微弱,可以忽略。
利用上述参数化建模方法建立的1.5MW风机叶片有限元壳模型,在停机工况和17.2r/min额定转速工况下分别对叶片进行模态分析,结果如表1所示。从表1可知,由于该风机的额定转速仅为17.2r/min,离心力引起的应力刚化和旋转软化效应对叶片各阶模态频率的影响很小。
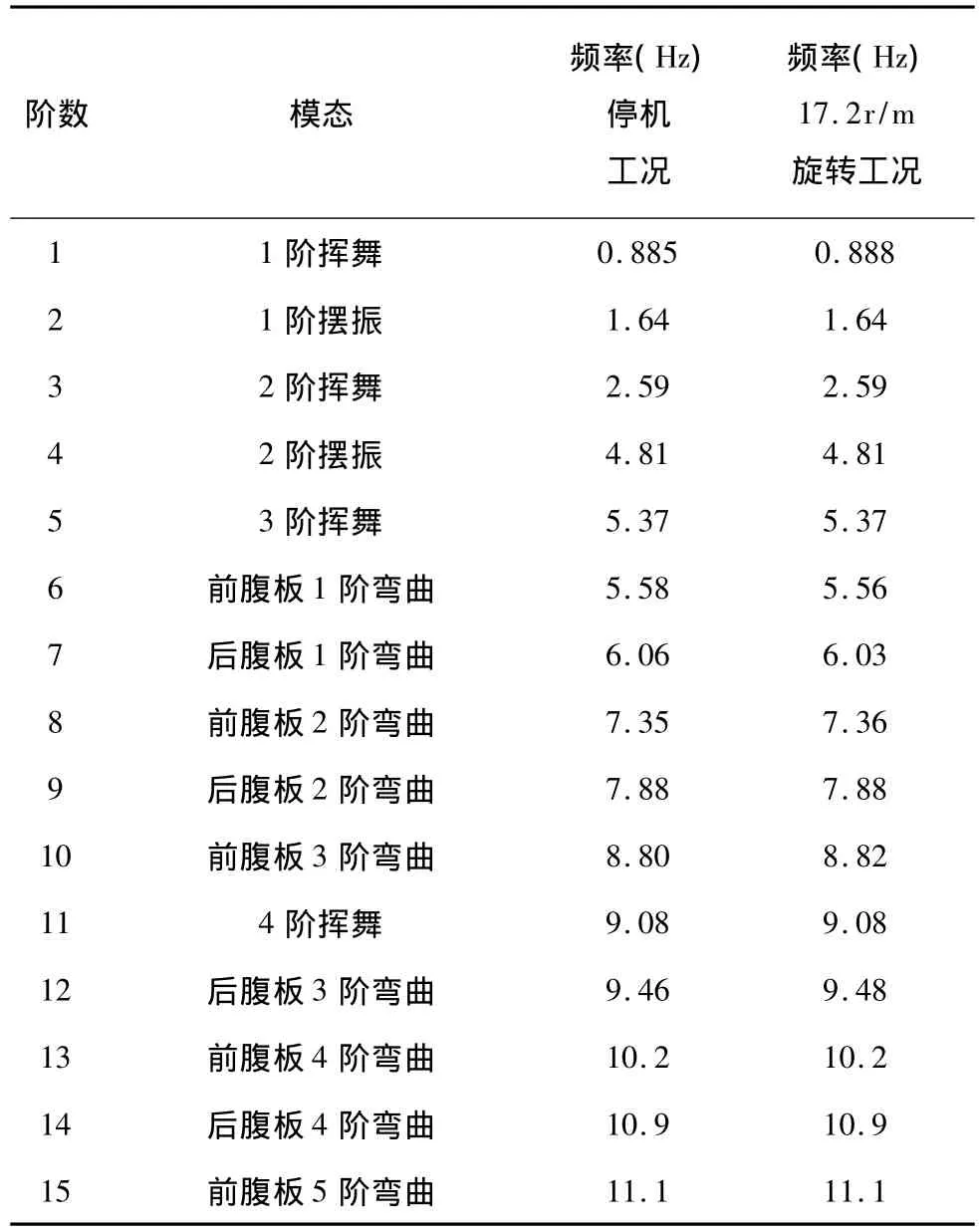
表1 某初步设计的1.5MW风机叶片前15阶模态的频率Table1 The lowest 15 natural frequencies of the wind turbine blade
值得注意的是,叶片的前15阶模态中,共有9阶为腹板根部的局部模态,且最低在第6阶就出现了局部模态。这是由于初步设计中,两腹板在靠近根部区域的铺层设置过薄,弯曲刚度过低,从而导致此区域腹板在相对较低的频段内即出现局部弯曲模态。根据上述分析,建议在叶片的后续设计中增加腹板在这一区域的厚度。此例说明:采用三维壳模型进行叶片结构分析有利于揭示叶片的薄弱部位,而采用梁模型则无法揭示叶片的这些细节特性。
3 静气弹稳定性分析
本文中考虑的静气弹稳定性分析主要是指定常气动载荷下的叶片结构屈曲分析。如前所述,大型风机复合材料叶片结构从整体上看近于复杂薄壳结构,因此在其结构设计中已由过去主要考虑疲劳破坏发展到目前必须同时考虑结构稳定性问题。关于风机叶片的屈曲,国内外已有部分工作[5-6]。然而,这些工作都是采用近似梁模型完成的。尽管也有个别研究人员曾用壳模型进行叶片屈曲分析[7],但是,其采用的叶片表面压力分布仅仅是一种人为假定的三角压力分布。随着CFD技术和计算机软硬件的不断发展,CFD技术被越来越多地应用于风机气动性能及载荷特性的预测[8]。与动量叶素理论等简化理论相比,CFD技术能够提供更多的细节,如更真实的叶片表面压力分布。本文将CFD计算所得叶片表面分布压力导算到叶片结构计算有限元模型上,并以此作为载荷进行叶片屈曲分析。
3.1 分布压力的导算
CFD计算提供的叶片表面分布压力结果文件中提供的信息一般是CFD计算中所使用的叶片表面网格结点的坐标及其压力值。CFD计算时对叶片表面进行离散所需的网格数一般比结构计算所需有限元网格数目要大得多。此外CFD计算过程中建立叶片的几何模型时一般只关注叶片表面的形状,因此只需要建立叶片表面的几何模型,与此相对,结构建模需要考虑叶片表面各区域不同的复合材料铺层以及腹板等内部结构。由于在建模上有上述不同的侧重点,风机叶片CFD计算和结构计算一般无法采用同一套网格进行。我们的解决方案是:分别建立各自的网格,首先进行CFD计算,完成后输出叶片表面网格上的分布压力,然后将流体网格上的压力导算到结构有限元模型上,最后进行结构计算。本文通过编制插值程序以实现上述压力导算过程,其流程如图4所示。
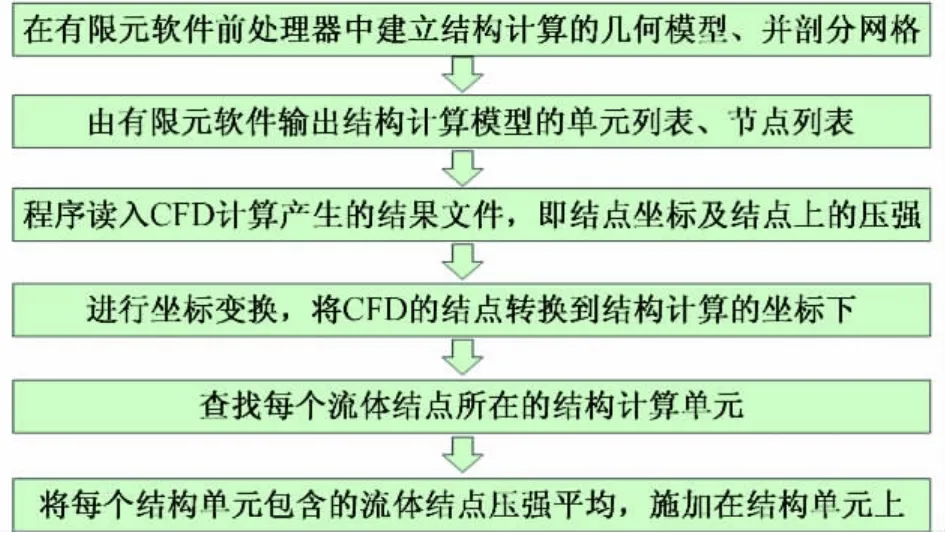
图4 分布压力导算过程示意图Fig.4 A flowchart of the pressure mapping procedure
针对本文所考虑的算例,采用六个典型风速下的分布压力进行屈曲分析,六个风速分别为6m/s、10.5m/s、13m/s、16m/s、19m/s 和 25m/s。采用上述压力导算程序分别将这个六个风速下CFD计算所得的叶片表面分布压力施加到叶片三维有限元壳模型上。图5以16m/s为例给出了该风速下导算到叶片结构模型上的分布压力图。

图5 叶片有限元模型上施加的分布压力(风速:16m/s)Fig.5 Pressure applied on the finite element model of the blade(wind speed:16m/s)
3.2 屈曲分析
采用前文中建立的复合材料壳模型,将上述六个风速下的分布压力导算到有限元模型后进行屈曲分析,分析中仍然考虑了离心力引起的应力刚化和旋转软化效应。计算所得上述六个风速下叶片的前四阶屈曲载荷因子列于表2中。
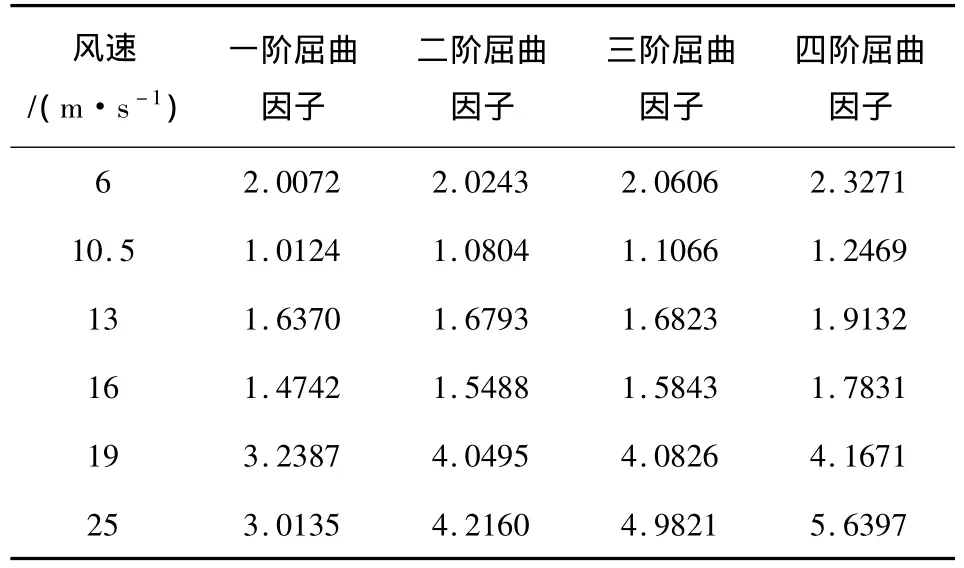
表2 某初步设计的1.5MW风机叶片屈曲载荷因子Table2 Load factors of first 4 buckling modes
从表2中可以看出,所分析风速下叶片屈曲载荷因子都大于1,因此叶片在所考虑的六个典型风速下不会发生屈曲。由于本风机采用变桨距控制方式,当风速增加时,叶片桨距角增大,叶片表面压力并不随着风速单调增加,因此各阶屈曲载荷因子也并不随着风速单调减小。从屈曲载荷因子来看,在所考虑的六个风速中10.5m/s和16m/s对应的等效载荷较大。
仔细检查叶片在这六个风速下可能的屈曲模态发现,这些模态都是发生于腹板根部的局部屈曲。图6以16m/s风速为例给出了该风速下叶片的前四阶屈曲模态,由于是腹板根部的局部屈曲,为了方便观察,图中只显示了腹板。六个典型风速下的屈曲模态都是腹板根部的局部屈曲,反映了腹板根部设计较为薄弱,模态分析中腹板根部局部振型过早出现也揭示了这个问题。
4 结论
本文发展了大型复合材料风机叶片三维壳模型的参数化建模技术以及基于壳模型的叶片模态分析技术与静气弹稳定性分析技术。
利用参数化建模技术,通过给定叶片外形、内部构造及复合材料铺层信息,可快速建立细致的有限元三维壳模型。采用三维壳模型进行叶片结构动态分析及静气弹稳定性分析的结果表明,近似梁模型无法揭示风机叶片结构的细节特性,采用壳模型进行分析有利于识别叶片结构的薄弱部位。
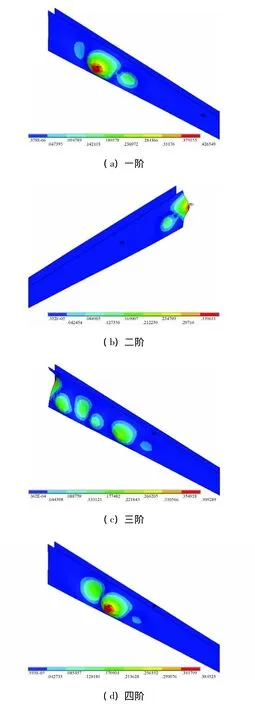
图6 叶片前四届屈曲模态(风速:16m/s)Fig.6 Buckling shapes of first 4 buckling modes(Wind speed:16m/s)
[1]刘雄,李钢强,李严,等.水平轴风力机叶片动态响应分析[J].机械工程学报,2010,46(12):128-141.
[2]廖猜猜,王建礼,石可重,等.风力机叶片截面刚度优化设计[J].工程热物理学报,2010,31(7):1127-1130.
[3]YIN J C,XIE Y,CHEN P.Modal analysis comparison of beam and shell models for composite blades[A].Asia-Pacific Power and Energy Engineering Conference[C].Wuhan,China,2009.
[4]LIU W,MA Y L,SU X Y,et al.Buckling analysis of wind turbine blade using pressure distributions obtained from CFD[A].Asia-Pacific Power and Energy Engineering Conference[C].Wuhan,China,2009.
[5]BIR G S,MIGLIORE P.Preliminary structural design of composite blades for two and three blade rotors[R].NREL/TP-500-31486.Golden,CO:National Renewable Energy Laboratory,2004.
[6]HERMANN T M,MAMARTHUPATTI D,LOCKE J E.Postbuckling analysis of a wind turbine blade substructure[J].Journal of Solar Energy Engineering-Transactions of the Asme,2005,127(4):544-552.
[7]MCKITTRICK L R,CAIMS D S,MANDELL J,COMBS D C,RABERN D A,VAN LUCHENE R D.Analysis of a composite blade design for the AOC 15/50 wind turbine using a finite elementmethod[R].SAND 2001-1441.Sandia National Laboratories,2001.
[8]LEISHMAN J G,GLENN L M.Challenges in modeling the unsteady aerodynamics of wind turbines[J].Wind Energy,2002,5(2):85-132.

