双下侧定几何二元混压式进气道的流场特征和气动性能分析
谢旅荣,郭荣伟
(南京航空航天大学能源与动力学院,江苏 南京 210016)
0 引言
超声速混压式进气道兼有外部压缩和内部压缩,它与外压式进气道相比外阻较小,而较内压式进气道易于起动,在飞行马赫数大于2.5时常被采用。二元进气道由于结构简单,易于制造,且可以根据不同的任务需求选择不同的布局形式,因此在一次性使用的吸气式超声速导弹中有较广泛的应用。进气道在导弹上的布局方式除了影响导弹的气动力特性外,对发动机特性尤其是进气道性能同样有着重要的影响[1-3]。但各种不同的布局方式均有优缺点,关键是要根据导弹的工作特点选择合适的布局。比如:欧盟的“流星”空空导弹选用双下侧布局,该布局方式便于机载,具有升阻比大、迎角性能好和横向空间较小的优点,但其侧滑性能较差[4];德国的“Armiger”反辐射导弹采用四个倒置二元进气道叉形布局,由于减小了隔道高度从而降低了整体阻力,而且进气道对称分布利于飞控,但该布局形式下的进气道其迎角/侧滑特性较差,升阻比小[5-6];法国的“ASMP”导弹采用的是两个二元进气道水平布局形式,进气道压缩面与弹身垂直,该布局形式的特点是升阻比高、迎角性能好,但其占用横向空间大。因此,对于二元进气道的气动特性研究需结合其布局形式进行分析。
本文结合双下侧布局形式对二元进气道的流场特征和气动性能开展了研究。国外,虽然已经有类似布局形式的导弹在研甚至已经试飞成功(如“流星”导弹),但是可能由于保密的原因鲜见相关文献报导。国内,对于定几何二元混压式进气道设计和数值仿真也进行了较多的研究[7-9],结合布局形式的研究主要针对叉形布局[10]和双下侧布局[11-13]。受到风洞试验条件的限制,结合双下侧布局形式获得的进气道性能参数主要是出口截面的。为了更深入的研究进气道通道内的流场特征和气动性能,本文在文献[4]基础上对其开展数值仿真研究,分析了双下侧布局形式的两个进气道在不同飞行状态下表现出的不同气动性能,并结合通道内的流场特征分析其原因。
1 数值模拟
1.1 物理模型
本文研究的二元混压式进气道为双下侧布局形式(如图1所示),工作马赫数范围是2.25~4.0,设计状态为马赫数Ma=3.0,迎角α=2°。具体型面参数请参见文献[4]。
1.2 数值方法
计算中用有限体积法求解雷诺平均后的三维N-S方程,紊流模型选用Jones和Launder提出的标准k-ε模型,采用一阶迎风格式离散。由于紊流模型只适用于离开壁面一定距离的紊流区域,而在与壁面相邻近的粘性边界层中,必须考虑分子粘性的影响,k-ε方程亦要作相应的修改,本文采用标准壁面函数。采用商业软件Fluent5.0计算,收敛准则为:连续方程、动量方程、能量方程以及k-ε方程的残差至少下降3个数量级,且进气道出口截面流量稳定。
采用结构化网格对整个计算域进行填充。由于研究对象几何形体十分复杂,整个计算域内被分为数十个子域进行网格生成,而后通过对接或耦合的方式形成一个整体。为了适合粘性计算以捕捉激波的需要,采用局部网格加密技术。由于在无侧滑、滚转下,计算对象结构对称、流场对称,为了节省计算网格单元,取1/2的流动区域进行网格划分,图1给出了该物理模型壁面网格图,计算网格数目约为56万。计算侧滑特性时采用全流动区域进行网格划分,网格数目约为84万。计算中采用的边界条件有:压力远场边界、压力出口边界、无滑移固壁边界和对称边界条件(1/2计算域时)等。

图1 二元进气道示意图Fig.1 Sketch of inlet and model

图2 壁面网格图Fig.2 Grids of the model
2 结果与分析
对物理模型进行数值仿真的工况范围为:来流马赫数 Ma=2.25~4.0,迎角 α =-6°~10°,侧滑角 β=0°~6°。研究范围内,来流的单位雷诺数大于1×107。实验是在南京航空航天大学NH-1风洞中进行的。NH-1风洞是暂冲式亚、跨、超声速风洞。试验段截面尺寸为(0.6m×0.6m)。超声速实验时通过更换喷管获得不同的来流马赫数。在试验马赫数范围内来流的单位雷诺数大于2×107。
下面首先给出数值仿真与试验结果对比验证,试验结果来自文献[4];然后分析数值仿真获得的进气道流场特征和气动性能。
2.1 计算和试验结果比较与分析
2.1.1 沿程静压分布曲线比较
图3给出了在设计状态下,计算和试验获得的进气道处于超临界状态和临界状态时唇罩面和压缩面沿程静压分布曲线。由图可见,计算获得的静压分布曲线和试验相当吻合。同时由图3的静压分布曲线也可以看出,在进气道出口截面稍上游处已经出现结尾激波系,这是由于气流拐弯段的影响造成的。图4给出了未加出口反压时不同纵剖面的计算马赫数分布图谱。可以看出在进气道对称面图谱的出口截面上存在结尾激波系。在试验中出口截面处为测量截面,受到总压测量耙的影响,试验得到的激波位置要比计算获得的位置前移。同时由图4拐弯段纵剖面的马赫数分布图谱可以看出,拐弯段内出现了局部亚声速区,但是被超声速区将其与下游隔离,因此反压必须提高到一定的值才能将进气道内已存在的结尾激波系往前推动。
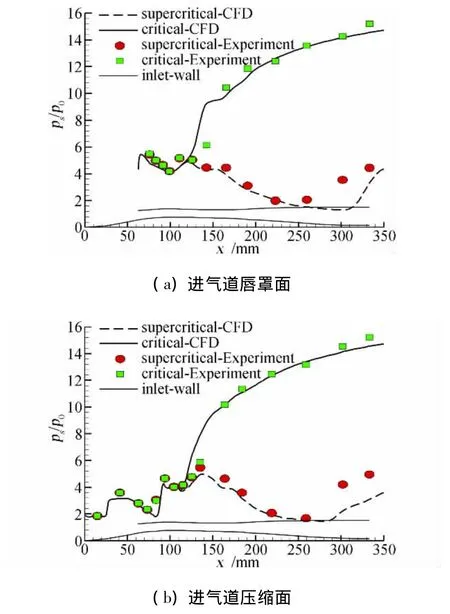
图3 Ma=3.0时进气道沿程静压分布曲线Fig.3 Distribution of static-pressure coefficient along duct at Ma=3.0

图4 Ma=3.0,α=2°,β =γ=0°超临界状态下进气道的马赫数等值分布图谱Fig.4 Mach number contours in the symmetry plane with supercritical operation at Ma=3.0,α=2°,and β =γ=0°
2.1.2 结尾激波系在超声速收缩通道内的流场特性
由文献[4]试验获得的进气道沿程静压分布曲线发现,当进气道结尾激波系位于喉道位置时,继续加大反压,结尾激波系可以稳定在收缩通道内。三维数值仿真获得了同样的结果。图5给出了Ma=2.5,α=2°,β=γ=0°下结尾激波系在收缩通道内和扩张通道内时计算和试验所获得的进气道沿程静压分布曲线,可见计算和试验结果变化规律一致。图6给出了对应于图5结尾激波系在收缩通道内时进气道对称面马赫数和流线分布图。可以看出,由唇罩面和压缩面上两道斜激波和弱激波串组成的结尾激波系,已不同于传统意义上混压式进气道的结尾正激波。根据数值仿真获得的流场参数由流量连续公式计算,发现在物理喉道前方的结尾激波系附近(图6.b所示的方框内)存在一个最小流通截面。这是因为当结尾激波系被推过喉道时,在面积收缩比较小的收敛通道后段,由于激波/附面层相互干扰形成了小于物理喉道的气动喉道。气动喉道的形成致使结尾激波系能“站立”在收缩通道内,保持稳定的工作状态。而且结尾激波系前马赫数减弱使进气道的性能高于临界状态时的数值。同样的情况在更高马赫数下也存在。数值仿真结果还发现,在Ma=2.25时结尾激波系不太容易在收缩通道内停留,这是因为物理喉道面积是按Ma=2.25确定的,尽管在设计时留有一定的裕度,但若形成比喉道还小的气动喉道时,易出现流量堵塞,从而将结尾激波系推出内通道,导致进气道不起动。
进气道在来流马赫数高于2.25时出现这种现象对于实际飞行是有利的,可以允许燃烧室压力在临界附近有一定范围的上下波动,而不影响到进气道捕获的流量和工作稳定性,有效提高了推进系统的稳定工作裕度。
综上所述,计算结果和风洞试验结果吻合良好,说明所采用的数值仿真方法可靠,结果可信,可作为该类进气道研究的有力工具。

图5 Ma=2.5不同反压下的沿程静压分布曲线Fig.5 Distribution of static-pressure coefficient along duct at different back-pressure ratios
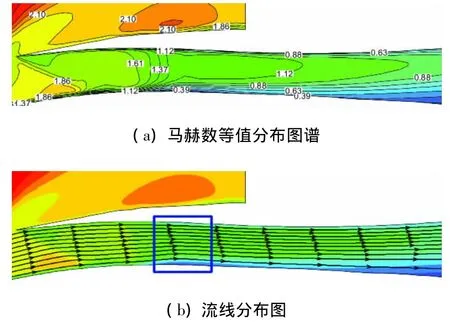
图6 Ma=2.5下结尾激波系在收缩通道内时进气道对称面马赫数等值和流线分布图Fig.6 Mach number contours and path lines in the symmetry plan when terminal shocks were moved in the convergent channels at Ma=2.5
2.2 进气道流场特征和气动性能分析
2.2.1 来流马赫数变化的影响
图7给出了α=2°,β=γ=0°时临界状态下进气道出口截面总压恢复系数和流量系数随来流马赫数的变化曲线。可以看出,计算和试验规律一致,随着来流马赫数的增加,进气道出口截面的总压恢复系数逐渐降低。在低于设计马赫数时,随着来流马赫数的增大,流量系数是升高的,到了设计马赫数3.0后流量系数变化不大,基本保持在1.0。图8分别给出了Ma=2.5和Ma=3.0,α =2°,β=γ =0°时临界状态下进气道对称面上的马赫数等值分布图谱。可以看出,Ma=2.5时斜激波波前马赫数和喉道马赫数相对于Ma=3.0时低,激波造成的总压损失相对较小,因此Ma=2.5时进气道的总压恢复系数高于Ma=3.0时的数值。同时由于Ma=2.5时进口前的斜激波角度相对Ma=3.0时大,存在较多的超声速溢流,导致流量系数低于Ma=3.0时的数值。
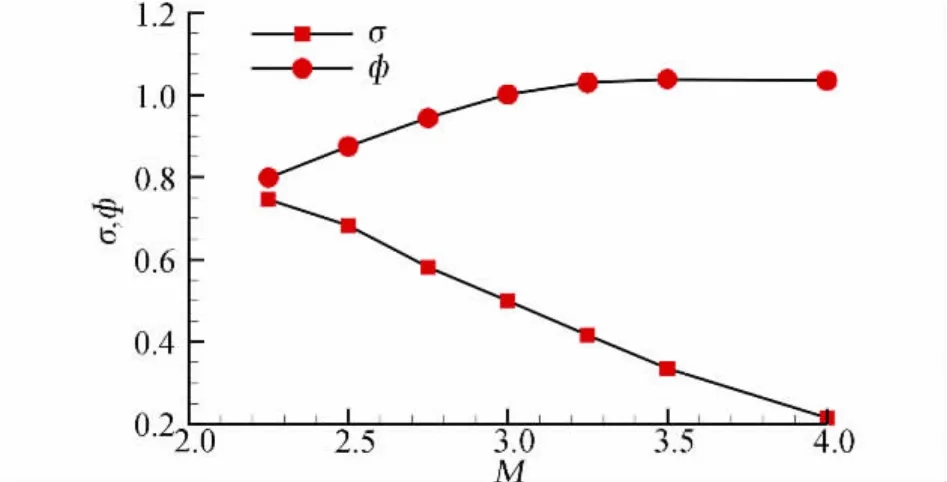
图7 α=2°,β=γ=0°时进气道总压恢复系数和流量系数随来流马赫数变化曲线Fig.7 Total pressure recovery coefficient and mass flow ratio vs flight Mach number

图8 临界状态时进气道对称面马赫数等值分布图谱Fig.8 Mach number contours in the symmetry plane
2.2.2 迎角变化的影响
图9给出了不同来流马赫数下进气道总压恢复系数和流量系数随迎角的变化曲线。可以看出,在研究范围内,随着迎角的增大,进气道的总压恢复系数和流量系数在来流马赫数为3.0和3.5时均是上升的。这说明双下侧布局方式的进气道迎角性能好。图10给出了Ma=3.0,β=γ=0°,α =2°和 α =8°时临界状态下进气道对称面的马赫数等值分布图谱。可看出,在α=8°时,进气道压缩面相对自由来流压缩角增大,波后马赫数降低,喉道马赫数相对于α=2°时降低较大,结尾激波系损失减小,因此总压恢复系数较高。
由图9还可以看出,在Ma=2.5,α从-2°增加到4°时总压恢复系数和流量系数是上升的。随着迎角的继续增大,总压恢复系数和流量系数下降后基本保持不变。图11给出了 Ma=2.5,α=6°,β=γ=0°时低反压下进气道对称面上的马赫数等值分布图谱。可以看出,进气道进口外唇罩出现一道类似弓形的激波,有亚声速溢流,因此Ma=2.5,α=6°时进气道总压恢复系数和流量系数均有所下降。图11还给出了该马赫数下α=10°时进气道对称面上的马赫数等值分布图谱,可以看出,与α=6°比较,α=10°时进口前的脱体激波更远离唇口,溢流更多。由图11还可发现,尽管进口前出现脱体激波,但是收缩段内的气动通道总能调整到使进气道的物理喉道加速到声速。也正是因为在研究的迎角范围内,进气道不起动后喉道总能达到声速,而喉道前的激波损失由于来流马赫数较低,总压损失变化不大,进气道的总压恢复系数基本不变,因此能通过喉道的流量基本不变,流量系数的变化也不大。同样的,在Ma=2.25,α =-4°~10°变化时,迎角增大到 2°后进气道性能也下降,随后基本保持不变,如图9所示。

图9 不同来流马赫数下进气道总压恢复系数和流量系数随迎角变化曲线Fig.9 Total pressure recovery coefficient and mass flow ratio vs angle of attack
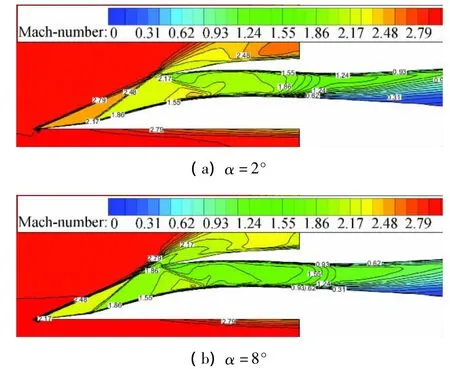
图10 Ma=3.0时不同迎角下进气道对称面马赫数等值分布图谱Fig.10 Mach number contours in the symmetry plane at different angles of attack at Ma=3.0

图11 Ma=2.5时不同大迎角下进气道对称面马赫数等值分布图谱Fig.11 Mach number contours in the symmetry plane at different angles of attack at Ma=2.5
2.2.3 侧滑角变化的影响
图12分别给出了Ma=3.0和Ma=2.5,α=2°,γ=0°时进气道总压恢复系数和流量系数随侧滑角的变化曲线。可以看出,在研究范围内Ma=3.0时,随着侧滑角的增加,两侧进气道的总压恢复系数均是下降的,但是迎风侧进气道相对于背风侧进气道的性能下降更大;同时,随着侧滑角的增加,背风侧进气道的流量系数是增加的,而迎风侧进气道的流量系数下降较厉害。图13 给出了 Ma=3.0,α =2°,β =4°,γ =0°时迎风侧处于临界状态下的两侧进气道对称面的马赫数等值分布图谱。可以看出,在迎风侧进气道处于临界状态时,背风侧进气道仍远离喉道位置处在超临界状态,两侧进气道结尾激波系位置存在差别。而且由于背风侧进气道压缩面相对来流压缩角度增大,波后马赫数较低,使进气道结尾激波系强度相对弱,因此背风侧进气道的总压恢复系数高于迎风侧进气道的。在研究的范围内,随着侧滑角的增大,背风侧进气道虽然受弹身的影响增大,但是由于进气道进口捕获面积增大,因此其流量系数是增大的,而迎风侧正好相反,所以两个进气道的流量系数变化趋势相反。

图12 进气道总压恢复系数和流量系数随侧滑角变化曲线Fig.12 Total pressure recovery coefficient and mass flow ratio vs yaw angle
图12给出的Ma=2.5时两侧进气道性能的变化曲线与Ma=3.0的规律不太一致,背风侧进气道的性能并未优于迎风侧的性能。这是由于在Ma=2.5,β=2°时背风侧进气道出现流量堵塞导致不起动,进口前增加了一道弓形激波,如图14所示,因此总压恢复系数和流量系数下降较大。随着侧滑角继续增大,背风侧进气道受到弹身的影响增大,进口前的总压损失较大,而受到迎风侧进气道承受反压能力的限制,结尾激波系更远离喉道致使总压恢复系数也随着下降。也正是由于喉道前的损失增大,进气道不起动后尽管喉道仍能达到声速,但其截面流通能力下降,从而使流量系数也随之下降。
3 结论
由以上分析得到如下结论:
(1)当来流马赫数高于起动马赫数2.25时,进气道处于临界状态下,出口反压继续增大,在一定范围内,结尾激波系可以停留在收缩通道内。

图13 Ma=3.0,α=2°,β =4°,γ=0°时临界状态下两侧进气道对称面马赫数等值分布图谱Fig.13 Mach number contours in the symmetry planeof the inlets at Ma=3.0,α=2°,β =4°,γ=0°

图14 Ma=2.5,α=2°,β =2°,γ=0°时超临界状态下两侧进气道对称面马赫数等值分布图谱Fig.14 Mach number contours in the symmetry plane of the inlets at Ma=2.5,α =2°,β =2°,γ=0°
(2)随着来流马赫数的增加,进气道斜激波损失和结尾激波损失增大,导致进气道的总压恢复系数随之下降。而流量系数随着来流马赫数的增大而增大,到设计马赫数及以上基本保持为1.0。
(3)一定范围内随着迎角的增加进气道的总压恢复系数和流量系数均是提高的;但在低马赫数大迎角情况下,进气道易出现不起动现象;当进气道出现不起动时,进气道的总压恢复系数下降;继续增大迎角,其总压恢复系数和流量系数基本保持不变。
(4)由于共用同一燃烧室,在侧滑情况下,背风侧进气道受迎风侧进气道承受反压能力下降的限制,两侧进气道的性能均下降。随着侧滑角的增大,迎风侧进气道的流量系数逐渐降低,背风侧进气道则是增大。当低马赫数大侧滑角下进气道不起动时,其总压恢复系数和流量系数均下降。
(5)通过与风洞试验结果比较,表明所采用的数值方法是可信的,可作为该类进气道研究的有力工具。
[1]CLYDE H.Aerodynamic characteristics of a series of twin-inlet air-breathing missile configurations(Ⅱtwo-dimensional inlets at supersonic speeds)[R].NASA TM-84559,1983.
[2]谢旅荣,郭荣伟.双下侧布局二元超声速进气道掺混气动特性[J].航空学报,2007,28(6)∶1287-1295.
[3]李博,梁德旺.混压式进气道与弹体一体化流场数值模拟[J]. 推进技术,2002,23(4)∶307-310.
[4]谢旅荣,郭荣伟.双下侧定几何二元混压式超声速进气道的风洞试验[J].航空学报,2009,30(6)∶1000-1006.
[5]万大为,郭荣伟.定几何二元倒置“X”型混压式超声速进气道实验[J].南京航空航天大学学报,2007,39(3)∶277-281.
[6]WAN D W,GUO R W.Experimental investigation of a fixed-geometry two geometry two dimensional mixed-compression supersonic inlet with sweepforward high-light and bleed slot in a"X"-type layout[J].Chinese Journal of Aeronautics,2007,20(4)∶304-312.
[7]王国辉,李进贤,蔡体敏.二元混压超声速进气道三维流动数值分析[J].推进技术,2001,22(2)∶118-121.
[8]洛广琦,郑九州,宋頔源.考虑附面层影响的二元混压式进气道设计[J].航空动力学报,2009,24(9)∶2063-2068.
[9]刘晓伟,何国强,秦飞.宽马赫数固冲二元进气道设计与研究[J].宇航学报,2008,29(5)∶1577-1582.
[10]鲍福廷,李进贤,赵飞.固冲发动机双下侧二元进气道设计研究[J]. 西北工业大学学报,2002,20(4)∶590-593.
[11]白鹏,朱守梅,孟宇鹏,等.冲压发动机进气道和掺混段节流特性数值研究[J].推进技术,2004,25(6)∶503-507.
[12]谢旅荣,郭荣伟.一种定几何混压式二元进气道的再起动特性研究[J].航空动力学报,2007,23(2)∶590-593.
[13]麻肖妃,谢旅荣,郭荣伟.双下侧布局带泄流腔二元进气道试验[J].航空动力学报,2010,25(8)∶1818-1824.

