三维非结构自适应多重网格技术

许和勇，叶正寅

(西北工业大学翼型叶栅空气动力学国防科技重点实验室，陕西 西安 710072)

0 引言

非结构网格舍去了网格节点的结构性限制，易于控制网格单元的大小、形状及网格点位置，对复杂外形具有很强的适应能力，这使得非结构网格技术在20世纪80年代末和90年代初得到了迅速的发展［1］。非结构网格中的一个点周围的点数和单元数是不固定的，所以可以方便地进行自适应加密，以提高计算的精度，文献［2-6］对非结构网格的自适应算法进行了较深入的研究。为了使得加密后的网格能够反映真实的边界形状，文献［2-3，6］采用的方法一般都是输入边界的表面函数方法，如果边界形状比较复杂，则形成一个表面函数来表示边界是比较麻烦的，所以本文发展了一种较为简易、容易操作的基于边界外形的自适应方法，通过生成一套初始极密表面网格来使得加密后的网格保持边界的原始几何形状。

另外，非结构网格节点和单元的无序性也导致了网格参数的存储信息量增加，计算的速度下降，所以提高非结构网格的计算效率也成了近些年来的研究热点。采用多重网格方法是CFD计算中提高计算效率的重要措施之一，它可以大大减少计算机时。基于结构网格的多重网格技术目前发展得已经非常成熟［7-8］，而基于非结构网格的多重网格方法则仅有少量的国内外文献［9-11］发表。本文将自适应后的网格作为多重网格，然后采用多重网格算法，以提高计算速度。

1 控制方程

采用三维Euler方程作为控制方程，其守恒型积分形式为:

对于理想气体有:

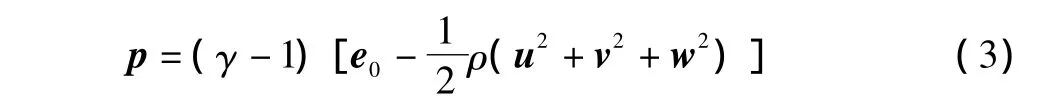
2 基于几何外形的自适应网格技术

自适应网格加密的一般步骤为:

(1)计算得到粗网格上的流场解;

(2)根据选定的自适应判据，对满足细分条件的网格边作细分标志，即在该边中点增加一个网格点;

(3)检查所有的三角形面，要求每一个三角形的三条边只允许有一条边加点，或一个面的三条边都加点，如图1所示;

(4)检查所有的四面体单元，要求每一个四面体单元的六条边只允许有一条边或同一个三角面的三条边或六条边都加点，如图2所示;

(5)对于边界上的加密边，要保证其加密点落在边界上;

(6)计算细网格上的流场解;

(7)返回步骤2。

图1 三角形面剖分的两种情况Fig.1 Two cases of face division

图2 四面体剖分的三种形式Fig.2 Three cases of tetrahedron division

流场内部的网格单元边可以按照图1和图2的剖分方法直接进行加密点的添加，但是处于边界上的单元边在添加加密点时，如果直接取边的中点，则会出现如图3(a)所示的情况，无法使得边界的原始形状得到保持。所以，网格自适应应该是基于初始几何外形的自适应，所要添加的点要添加到初始几何外形上而不是添加到已有的网格边上，如图3(b)所示。

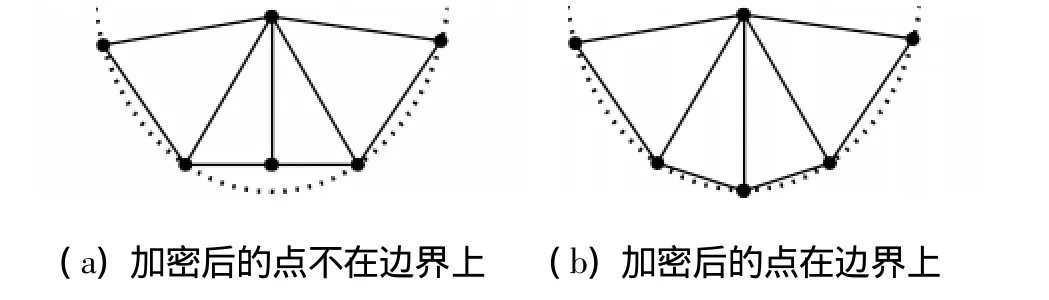
图3 边界点加密示意图Fig.3 Sketch map of boundary refinement

为了使得加密后的边界点能够落在边界上，本文提出了一种简单易行的方法，通过预先生成的一套初始极密表面网格来将边界网格加密点近似投影到边界上，具体步骤如下:

(a)在进行网格自适应求解之前，对整个边界生成一套极密的表面网格，作为原始边界的近似描述，如图4，为了观察方便，某机翼端面的网格已隐去，只保留翼型边界上的点，即没有编号的较小点;

(b)对初始的粗网格进行自适应剖分，初步确定所有的加密点，如图4中的点A、B、C、D、E等即为端面粗网格的边界节点;

(c)找出粗网格上所有边界加密点(例如图4中的点P、Q)，然后将点投影到密网格上，从密网格的三角形单元中插值确定修正后的加密点坐标，作为新的加密点坐标。例如，将点P沿着线段AB的中垂线方向投影，与密网格的边界边P1P2相交于点P'，则P'即为点P的新位置，对于点Q同理，如图5所示。

这样就将边界加密点从网格边的中点挪动到了边界上了，使得自适应加密后的边界保真性较好，从而提高了最终的流场计算精度。

图4 初始极密表面网格与粗网格边界示意图Fig.4 Sketch map of the initial boundaries

图5 边界加密点向边界上投影后的效果图Fig.5 Sketch map of the boundaries after refinement

3 多重网格技术

多重网格算法需要有不同单元数目的多套网格，形成这些网格的方法主要有单独生成［12］以及从最密网格聚合生成［13］两种方法。单独生成的多重网格在计算时的插值关系需要查找确定，具有一定的计算量，而且存在数据传递的精度问题;聚合法需要预先从初始密网格不断聚合生成，聚合后的粗网格单元不规则性太大，对计算收敛性有一定影响。而本文利用自适应后的网格作为多重网格，不但粗细网格之间的对应关系很容易确定，而且每一层网格的质量较好。

3.1 多重网格的确立

本文的多重网格建立的步骤为:在进行自适应加密过程中，对每一层的网格作标记，例如记初始的粗网格为第一层，第一次加密后形成的网格为第二层，直至得到第n层网格，同时记录第1层与第2层，…，第n-1层与第n层的网格单元之间的对应和包含关系。这样多重网格计算所需要的网格单元对应和包含关系就确定了，示意图如图6所示。

图6 不同层的多重网格示意图Fig.6 Sketch map of three multigrid levels

3.2 多重网格的算法

时间推进中，在细网格上的计算格式为:

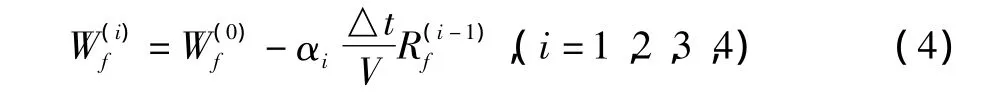
其中αi为常系数，Rf为残值量，V为单元体积，Wf为守恒变量。

在较粗网格上的计算格式为:

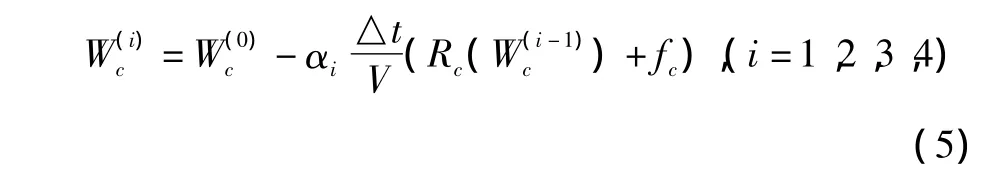
守恒变量Wf和残值Rf由细网格插值到较粗网格上的公式为:

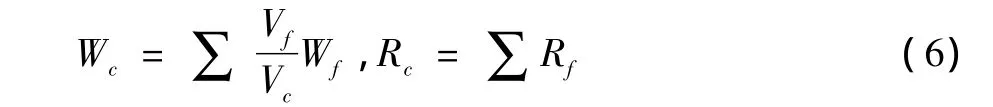
其中下标c表示粗网格量，f表示细网格量，Vf和Vc分别表示细网格和粗网格的单元体积。求和是对粗网格中包含的所有细网格进行。

粗网格的修正量向细网格传输时，细网格的修正量近似等于细网格所在粗网格的修正量。

4 算例

以M6机翼的跨声速绕流计算作为算例，计算的来流马赫数为0.8395，迎角为3.06°。图7(a)给出的是初始粗网格的机翼表面网格，图7(b)为边界加密时要用到的表面极密网格放大图。网格边的加密条件是两个节点的密度值的差大于计算域平均值的1.3倍。第一次自适应加密后得到第二套较密网格，然后应用多重网格算法得到第二套网格上的流场解，再进行自适应加密得到第三套网格，如此执行，直至得到第四套网格，并用多重网格方法计算得到流场解。各套网格的数据如表1所示。

图7 M6机翼的表面粗网格和极密网格图Fig.7 Coarse grid and fine grid of the M6 wing surface

表1 M6机翼自适应多重网格情况Table1 The adaptive multigrids for M6 wing calculation

图8给出的是三次自适应后第四套网格的表面网格图，可以看出表面的“λ”形激波被捕捉得非常清晰。图9中虚线表示在计算最后一次流场解时不使用多重网格的残值收敛情况，而实线表示采用四重网格求解时的残值收敛情况，横坐标表示CPU时间，可见对于本算例来说，多重网格的加速比达到5.3左右，大大缩短了计算时间。

图8 自适应后的机翼表面网格Fig.8 Surface grid after refinement

图9 多重网格残值收敛比较图Fig.9 The comparison of the calculation residual

图10给出的是机翼展向65%和90%处的表面压力系数分布曲线图。图中虚线表示原始粗网格计算所得到的结果，而实线表示采用本文所发展的自适应方法后得到的结果。通过和实验数据的比较可以看出，虚线与实验结果相差较大，主要是因为机翼前缘的加密点没有投影到机翼表面上，使得机翼前缘形状“失真”，所以导致压力极值点后移，且峰值偏低;而采用了本文的基于几何外形的自适应技术后，机翼表面上网格边加密点落在机翼的表面上，保持了机翼的原始形状，计算结果与实验值更加吻合。

5 结论

本文发展了一种基于几何外形的非结构自适应多重网格求解技术，对初始的粗网格根据加密判据进行剖分，得到与流场结构相一致的较密网格，从而可以用较少的网格数来达到较高的求解精度。在进行网格自适应时，通过预先生成的初始极密表面网格来将表面网格边上的加密点投影到边界上，使得加密后的网格保持了边界的初始外形。将自适应加密后得到的各层网格作为多重网格，采用多重网格算法进行流场求解，提高了计算效率。M6机翼的算例表明，本文所发展的方法比较准确地捕捉到流场中的激波，而且机翼表面的压力系数分布与实验值更加吻合。

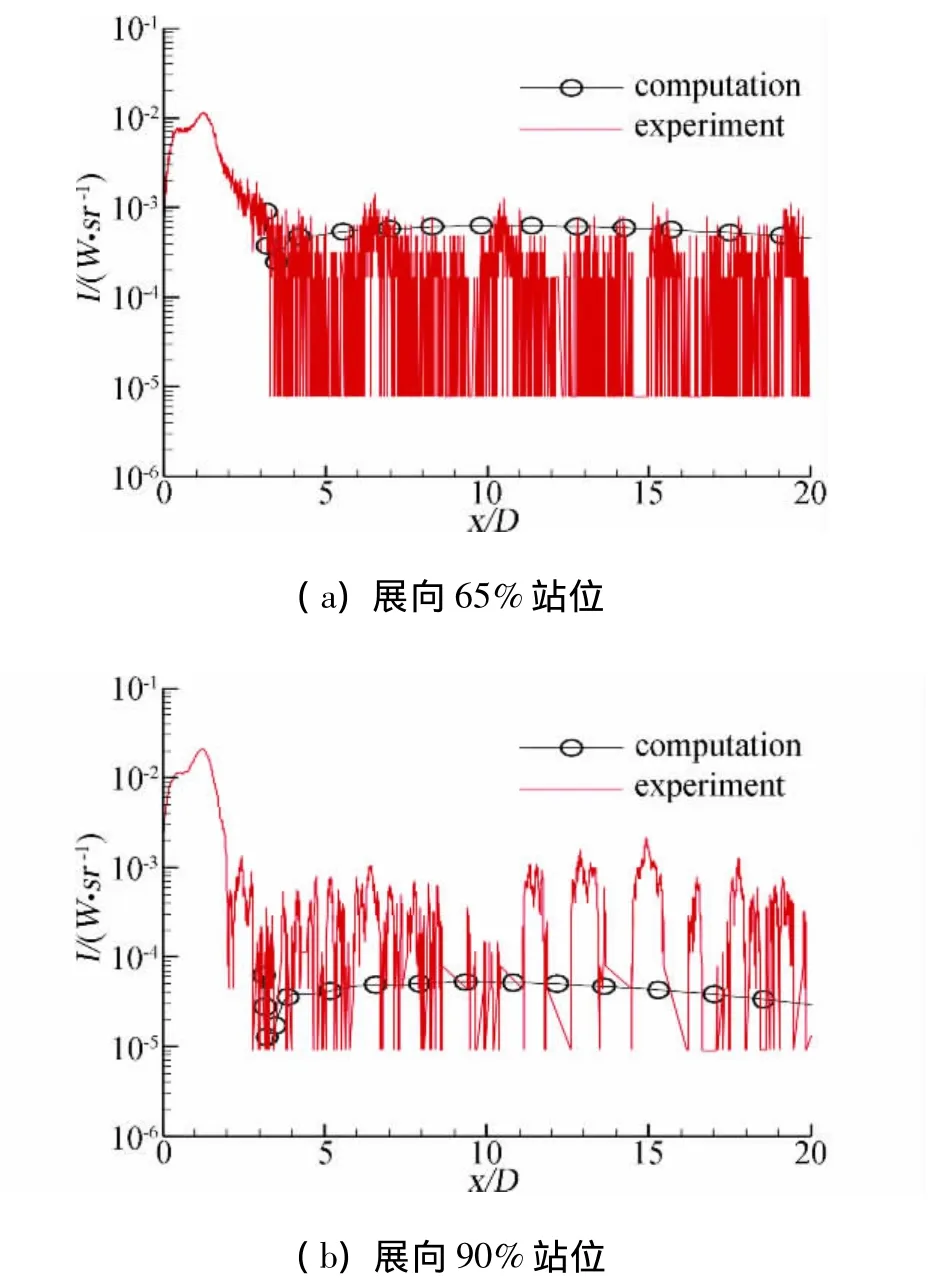
图10 机翼展向位置的表面压力系数分布曲线Fig.10 Pressure coefficient distributions at different locations on the wing surface

［1］朱自强.应用计算流体力学［M］.北京:北京航空航天大学出版社，1998.

［2］CONNELL S D，HOLMES D G.A 3D unstructured adaptive multi-grid scheme for the Euler equations［R］.AIAA 1993-3339-CP，1993.

［3］HOLMES D G，CONNELL S D.Solution of the 2D Navier-Stokes equations on unstructured adaptive grids［R］.AIAA 89-1932，1989.

［4］王平，朱自强，拓双芬，等.三维自适应非结构网格的Euler方程解［J］. 航空学报，2001，22(6):495-499.

［5］朱培烨.三维Euler方程的自适应非结构网格计算［J］.航空计算技术，2002，32(4):23-26.

［6］邱征，周磊，朱培烨.三维Euler方程非结构自适应网格投影和光顺技术研究［J］.航空计算技术，2006，36(1):79-85.

［7］SWANSON R C，TURKEL E.Multistage schemes with multi-grid for Euler and Navier-Stokes equations［R］.NASA TP-3631，1997.

［8］杨爱明，翁培奋，乔志德.用多重网格方法计算旋翼跨声速无粘流场［J］.空气动力学学报，2004，22(3):313-318.

［9］吕宏强，伍贻兆，夏健.非结构聚合多重网格法流场数值模拟研究［J］.航空学报，2002，23(1):74-79.

［10］朱培烨.三维非结构网格的欧拉方程聚合多重网格法［J］. 航空计算技术，2004，34(3):6-9.

［11］MOHAGNA J P，NEAL T F.Agglomeration multi-grid for unstructured grid flow solver［R］.AIAA 2004-759，2004.

［12］MAVRIPLIS D J.Three dimensional unstructured multigrid for the Euler equations［J］.AIAA Journal，1992，30(7):1753-1761.

［13］VENKATAKRISHNAN V，MAVRIPLIS D J.Agglomeration multigrid for the three dimensional Euler equations［R］.ICASE Report 94-5.Hampton，Virginia:NASA Langley Research Center，1994.