考虑气动弹性的风力机叶片性能分析

陈佳慧，王同光

(南京航空航天大学江苏省风力机设计高技术研究重点实验室，江苏 南京 210016)

0 引言

随着风力机朝着大尺寸、大挠度的方向发展，叶片的气动弹性问题日益引起关注。目前国内外已有的风力机叶片气动设计方法和软件大都是假设叶片为刚性体，即在不考虑叶片弹性变形的前提下，通过改变叶片的翼型、弦长和扭转角沿展向的分布来设计满足一定气动特性要求的叶片外形。然而，由于真实叶片并不是刚性的，在实际的运转状态下，必然产生弹性变形。对于大型风力机叶片，由于设计功率成倍增加，所受载荷大幅提高，受制于重量与体积，结构更为细长。刚度降低会产生较大的弯曲和扭转变形，导致叶片在实际运转中气动外形与设计外形产生偏差，使叶片偏离原设计点，影响气动效率，并对风力机正常运转造成较大的影响［1-2］。因此，研究气动弹性对叶片以及风力机组的影响，并将其应用于叶片设计与优化，对提高叶片气动性能、气动设计准确性和结构安全性，有重要意义。

本文将气动弹性影响引入风力机叶片的气动计算中，对一大型变桨型风力机进行了多种风速下叶片载荷及风轮性能等计算，并与刚性假设下的原计算结果进行对比，分析了气动弹性对叶片气动外形的改变，以及气动弹性对风轮性能的影响;并对气动弹性引起载荷重新分布的情况进行了计算，分析了其对结构设计的影响。

1 方法描述

静气动弹性分析分别需要用气动和结构分析方法来计算载荷与变形，由于叶片在气动设计阶段需要进行多种工况下的运算，在保证精度的前提下应以快速运算和多轮优化为主要目标，因此本文选用计算效率高、结果可靠的带修正BEM理论和盒形梁理论分别计算稳态载荷和结构变形，耦合静气动弹性平衡方程，进行求解。

1.1 气动分析方法

叶素动量理论(BEM理论)［3］是用于风力机性能分析最为简便快捷的方法。不仅广泛用于风力机的设计和性能计算，而且还用于计算风力机的载荷。同时BEM理论还不断地被进一步改进［4-5］，以提高计算准确性，扩大适用范围。

本文以BEM理论为基础，引入叶根损失和叶尖损失［4］，并在轴向诱导因子a较大时使用Ct的经验模型。使用该方法，可以计算在不同风速、转速和桨距角配置下的稳态载荷以及功率。

1.2 结构分析方法

风力机叶片属于梁式多闭室薄壁结构，本文采用盒形梁理论［6］来分析结构内力分布，再求出静气动弹性分析时所需的扭转角。由于外载荷与结构均沿展向变化，因此进行结构分析时可先用片条理论将叶片离散，离散位置与气动分析时一致，然后对每一片条进行求解。

叶片弦向刚度比展向刚度要大得多，可以假设叶片的翼剖面没有弦向变形［8］;由于每一剖面外形与材料分布均不同，而结构形式基本一致，故先沿弦向将剖面离散成若干微段，再进行数值积分求得截面特性。多闭室结构为静不定结构，求解时需切开闭室，形成开剖面系统，以解除静不定。使用式(1)计算开剖面剪流:

式中 Qx、Qy分别为剪力，Jx、Jy、Sx、Sy分别为剖面上承受正应力的面积对x轴和y轴的惯性矩和静矩。

利用力矩平衡条件∑M=0和变形协调条件θ=θi，求出平衡剪流q0i，与开剖面剪流～q相加得到盒形梁剖面的最终剪流qi，再根据卡氏定理，使用式(2)求解相对扭角 θ［7］。

式中Ai为各闭室周线所围面积，∮i表示沿各闭室周线积分，G表示材料的剪切弹性模量，t表示壁板的厚度。求得各剖面相对扭角后，可沿展向进行积分，得到各剖面绝对扭角的展向分布。

利用盒形梁理论，可先求出弯心位置，将剪力平移到弯心上，等效为力与力矩，再与气动附加力矩叠加，即得到气动力对弯心的总力矩，求解扭角时可只作用力矩以简化计算。可先后作用一剪力Q和扭矩Mz于翼剖面上，分别求出引起的相对扭角θq和θm，再根据式(3)可得到弯心相对剪力作用点位置。

设计时将各翼剖面弯心布置在一条直线上，该直线即为弹性轴。

1.3 静气动弹性的耦合计算

叶片在气动设计阶段只计算运行时的稳态载荷，结构的弹性变形被认为是缓慢发生的，由变形速度和加速度引起的空气动力与弹性力相比，可以忽略不计，时间不以独立的变量出现在气动弹性平衡方程中［8］。

由于叶片的翼剖面几何扭转角变化即为攻角增量αe，对叶片气动载荷的影响比其他方向弹性变形的影响都大得多，因此本文在气动弹性变形计算中只考虑了叶片沿展向的翼剖面几何扭转角的变化［9］。

典型翼型剖面的气动弹性的静平衡方程式［10］为:

式中L为升力，e为从气动力中心至弹性轴的距离，MAC为绕气动力中心的力矩，Kα为弹性弹簧常数。

风力机叶片工作在大攻角下的状态较多，阻力分量引起的扭矩不可忽略;而针对多闭室结构的求解方法，式(4)右侧的弹性力矩项也必须作出相应修改，因此得到以下的气动弹性静平衡方程式:

式中D为阻力，αe为攻角增量。式左边为气动力对弯心的扭矩，右边为结构内部剪流引起的扭矩。

本文首先使用改进的BEM理论得到叶片的气动载荷，进行相应的坐标变换后使用盒形梁理论计算叶片各剖面的扭转变形，计及变形后的叶片重新计算气动力进行下一轮迭代，如此循环直到气动载荷变化与结构弹性变形均满足收敛条件，即所谓的静气动弹性平衡状态。单个工况的静气动弹性计算流程如图1所示。

图1 单个工况的静气动弹性计算流程图Fig.1 Theflowchartofstaticaeroelasticcalculation insingleworkingstatus

2 算例与结果分析

2.1 计算模型

本文采用一大型变桨型风力机叶片及风力机运行控制律作为计算模型。该模型先期在不考虑气动弹性影响的情况下已进行了设计。风力机额定功率、额定转速等参数已给定，叶片长度、弦长、扭角、厚度、翼型等气动参数以气动性能为目标，都已进行了设计和优化。考虑风力机从切入风速到切出风速的整个运行过程，制定了控制曲线，如图2、图3所示，分为3个阶段:

1)低风速阶段:切入后，转速恒定，尖速比逐渐减小，功率系数Cp逐渐增大到最大值。

2)跟踪功率系数最大值阶段:在5m/s～10m/s风速范围内，随着风速增大，通过改变转速使功率系数始终为最大，直到达到额定功率。

3)额定功率阶段:转速恒定，通过改变桨距角使输出功率始终为额定功率，直到达到切出风速。

图2 刚性假设下的桨距角控制曲线Fig.2 Pitchanglecontrolcurveunderrigidsupposition

图3 转速控制曲线Fig.3 Therotatingspeedcontrolcurve

在此模型基础上，本文引入气动弹性，对风轮性能，叶片载荷等进行计算，并分析其影响。

2.2 气动弹性对叶片的影响

本文首先计算了典型风速下叶片受气动载荷后的弹性变形情况。图4显示了叶片扭转角刚性假设下的设计值与计及叶片弹性变形后的扭转角计算值的比较，风力机翼型约定低头为正，由图可见叶片在气动载荷作用下发生了明显扭转，且越靠近叶尖的部分扭转角逐渐增大，而该部分对发电量的贡献也最大，弹性变形对叶片气动性能将产生明显影响。

对比图5中的曲线与图2、图3所示的控制曲线可以看出，叶根扭矩随着风速的变化规律受到转速与桨距角改变的影响，曲线前两个拐点分别对应转速在固定与变化之间的切换，第三个拐点对应由固定桨距角切换到变桨状态。叶根扭矩表征了叶片总体受载的情况，叶尖受载荷后的扭角变化规律与扭矩的变化规律相一致。总体而言，气动弹性对叶片气动外形的影响随着风速的增大而增大，风轮性能也将随之改变。

图4 叶剖面扭转角沿展向分布比较Fig.4 Comparisonoftwistdistributions ofbladeprofiles

图5 叶根扭矩与叶尖扭转变形随风速变化曲线Fig.5 Windspeed-torqueofrootandwind speed-torsionaldeformationofbladetipcurves

2.3 气动弹性对风轮性能的影响

功率系数Cp是功率P的无量纲化，体现了风能利用率。本文以功率系数表征风轮性能，计算了Cp随风速和叶尖速比的变化情况，以分析不同工况下气动弹性对风轮性能的影响。为便于比较，刚性假设与弹性假设的工况参数均相同。

图6比较了考虑气动弹性影响前后Cp随风速的变化曲线，由图中可以看出，从切入风速至5m/s风速的低风速区，气动弹性对Cp有一定正的影响，但由于气动载荷较小，叶片弹性变形较小，因此对Cp影响不大;从5m/s至10m/s风速附近的区域，气动弹性对Cp的影响很小;在大于10m/s风速的区域，风轮达到额定功率，由于机组功率的限制，叶片进入变桨控制阶段，此时Cp值下降。随着风速的增大，叶片所受载荷使结构产生弹性变形，气动外形的变化量随之增大，两条曲线表示的Cp值差异明显增大。因此在大风速区域，气动弹性将对风轮的性能产生明显影响。

图7对Cp随叶尖速比λ的变化进行了比较，从图中可以看出，在λ小于7的区域，气动弹性计算的Cp低于刚性假设下计算的Cp，表明气动弹性对风轮性能产生负面影响;λ从7至10附近的区域两曲线Cp差值很小，表明气动弹性对Cp最大值影响很小;随着λ继续增大，气动弹性计算的Cp逐渐高于刚性假设下计算的Cp，此区域对应图6中的低风速区，对风轮性能影响不大。

图6 考虑气弹前后Cp随风速变化的比较Fig.6 Comparisonofwindspeed-Cpcurve with/withoutaeroelasticeffect

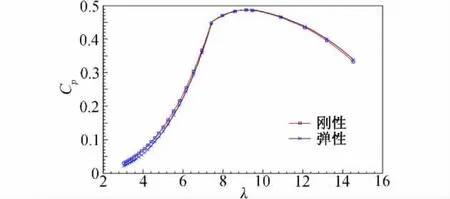
图7 考虑气弹前后Cp随λ变化的比较Fig.7 Comparison ofλ-Cpcurvewith/without aeroelasticeffect

2.4 气动弹性对载荷分布及结构设计的影响

功率系数Cp对风轮设计具有重要意义，而对风力机整个设计过程而言，需要考虑各方面的因素。叶片载荷是结构设计的主要输入条件，本文对叶片载荷较大的工况进行了气动弹性影响的分析。

如2.1节计算模型中所述，风力机在达到额定功率后转速恒定，通过改变桨距角使输出功率保持额定功率，直到达到切出风速。在进行气动弹性计算后发现，与刚性假设下得到的桨距角控制曲线相比，弹性叶片保持额定功率所需的桨距角值更小。随着风速继续增大，两种计算结果的差异逐渐扩大，如图8曲线所示。主要原因在于原设计通过增大桨距角(低头)来减小攻角，从而保持功率不变，但由于气动载荷增量产生了附加低头力矩，使叶片结构发生扭转变形，实际攻角比刚性假设下的值更小，因此在考虑弹性变形时，所需的桨距角更小。

由于叶片气动外形已发生变化，即使在考虑气动弹性的情况下风力机达到了目标功率曲线，叶片上的载荷分布也与刚性假设下设计考虑的载荷分布不同。图9比较了同一风速下刚性和弹性叶片的剪力图，从图中可以看到，靠近叶根部分和60%至80% 展长的部分，刚性叶片和弹性叶片沿展向的剪力分布有较大差别，刚性假设计算所得的载荷偏小，二者最危险截面的载荷相差接近50%。如果采用刚性假设计算的载荷来进行结构设计，误差将增大，叶片结构将偏危险。因此，忽略气动弹性影响将对叶片结构设计的安全性构成影响。从另一方面来看，气动弹性计算所得的载荷及分布更为准确，采用计及气动弹性影响的载荷能够更精确地进行结构设计。

图8 考虑气弹前后的变桨控制曲线比较Fig.8 Comparison of pitch angle control curveswith/without aeroelastic effect

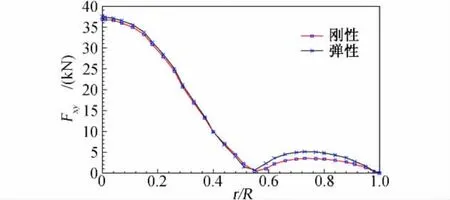
图9 考虑气弹前后的叶片最大剪力图比较Fig.9 Comparison of the maximum shearing forcesof blade with/without aeroelastic effect

3 结 论

通过对计算结果的分析可以得到以下结论:对于兆瓦级风力机，随着风速和载荷的增加，叶片的弹性变形逐渐增大，气动外形将发生明显改变，从而影响到风轮性能。气动弹性对Cp最大值影响不大，但对大风速大载荷区域的风轮性能将产生明显的影响。叶片载荷由于气动弹性的作用将发生改变，从而影响到原结构设计的准确性。本文的方法在气动和结构计算模型足够准确的条件下，能较好的计算气动弹性对风轮性能及叶片载荷的影响，用于对叶片气动设计与载荷计算方法进行修正，以更好的进行叶片设计。

［1］RASMUSSEN F ，et al.Present status of aeroelasticity of wind turbines［J］.Wind Energy，2003，6:213-228.

［2］HANSEN M O L，et al.State of the art in wind turbine aerodynamics and aeroelasticity［J］.Progress in Aerospace Sciences，2006，42:285-330.

［3］GLAUERT H.Airplane propellers［M］.Aerodynamic theory.New York:Dover Publications，1963.

［4］SHEN W Z，et al.Tip loss corrections for wind turbine computations［J］.Wind Energy，2005，8(4):457-475.

［5］WILSON R E，HARMAN C R.Tangential induction and its effect on wind turbine performance and loads［J］.ASME Journal of Solar Energy Eng.，117(2):157-158，1995.

［6］SAMSON D R.The analysis of shear distribution for multi-cell beams in flexure by means of successive numerical approximations［J］. Journal of the Royal Aeronautical Society，1954.

［7］CHUN M，NIU Y. Airframe stress analysis and sizing［M］.Hong Kong:Conmilit Press，1999.

［8］FöRSCHING H W.Grundlagen der aeroelastik［M］.New York Berlin Heidelberg:1974.

［9］詹浩，华俊，张仲寅.考虑气动弹性变形影响的跨声速机翼设计方法研究［J］.空气动力学学报，1999，17(3):327-331.

［10］DOWELL E H.A modern course in aeroelasticity［M］.SIJTHOFF ＆ NOORDHOFF International Publisher，1978.