脊状表面流场数值计算方法研究

胡海豹，宋保维，刘占一，黄桥高，潘 光

(西北工业大学航海学院，陕西 西安 710072)

0 引言

从仿生学角度探索降低航行体阻力的高效途径，一直是减阻研究领域内学者最为热衷的研究课题之一。中国科学院童秉纲院士也曾在香山科学会议的报告中称，鱼类等水生动物和有翼昆虫等飞行动物经历了亿年的进化过程，为了攫取食饵、逃避敌害、生殖繁衍和集群活动等生存需要，在漫长的适应环境的自然选择过程中，发展了各具特色的在水中游动和空中飞行的非凡能力，其整体功能渐趋优化，为当前的人造航行器和飞行器望尘莫及［1］。

人类在对海洋鱼类的研究中惊讶地发现，鲨鱼速度一般在50km/h左右，箭鱼速度甚至可超过130km/h。海洋动物以其柔弱的身躯，却能达到配备强大动力的舰船所难以企及的速度，在广阔的大海里遨游穿梭……。学者对鱼类外形的深入观测发现，鲨鱼、箭鱼等鱼类之所以具有良好阻力特性，一方面在于其拥有良好的流体动力外形，还有一个重要的原因就在于鱼类表皮上遍布着脊状结构(图1为不同种类鲨鱼局部表皮的电子显微镜扫描图［2］)。正是这些独特的脊状结构的存在，有效降低了其在水中游动时所受的阻力。另外，在长期经受大风洗礼的广袤沙漠里，也遍布着与海洋鱼类表皮结构类似的沙丘结构(如图2所示)。

受此启发，国内外学者开始关注脊状表面减阻技术的研究。自20世纪80年代初，NASA兰利研究中心Walsh、Wilkinson、Choi等先后报道了大量不同截面形状纵向脊状表面的减阻试验结果，并得到了最大约8%的减阻量。目前国外在该技术领域已进入工程测试阶段，如空中客车将A320试验机表面积的约70%贴上脊状表面薄膜，达到了节油1% ～2%的效果;NASA兰利中心在Learjet型飞机上开展的类似飞行试验显示，脊状表面的减阻量约为6%左右［3］。国内从20世纪90年代初才开始关注沟槽表面减阻技术的研究，如西工大宋保维等完成的纵向脊状表面水洞及风洞实验获得了超过6%的实验室减阻量［4］;北航王晋军等相继报道的纵向脊状表面测力及流场测试实验表明，纵向脊状表面局部阻力减少高达 13% ～ 26%［5］;西交大宫武旗［1，6］等报道的纵向脊状表面风洞试验也得到了约7%的减阻量。与纵向脊状表面减阻研究相比，横向脊状表面减阻属减阻研究的新领域，在国内外均无较全面的报道。

图1 不同种类鲨鱼局部表皮的放大照片Fig.1 Partial skin photograph of sharks

图2 沙漠里的沙丘Fig.2 Photograph of sandbank in a desert

为促进对脊状表面微观流场的认识，论文则着重探讨脊状表面流场数值计算方法研究，为脊状表面减阻机理的研究提供参考。

1 脊状表面流场数学模型

1.1 控制方程的确定

目前湍流数值模拟方法有三种:直接数值模拟(DNS)，大涡数值模拟(LES)，雷诺平均数值模拟(RANS)［7］。三种湍流数值模拟方法应用于相同雷诺数条件下流场理论计算时，直接数值模拟的网格尺度最小，所以要求计算机的内存最大，计算时间最长。雷诺平均数值模拟方法的网格尺度允许较大，因此要求计算机的内存小，计算时间短;大涡数值模拟则介于两者之间［8］。

脊状表面减阻理论研究中，主要涉及脊状结构内部及附近流场内主要旋涡的发生和发展。三种湍流数值模拟算法中，直接数值模拟需要超高计算量、算法本身尚不成熟;大涡模拟与雷诺平均数值模拟同样需要在近壁面采用壁面律来近似，但雷诺平均数值模拟方法计算量相对较小，且能够提供脊状结构内部主要旋涡分布等微观流场信息［9］。经综合权衡，本文采用了雷诺平均的数值模拟方法。脊状表面流场的控制方程如下:

连续方程:

雷诺平均Navier-Stokes方程:

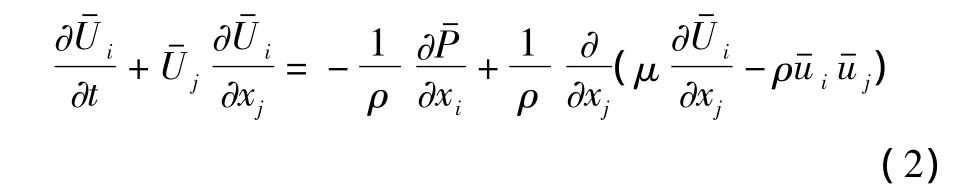
由于所模拟的时均流场属定常流动，将上述公式化简并在各个坐标轴上展开:

1.2 湍流模型的选择

目前常用的湍流模型很多，但每种湍流模型均有一定的使用范围要求。经过对标准k-ε模型、RNG k-ε模型等多种湍流模型的试用发现，相比其它湍流模型，RNG k-ε模型具有两特点:(a)通过修正湍流动粘度考虑了平均流动中的旋转及旋流流动的影响;(b)在ε方程中增加了反映主流时均应变率的项。因此，该模型可以更好地处理高应变率及流线弯曲程度较大的流动［10］，也更适合于脊状表面近壁区旋涡流动的仿真。该模型的方程形式如下:

其中，η0=4.377，β =0.012，Cμ=0.0845，αk= αε=1.39，C2ε=1.68。其它各项的具体计算公式如下:

2.3 边界条件的设置

为解决网格数量与硬件条件、计算精度与收敛速度之间的矛盾，论文根据所选控制方程的类型，联合使用了对称边界条件与周期性边界条件等［11］。典型的计算域边界定义如下:

(1)纵向脊状表面时，沿z轴方向左、右两边为一对周期性入口和出口;

(2)横向脊状表面时，沿z轴方向左、右两边为速度入口和自由流出口;

(3)沿y轴方向上，上表面设置为光滑平板表面，下表面设置为脊状表面;

(4)沿x轴方向两侧为对称面边界条件。

2 脊状结构表面网格剖分方法

2.1 脊状表面计算域的建立

2.1.1 纵向脊状表面计算域的建立

针对纵向脊状表面的形状特点，本文采用三维流场模拟计算方法，将计算域选定为脊状表面沿流向的一段三维空间。由于脊状结构的尺寸微小，这就要求在脊状结构表面的网格尺寸应足够的小;而另一方面由于计算资源的限制，整个计算域的网格总数又不能太大。反复的试算结果表明，纵向脊状表面流场粘性的影响在10倍脊峰高度处已经可以忽略。为尽量减少网格数量，本文取计算域高度等于10倍脊峰高度。因此，纵向脊状表面的计算域最终尺寸选取为Lx=20h，Ly=10h，Lz=10s(如图3所示)，其中h为脊峰高度，s为脊状结构宽度。

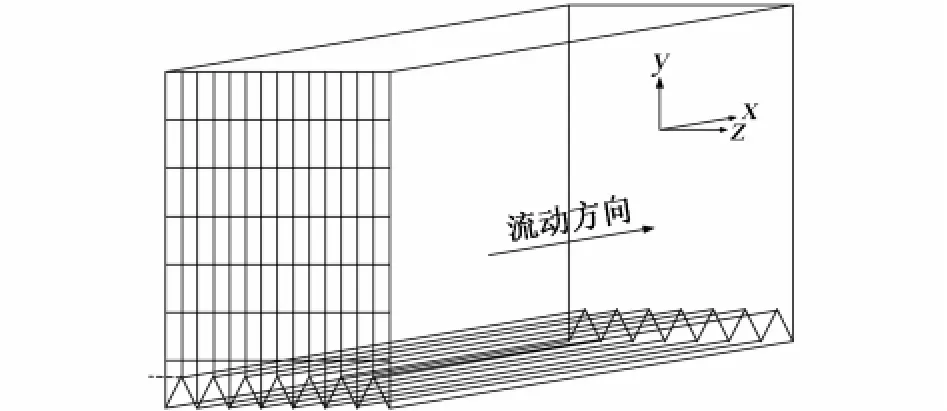
图3 三维计算域示意图Fig.3 Three-dimensional computation region sketch

2.1.2 横向脊状表面计算域的建立

横向脊状表面在展向方向的每个截面上具有完全相同的结构，可近似为二维流场。鉴于脊状表面主要在湍流状态下具有减阻效果，因此模拟计算时，必须保证脊状表面的流场处于充分发展的湍流状态。为此，论文在所模拟的脊状表面之前设置了一段流动发展段(对于平板表面流动，雷诺数超过5×105时才能达到湍流状态。为此，论文算例中，针对不同流速范围，在其计算域前端设置了不同长度的流动发展段)。同时为排除计算域出口对脊状表面流场的干扰，论文在所模拟脊状表面之后又设置了一段平板流动段。另外，本文将横向脊状表面计算域的高度也取为10倍脊峰高度。所以最终确定的计算域如图4所示。

图4 二维计算域示意图Fig.4 Two-dimensional computation region sketch

2.2 脊状表面网格剖分策略

CFD技术中，网格质量好坏将直接影响计算结果的精度。要真实模拟一个流动问题，必须结合具体问题建立满足计算精度要求的网格。作者在开展脊状表面流场数值模拟研究的过程中，针对脊状表面流场计算域的特点，总结了四条脊状表面网格剖分策略:

(1)脊状结构具有很好对称性和周期性，可采用缩小计算域的方法来提高脊状结构表面上网格的分辨率。本文中，脊状表面的计算域仅选取相邻的数个脊状结构。

(2)由于脊状表面计算域的几何形状比较复杂，且在脊状结构的脊峰处存在尖角，使得在脊状结构上难以剖分高质量的结构化网格。为此，可采用非结构化网格剖分技术［12］。

(3)针对脊状结构底部流动速度较小而顶部较大的特点，采用网格尺寸函数和计算域分区两种网格控制方法，可实现脊状表面网格分布呈底(脊谷)疏顶(脊峰)密的特点。

(4)为比较相同条件下脊状表面和平板表面流场特性的差异，同时又减小计算量，将与脊状表面(下表面)相对应的平板面(上表面)设置为壁面，即可将脊状表面和平板表面流场的数值模拟融合于同一算例中。

2.3 典型脊状结构的网格剖分

图5～图9为根据上述脊状表面网格剖分策略，生成的脊状结构表面网格图。其中，图5～图7为横向状态下V型、圆弧型、U型脊状表面二维计算域内网格局部放大图，图8～图9为纵向状态下V型、U型脊状表面三维计算域内网格局部放大图。

图5 V型脊状表面计算网格局部放大图Fig.5 Partial enlargement grid figure of V-riblets

图6 圆弧型脊状表面计算网格局部放大图Fig.6 Partial enlargement grid figure of Semicircular riblets

图7 U型脊状表面计算网格局部放大图Fig.7 Partial enlargement grid figure of U-riblets

图8 V型脊状表面计算网格Fig.8 Grid figure of V-riblets

图9 U型脊状表面计算网格Fig.9 Grid figure of U-riblets

3 脊状表面流场模拟实例

3.1 横向脊状表面流场模拟

图10所示为水速5m/s时不同形状脊状表面速度分布矢量图，图11为相同速度下不同形状脊状表面的静压强分布图，图12则为不同速度下不同间距横向U型脊状表面减阻曲线。综合分析图10～图12所示的横向脊状表面流场仿真结果可以发现:

图12 不同间距横向脊状表面减阻曲线Fig.12 Drag reduction profiles above spanwise riblet surfaces with different space

1)从图10可以发现，脊状结构的存在致使在其脊谷中形成稳定的大小、形状和位置基本相同的低速旋涡。这些旋涡上部流动的方向与来流方向一致，而下部的流动方向与来流方向相反，且既没有向外扩散，也无明显的相互影响［10］。因此，在横向脊状结构的内部其壁面剪应力的方向与外部来流方向相反，即这些低速旋涡产生了粘性推力。

2)从图11可见，在每个横向脊状结构的迎流面处存在一片压强增大区域(该区域内静压力显著比背流面大)，而在脊状结构间的台阶平面段静压力与外流场基本一致。由此可见，横向脊状结构在产生粘性推力的同时，又伴随产生了一部分粘性压差阻力。

3)从图12(a)、图12(c)中可以看出，与光滑平板表面粘性阻力仅为粘性摩擦阻力不同，横向脊状表面粘性阻力包括粘性压差阻力和粘性摩擦阻力两部分，其中粘性压差阻力随脊状结构间距的增大迅速降低，而粘性摩擦阻力则随脊状结构间距的增大而增大(当脊状结构间距a=0时，粘性摩擦阻力为负值，即摩擦阻力为推动力)。因此，随脊状结构间距的增大，横向脊状表面的粘性阻力中压差阻力比重降低，摩擦阻力比重则不断提高。

4)从图12(b)、图12(d)中可见，横向脊状表面具有良好的减阻效果，最大减阻量超过10%，且在不同流速下横向脊状表面的相对减阻量均随脊状结构间距的增大呈现先增大后又减小的趋势。以s=h=0.1mm的V型横向脊状表面为例(其中s为脊状结构宽度，h为脊状结构高度)，当脊状结构间距等于脊状结构宽度(a=s)时，减阻效果相对较好。

3.2 纵向脊状表面流场模拟

图13所示为4m/s水速下流向中间横截面处V型脊状表面流向速度分布图，图14为相同工况下V型脊状表面旋涡分布图，图15为相同工况下V型脊状表面剪应力分布图，图16则为V型脊状表面减阻量随脊状结构无量纲宽度的变化曲线。综合分析图13～图16所示的纵向脊状表面流场仿真结果可以发现:

1)从图13(a)可以发现，在每一个脊状结构底部沿y向的速度变化较顶角处要缓慢的多，说明在其的底部存在着低速流带;从图14(b)可见，在纵向脊状表面近壁区流场仍能够分辨出粘性底层、过渡层及对数律层等分层结构［4］，但纵向脊状表面粘性底层增厚，对数律区上移，这与其它壁面湍流减阻技术研究中所得到的边界层流场结构变化规律相一致［3，11］。

图13 流向中截面上V型脊状表面流向速度分布图Fig.13 Velocity distribution of the middle cross-section above V-riblets

图14 流向中截面上V型脊状表面旋涡分布图Fig.14 Vortex distribution of the middle cross-section above V-riblets

图15 V型脊状表面剪应力分布图Fig.15 Wall shear stress distribution above V-riblets

图16 V型脊状表面减阻量随无量纲宽度的变化曲线Fig.16 Correlation between the none dimension riblet width and the drag reduction quantity of V-riblets

2)从图14可以看出，纵向脊状结构的存在使得在每个纵向脊状结构顶点(顶部)两侧存在一对稳定的反向“二次涡”。该“二次涡”对可能正是脊状表面近壁区湍流猝发过程中起主导作用的顺流向“反向旋转涡对”与纵向脊状结构相互作用的产物，其产生必然会削弱顺流向“反向旋转涡对”的强度，进而降低近壁区湍流猝发的强度［6，10］。

3)从图15可见，纵向脊状表面壁面剪应力沿流向基本保持恒定，且不同形状脊状表面壁面剪应力均从脊状结构的底部到顶部逐步增大，即脊状表面的高剪应力区主要出现在其顶部处，而在脊状结构内部剪应力明显较低。

4)从图16可见，纵向脊状表面的减阻量随脊状结构无量纲宽度s+(s+=s·u/μ，其中μ为运动粘性系数，u为当地摩擦速度)的变大而先增大后减小，且在s+=10～25的范围内均具有减阻效果，最大减阻量约6.5% ，这也与相关报道基本一致［3，11］。

4 结论

上述横向和纵向脊状表面流场模拟结果说明，论文所总结的数值计算方法不仅能够得到脊状表面的减阻特性，还可以获得脊状结构内部及附近流场内流速、旋涡等细微结构的分布规律，且仿真结果与已有相关文献报道基本相一致。因此，本文所总结的脊状表面流场数值计算方法具有很强的适应性，基于该方法的脊状表面流场数值计算研究将可为脊状表面微观流场结构及减阻机理探索提供理论参考。

［1］童秉纲，陆夕云.关于飞行和游动的生物力学研究［J］.力学进展，2004，34(1):1-8.

［2］BALL P.Engineering:shark skin and other solutions［J］.Nature，1999，400:507-508.

［3］王晋军.沟槽面湍流减阻研究综述［J］.北京航空航天大学学报，1998，24(1):31-34.

［4］王柯，宋保维，潘光.条纹沟槽表面水下航行器减阻实验研究［J］. 力学与实践，2005，27(2):18-21.

［5］王晋军，李亚臣.沟槽面三角翼减阻特性实验研究［J］.空气动力学学报，2001，19(3):283-287.

［6］宫武旗，李新宏，黄淑娟.沟槽壁面减阻机理实验研究［J］. 工程热物理学报，2002，23(5):579-582.

［7］张兆顺，崔桂香，许春晓.湍流理论与模拟［M］.北京:清华大学出版社，2005，9.

［8］KALITZIN G，MEDIC G，IACCARINO G，et al.Near-wall behavior of RANS turbulence models and implications for wall functions［J］.Journalof Computational Physics，2005，204(1):265-291.

［9］胡海豹，宋保维，潘光，等.鲨鱼沟槽表皮减阻机理的仿真研究［J］. 系统仿真学报，2007，19(21):4901-4903.

［10］KOK J C.Resolving the dependence on freestream values for the k/ε turbulence model［J］.AIAA J.2000，38:1292-1295.

［11］王福军.计算流体动力学分析［M］.北京:清华大学出版社，2004.

［12］刘超群.多重网格法及其在计算流体力学中的应用［M］.北京:清华大学出版社，1995.

［13］胡海豹，宋保维，毛昭勇，等.随行波表面减阻降噪机理探索［J］.火力与指挥控制，2007，36(10):1928-1932.

［14］王晋军，兰世隆，陈光.沟槽面湍流边界层结构实验研究［J］.力学学报，2000，32(5):621-626.