具p-Laplacian算子与积分边界条件的脉冲微分方程的正解

李培峦 ,袁合才

(1.河南科技大学数学与统计学院,河南洛阳 471003;2.华北水利水电学院数信学院,河南郑州 450045)

0 前言

微分方程加上脉冲条件便成为脉冲微分方程,脉冲微分方程描述方程在特定时刻经历瞬间状态改变,反映微分方程在某个时刻的突变,能够比较精确和逼真地描述客观世界。最近十几年,脉冲微分方程理论在物理学现象、医学技术、人口动态、生物科技和经济数学模型中变得越来越重要[1-2]。

带有积分边界条件的微分方程(边值问题)理论出现在应用数学和物理的不同领域。例如,热传导、化学工程、地下的水流量、热弹性、等离子物理学等很多问题都可以转化为带有积分边界条件的微分方程边值问题。有关带有积分边界条件边值问题的重要性和相关理论,可参阅文献[3-4]。近年来带积分边界条件的边值问题正解的存在性和多解性引起了广泛的关注,但直到目前对于脉冲微分方程的积分边界条件的边值问题,特别是带p-Laplacian算子的脉冲微分方程积分边界条件的边值问题讨论的文章很少。至今为止只在文献[5-8]中看到对脉冲微分方程的积分边界条件的边值问题的研究,而对于带p-Lap lacian算子的脉冲微分方程的积分边界条件的边值问题结果更少。在文献[7]中,作者利用不动点指数理论讨论了下面的一类二阶的带p-Laplacian算子与积分边值条件的脉冲微分方程的边值问题:

本文讨论如下具p-Laplacian算子与积分边界条件的脉冲微分方程边值问题:

本文利用Leray-Schauder不动点定理得到了边值问题(1)的至少一个正解的存在性,本文所用的工具与文献[7]是截然不同的,非线性项的形式也更广泛,边值条件和所得结果也不同。

为了讨论边值问题(1),首先做如下假设:

(A 1) f∈C([0,1]×[0,+∞),[0,+∞))。

(A 2) g∈L1[0,1]非负,且σ∈(0,1),其中σ=∫g(t)dt。

(A 3) w(t)∈C([0,1],[0,+∞)),且在[0,1]的任何闭的子区间上w(t)≢0。

(A 4) Ik∈C([0,+∞),[0,+∞)),u()=u(tk+h),u()=u(tk-h)为u(t)在t=tk的右极限和左极限,k=1,…,n。

令E={u:[0,1]→[0,+∞)在t≠tk处连续,在点tk左连续,u(),u()存在且u()=u(tk), k=1,…,n};P={u∈E:u是[0,1]上的非负非降的凹函数,且u′(1)=0}。

x∈E∩C2([0,1]/{t1,…,tn},[0,+∞))称为边值问题(1)的正解,如果它满足边值问题(1),且x(t)≥0,∀t∈[0,1]。

1 主要引理

引理1[9](Leray-Schauder)E是一个Banach空间,A:E→E是一个全连续算子。如果集合{x:x∈E,x=λAx,0＜λ＜1}是有界的,那么算子A至少在 E中的闭球T上有一个不动点,其中,

在定义P后再做如下假设:

(A 5) 存在常数ck,使得≤ck,k=1,…,n,∀u∈P。

引理2 假设(A2)和假设(A4)满足h(t)∈C[0,1],且h(t)≥0,则u(t)是如下边值问题:

的解当且仅当u(t)是如下积分方程:

的解,且u(t)≥0。

证明 对式(2)中的第1个方程从t到1积分得:

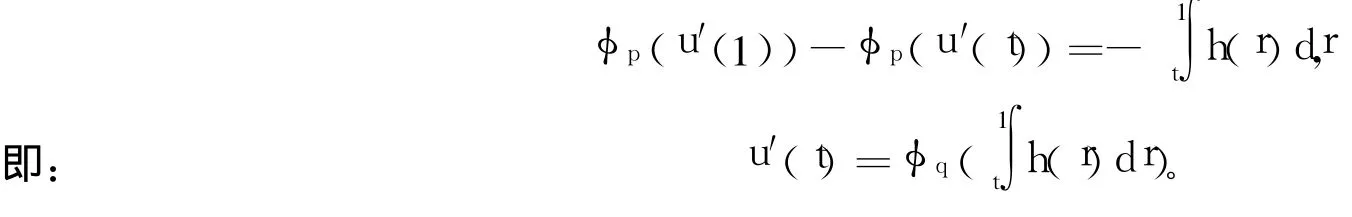
再对上面的微分方程从0到 t积分有:

因而:

由式(4)和式(5)可得:

反过来,若u(t)是积分方程(3)的解,求导可得:

由式(3)还可得:

再对式(6)求导可得:

因此,u(t)满足边值问题(2)的所有条件,故是问题(2)的解。

如果h(t)≥0,由式(3),假设(A2)和假设(A4)易得u(t)≥0。因而完成引理的证明。

定义算子A:

∀y∈P,由假设(A1)和假设(A3),引理2及算子A的定义可知:

则Ay∈P。故A是一个从P到P的算子。

据引理2可知欲得边值问题(1)正解,仅需讨论算子A的不动点。

其次,证明A:P→P一致有界。对d＞0,定义闭球Bd={u∈P∶≤d}。由(A5)和A的定义,∀u∈Bd,有:

最后证明{Au∶u∈Bd}等度连续。令t,t′∈[0,1],t＜t′;Bd={u∈P∶≤d}是P的闭凸子集,则当t→t′时,由假设(A1)、(A3)、(A4)易知(Au)(t′)-(Au)(t)→0。故算子族{Au:u∈Bd}等度连续。则由Ascoli-Arzela定理知,A:P→P全连续。

2 主要结果

本文的主要结果是应用引理1(Leray-Schauder不动点定理)得到的。

证明 令N(A)={u∈P:u=λAu,∀0＜λ＜1}。下证集合N(A)有界。

据假设(A1)、(A3)、(A5)可知N(A)有界。应用引理1可知:算子A至少有一个不动点u(∈P),即边值问题(1)至少有一个正解u(∈P)。

3 结论

[1] Bainov D D,Simeonov P S.Im pulsive Differential Equations:Periodic Solutions and Applications[M].Harlow:Longman Science and Technical,1993.

[2] Lakshmikantham V,Bainov D D,Simeonov P S.Theory of Impu lsive Differential Equations[M].Singapore:World Scientific,1989.

[3] Corduneanu C.Integral Equations and Applications[M].Cambridge:Cambridge University Press,1991.

[4] Agarwal R P,Regan D O.Infinite Interval Problems for Differential,Difference and Integral Equations[M].Dordrecht: Kluwer Academ ic Publishers,2001.

[5] Tian Y,Ji D,Ge W G.Existence and Nonexistence Resu lts of Impulsive First-order Prob lem with Integral Boundary Condition[J].Nonlinear Anal,2009,71:1250-1262.

[6] Zhang X M,Feng M Q,GeW G.Existence of Solutions of Boundary Value Problems with Integral Boundary Conditions for Second-order Im pu lsive Integro-differential Equations in Banach Spaces[J].JComput ApplMath,2010,233:1915-1926.

[7] Feng M Q,Du B,Ge W G.Impulsive Boundary Value Problem s with Integral Boundary Conditions and One-dimensional-Lap lacian[J].Nonlinear Anal,2009,70:3119-3126.

[8] Zhang X M,Yang X,Ge W G.Positive Solutions of nth-order Impu lsive Boundary Value Problems with Integral Boundary Conditions in Banach Spaces[J].Nonlinear Anal,2009,71(12):5930-5945.

[9] 郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,1983.