风力发电为主导的孤立发电系统可靠性评估

鲍莎日娜，栗文义，巴根，高飞

(1．内蒙古工业大学电力学院，呼和浩特市，010080;2．马尼托巴水电系统规划部，加拿大温尼伯，R3T0P4;3．北方联合电力有限责任公司，呼和浩特市，010010)

0 引言

未通电地区大多远离城镇和电网覆盖区，用电负荷小且分散，依靠电网延伸来供电，则经济性不佳。目前，这些地区主要依靠柴油发电供电。由于燃料价格不断上涨，柴油发电成本不断提高;另一方面，这些地区风力资源丰富，风能利用潜力很大;因此，为了向这些地区提供电力、节省柴油燃料和保护当地的生态环境，采用风力发电供电很有意义。由于风能有很强的随机性，风力发电系统一般需要配备储能设备(如蓄电池组)或采用风/柴联合运行的方式来提高发电系统的可靠性［1］。考虑到内蒙古的特定情况，需要一种有效的评估方法来评估风/柴/储能联合发电系统的可靠性［2］。

目前，电力系统可靠性评估的方法主要分为解析法和Monte Carlo模拟法两大类［3］。解析法的主要缺点是不能体现风速的时序变化特性，以及这种特性对风/柴/储能发电系统可靠性的影响。Monte Carlo模拟法中非序贯法的主要缺点是难以准确地计算与故障持续时间及故障频率有关的可靠性指标。而序贯Monte Carlo模拟法可以解决这些问题［4］，计算失负荷期望值(loss of load expectation，LOLE)、预期缺电量期望值(loss of energy expectation，LOEE)和失负荷频率(loss of load frequency，LOLF)等可靠性指标。

1 模拟方法

1．1 风速及风能转换系统模型

风力发电机(wind turbine generator，WTG)的小时输出功率取决于某地区的小时风速，风速随时间及风机安装地点的变化而变化，某一时刻的风速与先前的风速历史数据呈现一定的相关性。因此，为了体现风速时序性及相关性的特点，采用文献［5-6］描述的时间序列模型，应用某一特定地区已测量得到的风速历史数据，建立能够体现时变特性的风速模型。

时间序列模型中，用t时刻的风速均值μt及方差 σt计算预测风速 SWt［7］:

用历史风速时间序列yt-i建立风速时间序列模型ARMA(n，m)，又称作自回归滑动平均模型:

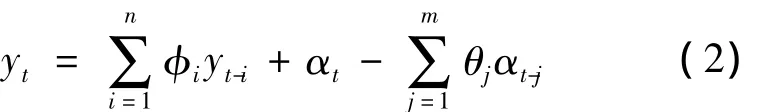
式中:φi(i=1，2，3，．．．，n)和 θj(j=1，2，3，．．．，m)分别为模型的自回归参数和滑动平均参数;{ αt}为正态白噪声序列，元素 αt服从均值为0、方差为的正态独立分布，即

用模拟得到的小时风速序列，计算WTG的小时输出功率序列［7-8］:

其中:

式中:Pr为风电机额定输出功率;vci、vr和vco分别为风力机的启动风速、额定风速和切出风速。

1．2 蓄电池模型

由于WTG的输出具有间歇性，所以需要配备储能设备(如蓄电池组)来提高风/柴/储能发电系统的可靠性。蓄电池组的充放电状态时间序列由发电系统时间序列和负荷时间序列获得［9］。

(1)由发电时间序列 { WGt，t=1，2，3，．．．，T}和负荷时间序列 {Lt，t=1，2，3，．．．，T}得到冗余容量时间序列(其值可正可负){SGt，t=1，2，3，．．．，T}:

(2)计算蓄电池组充放电状态时间序列 {Bt，t=1，2，3，．．．，T}:

式中:BM和Bm分别为蓄电池组最大、最小允许存储容量。

1．3 风/柴/储能发电系统可靠性评估模型

风/柴/储能发电系统可靠性评估模型如图1所示［10］。负荷模型采用IEEE-RBTS可靠性测试系统模型［11］，它是按时间顺序排列的8 736 h的负荷标幺值，系统峰值负荷为40 kW。

图1 风/柴/储能发电系统可靠性评估模型Fig.1 Reliability evaluation model of power system co-generated by wind，diesel and energy storage

2 样例系统分析

本文采用内蒙古某风电场的风速历史数据，应用前述方法对风/柴/储能联合发电系统进行可靠性评估，系统配置及参数如表1。WTG的切入风速、额定风速、切出风速分别为12，38，80 km/h;评估过程中不考虑蓄电池的强迫停运;风电场平均风速和标准差分别为22.302，10.872 km/h;根据风速历史数据，应用Matlab中的Armax函数计算得到时间序列模型的阶数、自回归参数和滑动平均参数;那么，代表此风电场的风速时间序列模型ARMA(4，3)为

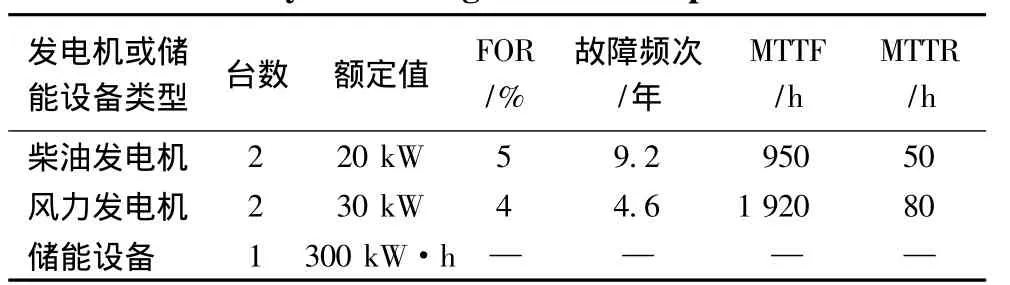
表1 系统配置及参数Tab.1 System configurations and parameters

2．1 仿真样本容量对可靠性的影响

序贯Monte Carlo模拟法中的样本容量不是所抽取的系统状态数，而是抽样过程跨越的年数［12］。为了分析仿真样本容量大小对系统可靠性指标收敛程度的影响，把可靠性指标看作仿真样本容量的函数。系统数据如表1所示，样本容量从100变化到1 000，步长为100。仿真结果如图2～4。图2～4表明:如果仿真样本容量较小，可能会导致可靠性指标的收敛速度较慢，距离期望值的偏差较大;随着仿真样本容量变大，系统可靠性有所提高，且仿真样本容量越大，系统可靠性指标越趋于一个定值，这个定值被称作可靠性指标的期望值;由此曲线可确定系统可靠性指标的期望值。

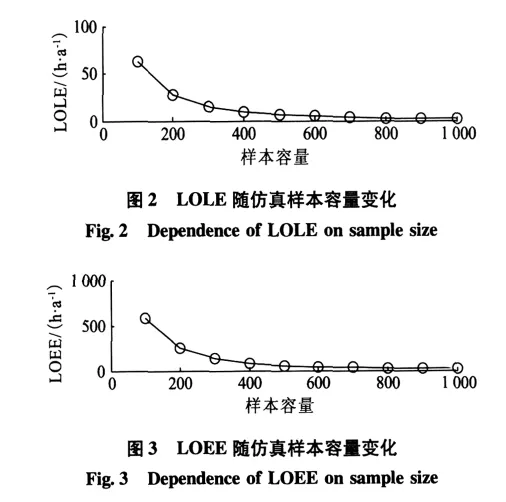
图4 LOLF随仿真样本容量变化Fig.4 Dependence of LOLF on sample size

2．2 风力发电总容量不变时，WTG容量对可靠性的影响

表2列出了4种不同发电系统的可靠性指标。系统数据如表1所示，改变WTG的台数及额定值，但WTG的其他参数和系统其他配置不发生变化，对4种情况进行模拟计算。表2表明:(1)风力发电容量一定时，系统可靠性随WTG单机容量的减小而提高，这是因为，系统风力发电容量一定时，机组容量越小，机组数量越多，机组故障对系统可靠性影响就越小;(2)虽然系统总的发电容量远超过系统的峰值负荷，但在没有安装蓄电池的情况下，LOLE、LOEE和LOLF都高到了可靠性评估不可接受的水平，装设蓄电池后，系统可靠性明显改善。

2．3 蓄电池最大充放电率对可靠性的影响

为了分析蓄电池最大充放电率对可靠性的影响，把可靠性指标看作蓄电池最大充放电率的函数。系统数据如表1所示，蓄电池最大充放电率从5(kW·h)/h变到50(kW·h)/h，步长为5(kW·h)/h，对2种具有不同蓄电池容量的系统进行模拟，仿真结果如图5～7所示。图5～7表明:随着蓄电池最大充放电率的增大，LOLE、LOEE和LOLF呈明显的递减趋势;最大充放电率增大到一定值［本文为40(kW·h)/h］后，继续增大该值，对系统可靠性影响不明显，可靠性指标几乎稳定在一个常数附近，60(kW·h)/h为该系统蓄电池最大充放电率的合适值。

2．4 风力发电机额定功率的影响

为了分析WTG额定功率对系统可靠性的影响，把可靠性指标看作WTG额定功率的函数。系统数据如表1所示，每台WTG的额定功率从20 kW变化到160 kW，步长为20 kW。仿真结果如图8～10。图8～10表明:随着WTG额定功率的增大，系统可靠性不断提高。由图8～10中的曲线可确定WTG的额定功率和相应的蓄电池容量。

表2 WTG单机容量变化时系统可靠性指标(风力发电系统总容量:60 kW)Tab.2 Reliability index of system with the changing of single-machine capacity of WTG where the total capacity is 60kW

图10 LOLF随WTG额定功率变化Fig.10 Dependence of LOLF on rated power of WTG

2．5 柴油发电机额定功率的影响

为了分析柴油发电机额定功率对系统可靠性的影响，把可靠性指标看作柴油发电机额定功率的函数。系统数据如表1所示，每台柴油发电机的额定功率从15 kW变化到50 kW，步长为5 kW。仿真结果如图11～13。图11～13表明:随着柴油发电机额定功率的增大，系统可靠性有明显提高。图11～13中的曲线可为柴油发电机的配置提供一定的依据。

3 结论

本文详细描述了风/柴/储能联合发电系统的可靠性评估模型。针对样例系统，考虑了一些影响系统可靠性的因素，计算和分析了联合发电系统的一些可靠性指标。结果表明:风/柴/储能联合发电系统的可靠性受仿真样本容量、蓄电池容量、蓄电池最大充放电率、WTG额定功率和柴油发电机额定功率等诸多因素影响。本文采用的模型及方法可为政府及电力部门推广风/柴/储能联合发电向偏远地区供电提供依据;可为内蒙古地区及一些孤立岛屿采用以风力发电为主导的小型孤立系统发电提供依据。

［1］Billinton R，Bagen，Cui Y．Reliability evaluation of small standalone wind energy conversion systems using a time series simulation model［J］． IEEE Proceedings-Generation，Transmission and Distribution，2003，150(1):96-100．

［2］刘威，赵渊，周家启．计及风电场的发输电和配电系统可靠性评估［D］．重庆:重庆大学电气工程学院，2008．

［3］Billinton R，Chen H．Assessment of risk-based capacity benefit factors associated with wind energy conversion systems［J］．IEEE Transactions on Power Systems，1998，13(3):1191-1196．

［4］Billinton R，Li W Y．Reliability assessment electric power systerms using monte carlo methods［M］.New York:Plenum Press，1994．

［5］丁明，张立军，吴义纯．基于时间序列分析的风电场风速预测模型［J］．电力自动化设备，2005，25(8):32-34．

［6］邵璠，孙育河，梁岚珍．基于ARMA模型的风电场风速短期预测［J］．电网与清洁能源，2008，24(1):52-55．

［7］Billiton R，Gan L． Wind powermodelingand application in Generating adequacy assessment［C］//IEEE Conference Proceedings on Communication，Computers and Power in the Modern Environment，Saskatoon，Canada，1993:100-106．

［8］包能胜，胡光旺，倪维斗．大型风电场整体风速功率模型研究［C］//工程热物理与能源利用学术会议，重庆，2006:364-372．

［9］Bagen，Billinton R．Impacts of energy storage on power sytem reliability performance［C］// 2005 IEEE CCECE/CCGEI，Saskatoon，Canada，2005:494-497．

［10］栗文义，张保会，巴根．风/柴/储能系统发电容量充裕度评估［J］．中国电机工程学报，2006，26(16):62-67．

［11］ Allan R N，Billinton R，Sjarrief I，et al．A reliability test system for educational purposes-basic distribution system data and results［C］//IEEE Transactions on Power Systems，Manchester，UK，1991:813-820．

［12］ Billinton R，Tang X．Selected considerations in utilizing Monte Carlo simulation in quantitative reliability evaluation of composite power systems［J］．Electric Power Systems Research，2004，69(2-3):205-211．