任意非空心旋转导体的自感系数

李肃成，李嘉亮

（常熟理工学院物理与电子工程学院，江苏常熟 215500）

任意非空心旋转导体的自感系数

李肃成，李嘉亮

（常熟理工学院物理与电子工程学院，江苏常熟 215500）

计算了单位长度圆柱导体、圆锥导体、半球导体以及椭圆柱导体的自感系数，发现其自感系数与形状无关，进而证明了任意非空心旋转导体的自感系数也与导体的粗细及形状无关.

非空心旋转导体；自感系数；安培环路定理

关于圆柱体同轴电缆自感系数的问题，理论上可以用两种方法进行讨论，但二者的结论不一致，对此我们通过分析给出了正确的解答.经过计算发现：圆柱体、圆锥体以及半球体的自感系数是相同的，在此基础上我们选取了任意非空心旋转导体这一几何模型，证明了其单位长度的自感系数与导体形状以及粗细无关.这个普遍结论尚未见有学者报道.

1 基本理论

电磁学中［1,2］，求解自感系数通常有三种方法：

本文主要采用（1）式和（2）式来探究导体的自感系数.而在利用（1）式求解自感系数的时候，会出现对磁通量的概念理解不够透彻而容易犯的一个很普遍的错误.针对这个问题，我们给出了合理的解决方案.

2 几种特殊形状导体自感系数的讨论

2.1 圆柱导体的自感系数

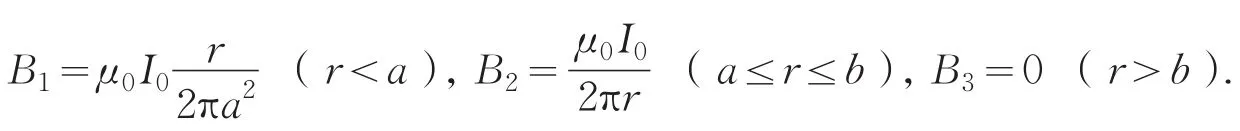
由（4）式可以看出，当外筒壁半径非常接近内圆柱半径时，上式第二项可忽略，从而得到单位长度实心圆柱导体的自感系数L与导体的半径a无关的结果.

m0同轴电缆的自感系数为显然（4）式和（5）式的结果并不一致，下面探讨产生此差异的原因［3］.

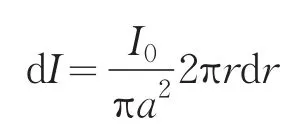
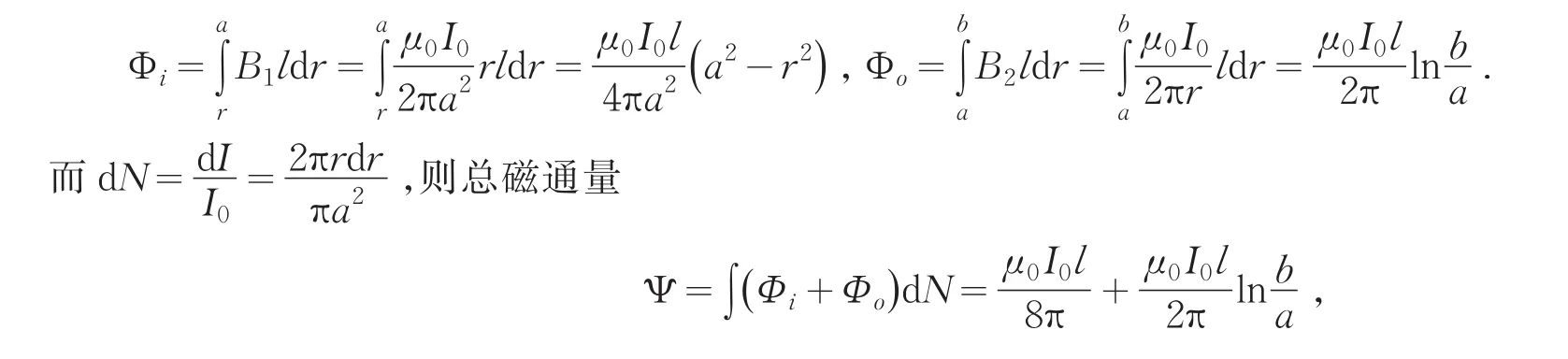
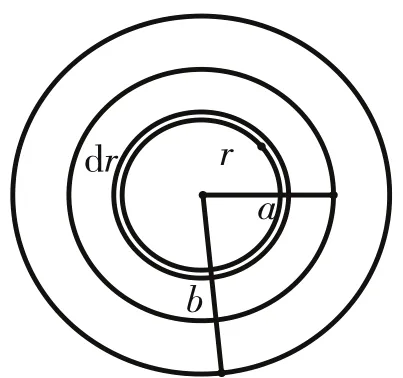
图1

若为单位长度的同轴电缆，则

这个结论与我们使用能量法所得的结论完全一致.其误差原因的分析其他学者也讨论过［4］.

2.2 圆锥导体的自感系数

由单位长度的实心圆锥体、半径为R的半无限长圆柱体以及半无限长细长导线所组成的无限长轴对称导体如图2所示，其内有均匀分布的稳恒电流流过［5］.文献[5]直接使用定义法及安培环路定理讨论了其自感系数，但对为什么可以应用安培环路定理未加剖析.因此，这里我们首先讨论安培环路定理的适用问题.

安培环路定理可表示为∮Β∙dl=μ0I环内，是Β的环流与环路中所包围的电流之间的关系.无论环路外是否存在电流、电流以何种角度穿过以环路为边界的平面，该方程都是成立的.但是该方程绝不是Β和I环内的关系，因为若环路外有电流的话，环路上任何一点的Β应是环路内、外电流共同产生的.因此，如果对称性破坏的话，即使已知方程的右边也无法求出某一点的Β.

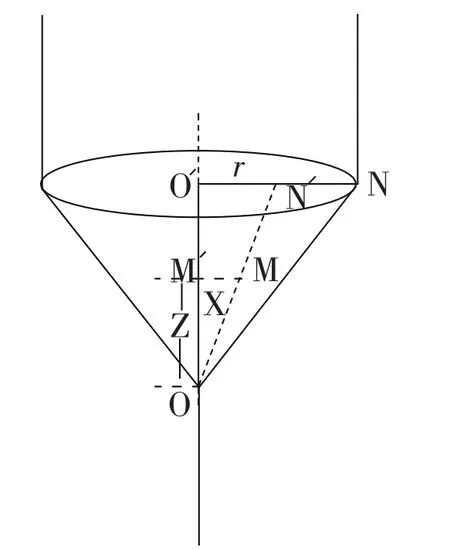
图2

在我们的模型中取锥体为研究对象.如图3所示，对M点而言，电流①和②在M点所产生的Β方向由纸面外向内，这恰好与环路dl的方向共线，即cosθ=1，所以∮Β∙dl=∮Bdl.此外，在以x为半径的圆周上，由于模型的均匀对称性，所以Β的大小相等，因此必有∮Β∙dl=μ0I环内⇒B∮dl=μ0I环内.注意：此式完全没有必要知道①、②电流是以什么角度穿过环路的.此外，还应该注意一个问题：电流①、②应该是从无限远来，到无限远去，否则安培环路定理也不适用.

还可以进一步考虑电流流向的磁效应问题.在图4中取M点及其对称点M″，而IM的大小与IM″的大小相等.从理论上我们可以将IM和IM″在x和z方向分解，注意到IMx和IM″x的大小相等，方向相反，所以对本问题而言，它们不产生磁效应，也就是说对垂直于轴的环面而言，由于旋转对称性，电流在该面内的磁效应为零.因此，在我们的模型中安培环路定理完全可以使用.

与文献[5]不同，我们将从能量的角度来讨论这个问题.由安培环路定理可以求得锥体内任意一点M的磁感强度，即

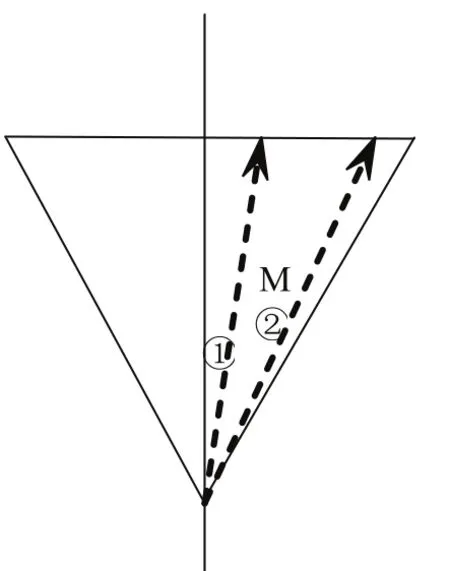
图3

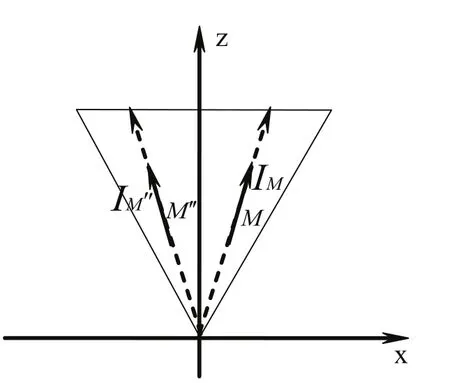
图4

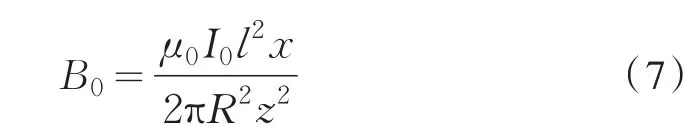
式中，x为M到轴线OO′的距离，z为垂足M′到圆锥顶点O的距离.于是，磁能

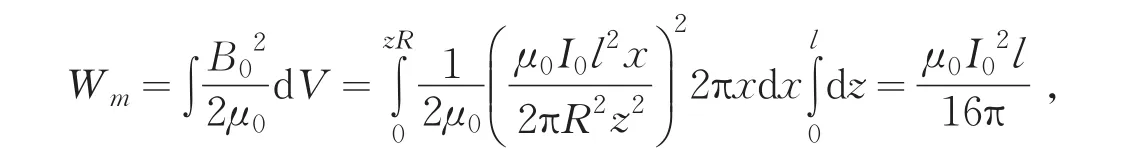
由（2）式得到单位长度导体的自感系数为

这一结果与文献[5]完全一致.

2.3 半球导体的自感系数

设由单位长度的实心半球体（即R=1）、半径为R的半无限长圆柱体以及细长导线所组成的无限长轴对称导体（见图5），其内有均匀分布的稳恒电流流过，求相应于半球导体的自感系数L.

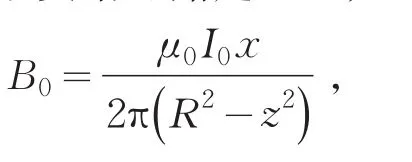
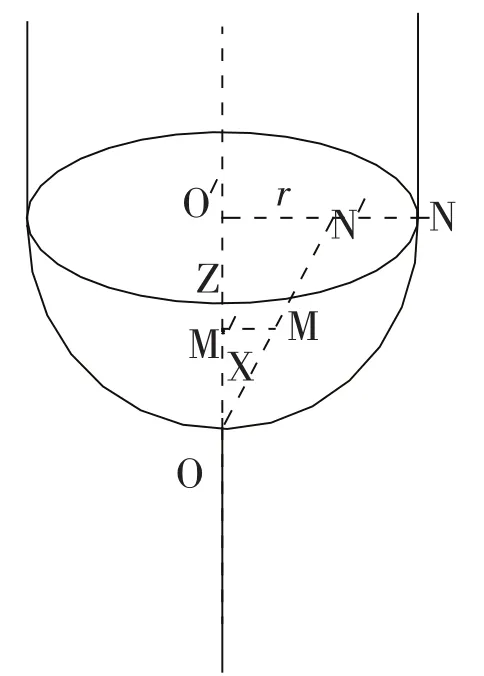
图5

则磁能

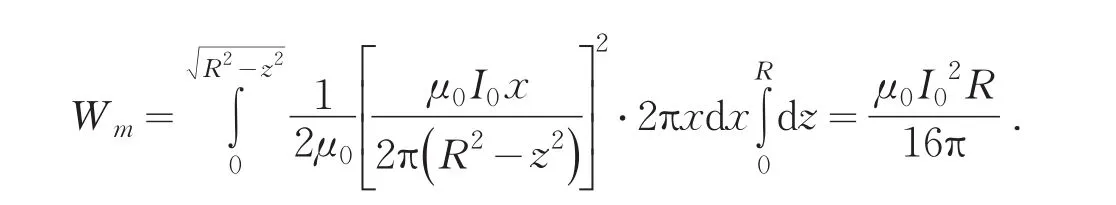
再由（2）式得到单位长度的实心半球体的自感系数为

3 非空心旋转导体的自感系数

上面四种几何模型得出的结论完全一致，由此我们可以设想任意非空心旋转导体（由一个平面图形绕这平面内一条直线旋转一周而成的且垂直于轴线的任意截面均是圆面的几何体）相应于内部的自感系数与导体的粗细以及形状无关.

由单位长度的任意非空心旋转实心导体以及两半无限长圆柱体所组成的无限长轴对称导体如图6所示，其内有均匀分布的稳恒电流流过，我们来求此非空心旋转导体的自感系数L.

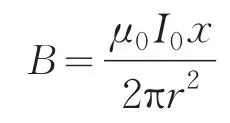
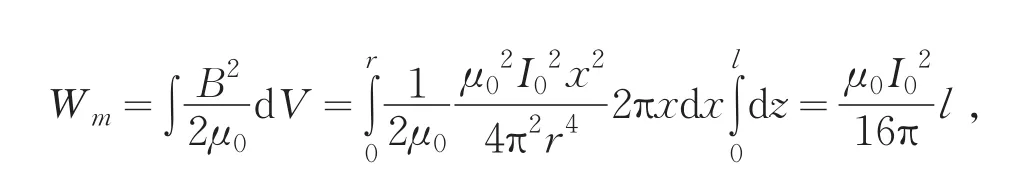
再由（2）式得到单位长度的电缆的自感系数为

即任意非空心旋转导体的自感系数与导体的粗细以及形状无关，这一结论至今尚未见有学者报道.

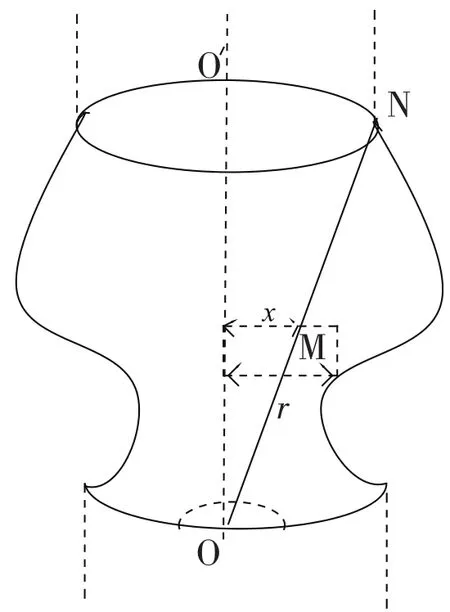
图6

4 椭圆柱体导体的自感系数

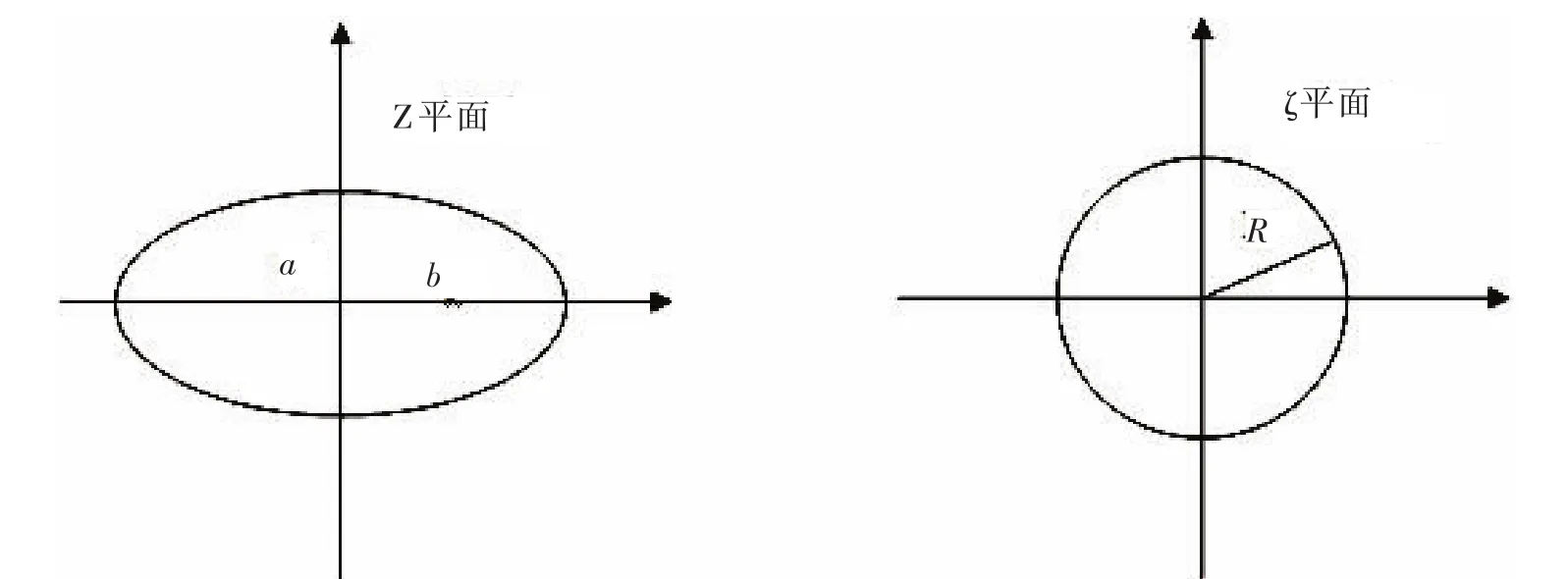
图7

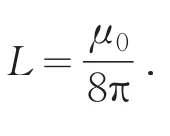
5 结语

在以上所构造的各种模型中，通过理论计算发现其自感系数是相同的.在可以忽略边界条件影响的情况下，所构造的这些模型是可以在实际电路中实现的（即实现以上模型中的无限长条件）.因而，以上结论也是可以通过实验验证的.我们期待实验学者能够对我们的结论给以检验.

[1]赵凯华.电磁学[M].第二版.北京：高等教育出版社，2003：192-194.

[2]程守洙.普通物理学（上册）[M].北京：高等教育出版社，2006：412-415.

[3]李梅.普通物理错例剖析[M].北京：机械工业出版社，1987：270-273.

[4]何贤美.求解电缆自感系数的一个佯谬[J].安徽工业大学学报，2002（1）：79-81.

[5]颜家壬.求三维导体自感系数的另一方法[J].大学物理，1984（10）：4-6.

[6]梁昆淼.数学物理方法[M].北京：高等教育出版社，1998：442-443.

[7]王福谦.椭圆柱电缆单位长度的自感计算[J].大学物理，2008（8）：19-20.

[8]熊宝库.儒可夫斯基变换及在物理学中的应用[J].河南教育学院学报（自然科学版），2003（1）：11-12.

Any Non-hollow Rotating Self-induced Coefficient of Conductor

LI Su-cheng,LI Jia-liang
(School of Physics and Electronic Engineering,Changshu Institute of Technology,Changshu 215500,China)

By calculating self-induced coefficient of cylindrical conductor,conical conductor,hemisphere con⁃ductor and elliptical conductor,this paper found it had nothing to do with the shape of conductor.Therefore,the paper proved any non-rotating hollow conductor inductance had no relationship with the thickness and shape of conductor.

non-hollow rotating conductor;self-induced coefficient;Ampere Theorem

O414.1

A

1008-2794（2011）08-0046-05

2011-05-12

李肃成（1987—），男，江苏盐城人，常熟理工学院物理与电子工程学院学生.

李嘉亮（1957—），江苏常熟人，常熟理工学院物理与电子工程学院教授，研究方向：凝聚态物理，E-mail:ljl@cslg. edu.cn.