单圈T函数输出序列k-错线性复杂度研究

罗小建 胡 斌

(解放军信息工程大学电子技术学院 郑州 450004)

1 引言

2002年，文献[1]提出了T函数的概念，并对其进行了系列研究。T函数是非线性的甚至是非代数的，并能在软件上快速实现，T函数先后用于分组密码，Hash函数和流密码的构造。

如果可逆T函数所决定的状态转移图的周期为2n，则称该T函数为单圈T函数。文献[1]提出用单圈T函数代替线性移位寄存器作为密钥发生器的驱动源的思想，因此，单圈T函数输出序列的稳定性成为研究的重点。安全强度高的序列不但具有高的线性复杂度，而且必须具有很好的稳定性，而序列的稳定性一般采用k-错线性复杂度表征。

国内外对单圈T函数输出序列线性复杂度的研究较少，2006年，文献[2]给出了单圈T函数输出序列的线性复杂度和k-错线性复杂度；2008年，文献[3]得到了单圈T函数按位输出的序列的线性复杂度以及k-错线性复杂度。本文对单圈T函数输出序列的k-错线性复杂度进行了深入研究，利用多项式理论和Chan Games算法，在输入规模2tn=时，分析得到了单圈T函数输出序列的线性复杂度的所有下降点，及其相应位置的k-错线性复杂度取值，并进一步给出该序列k-错线性复杂度的分布情况及k-错线性复杂度曲线。

2 准备知识

线性复杂度：设S=s0s1s2…是Z2上周期为N的序列，定义其形式化多项式s(x)为

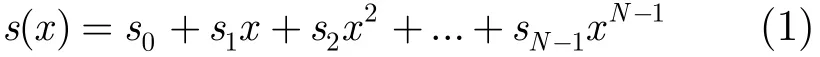
序列S的线性复杂度指产生此序列的线性反馈移位寄存器的最小阶数，记为LC(S)。文献[4]给出了周期序列S的线性复杂度的一个代数化描述，即

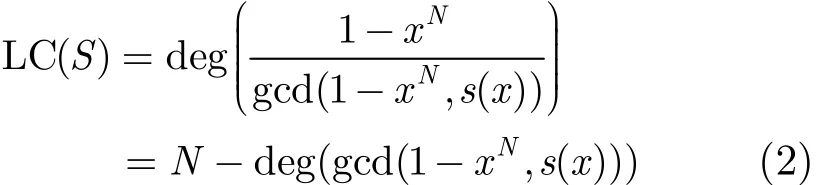
2.1 基本定义

定义1[1]设f(x)是Z/(2n)→Z/(2n)上的多输出函数，记f(x)=([f(x)]n−1,…,[f(x)]1,[f(x)]0)，如果其输出的第i位[f(x)]i仅与输入的第0至第i位，即([x]i,…,[x]0)有关，则称f(x)为T函数。其中[x]i,[f(x)]i表示x和f(x)的第i路分量，i=0,1,…,n −1。

显然，根据T函数的定义，可将T函数表示为如下形式：

其中fi(x)=fi([x]i,[x]i−1,…,[x ]0)为布尔函数。

定义2[1]若可逆T函数的状态转移图是单圈的，则称该函数为单圈T函数。

定义3[5]对一个周期序列S，每个周期改变小于或等于k比特后得到的新序列的最小线性复杂度，称为k-错线性复杂度，记为LCk(S)。

从定义可以看出，计算LCk(S)的一般方法为构造一个周期与S相同的序列e，一般称为错误序列，则LCk(S)=min{LC(S⊕e)|W(e)≤k }。

定义4[5]对周期序列S，定义minerror(S)为使得LCk(S)＜LC(S)的k的最小值。

定义5[5]设S是Z2上周期为N的序列，S的k-错复杂度曲线定义为S的k-错复杂度序列，即LC0(S)=LC(S),LC1(S),…,LCW(S)(S)。

2.2 单圈T函数输出序列

单圈T函数周期达到最大，即为2n，设si=(ai,0,ai,1,…,ai,n−1)为单圈T函数输出的第i个状态，1≤i≤n −1，称S(T)=(s0|s1|…|s2n−1……)为单圈T函数输出序列，其中si|si+1表示状态si和si+1的级联，即si|si+1=(ai,0,…,ai,n−1,ai+1,0,…,ai+1,n−1)。

引理1[1]设f(x)是单圈T函数，s0, s1,…,s2n−1表示f(x)在一个周期内的所有输出状态，设ai=(a0,i,a1,i,…,a2n−1,i,…)表示f(x)的第i分位序列，则(1)ai的周期为2i+1; (2)aj,i⊕aj+2i,i=1对j≥0都成立。

3 单圈T函数输出序列k-错线性复杂度研究

下面研究当n=2t时，单圈T函数输出序列的k-错线性复杂度的分布情况及k-错线性复杂度曲线。首先给出几个引理。

引理2[6]设S是周期为N的二元序列，若N=2t，则minerror(S)=2W(N−LC(S))。

引理3[7]令sm=(s0, s1,…,s2m−1)∈Z /(22m)，则S=(sm,sm,sm,…)是周期为2m的序列。记sm=(L(sm),R(sm))，其中L(sm)=(s0,…,s2m−1−1), R(sm)=(s2m−1,…,s2m−1)分别表示sm的左半部分和右半部分。令d=L(sm)⊕R(sm)，则当d为全零向量时，LC(S)=LC(L(sm))，当d不为全零向量时，LC(S)=2m−1+LC(d)。

由引理3可知，序列的周期越小，线性复杂度越小。

引理4[8]设k, t∈Z,k＜2t，则(1+x)k−1的项数为2W(k−1)。

引理5 设S是单圈T函数输出序列，记单圈T函数的第i分位序列为ai,ai改变若干比特后的序列记为bi，其周期为p(bi)，则对任意整数j,0≤j≤i，可在S的每个周期内通过改变a的2n−1i个比特得到bi，使得p(bi)=2j成立，其中0≤i≤n −1。

证明 设单圈T函数输出序列为S=(a0,0,a0,1,…,a0,n−1,a1,0,a1,1,…,a1,n−1,…,a2n−1,0,a2n−1,1,…,a2n−1,n −1,…)，显然S的周期p(S)=n×2n。设单圈T函数输出序列的第i分位序列ai=(a0,i,a1,i,…,a2i+1,i,…)，显然S的一个周期内第i分位序列的长度为2n，记为，由引理1知，

设bi=(b0,i,b1,i,…,b2j−1,i,…)是周期为2j的任一序列，0≤j≤i，并记表示bi的前t个比特，下面证明将变成需要改变2n−1个比特。

由于p(b)=2j|2i，显然，=(,)。i 变成需要改变x个不妨设将比特，0≤x ≤2i，即(a,a,…,)和有x个0,i1,i比特不同，2i−x个比特相同。再由引理1知，⊕=1，因此和有x个比特相同，2i−x个比特不同，进而要将(a2i,i,a2i+1,i,…,a2i+1−1,i)变成需要改变2i−x个比特。因此，要将(a,a,…,a)变成一共需要改变x+(2i−x)=2i个比特。又因为=2i+1|2n,由2n−1−i个(a,a,…,a)组成，故0,i1,i2i+1,i将变成需要改变2n−1−i×2i=2n−1个比特。

证毕

由引理5及其证明过程可知，对任意满足j＜i+1的非负整数j，在单圈T函数输出序列的一个周期内，改变分位序列ai的2n−1个比特，可使得改变后的序列bi为周期整除2i的任意序列。

定理1 设S是单圈T函数输出序列，当n=2t时，对任意的整数u,1≤u≤n −1，令k=u×2n−1,S的k-错线性复杂度为LCk(S)=n−u+n×2n−u−1。

设ai=(a0,i,a1,i,…,a2n−1,i,…)为输出序列的第i分位序列，0≤i≤n −1。由引理3可知，要将序列S的线性复杂度降低，在S的一个周期内改变相同比特数的前提下，改变后序列的周期越小，其线性复杂度越小。进一步地，根据序列S的特性和引理5可知，当S在每个周期内改变u×2n−1个比特时，其周期最小可以达到n×2n−u，即将an−u,…,an−1这u个分位序列分别改变2n−1个比特，使得改变后的分位序列周期整除2n−u。

设(1+x)u=1+c1x+…+cuxu，其中c1,…,cu∈Z2。对任意整数i(1≤i≤u)，若ci=0，将分位序列an−1−(u−i)在每周期内改变2n−1个比特使其变成全零序列；若ci=1，将an−1−(u−i)在每周期内改变2n−1个比特使其变成an−u−1。

因此，根据ci的取值，存在序列bn−1−(u−i)，满足周期为2n且W(bn−1−(u−i))=2n−1，使得an−1−(u−i)⊕bn−1−(u−i)=cian−u−1,i=1,2,…,u 。令错误序列为=(0…0b0,n−u… b0,n−1,0…0b1,n−u…b1,n−1, …,0…0其中(0…0bi,n−u…bi,n−1)中含有n个比特，i=0,1,…,2n−1，则W()=u×2(n−1),S⊕的周期为n×2n−u。设S⊕的形式化多项式为s'(x)，即

其中

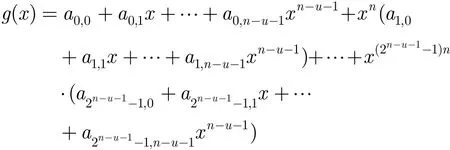
则

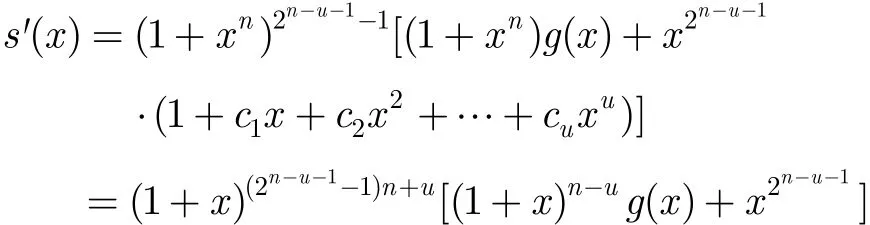
设S是二元周期序列，记err1(S)为使得LCk(S)＜LC(S)成立最小的k，称err1(S)为序列S线性复杂度的第1下降点，显然err1(S)=minerror(S)；记err2(S)为使得LCt(S)＜LCk1(S)成立最小的t，其中k1=err1(S)，称err2(S)为序列S线性复杂度的第2下降点。同样可得到第3,…，第k下降点的定义。显然1≤err1(S)＜…＜errk(S)＜…且LC(S)＞LCerr1(S)(S)＞…＞LCerrk(S)(S)＞…。

下面给出当n=2t时，单圈T函数输出序列线性复杂度的第u下降点erru(S)及当k=erru时，LCk(S)取值。

定理2 设S是单圈T函数输出序列，当n=2t时，对任意整数u,1≤u≤n −1,S的线性复杂度的第u下降点erru(S)=u×2n−1，且LCk(S)=n−u+n×2n−u−1，其中k=err(S)。

证明 当u=1时，err1(S)=minerror(S)=2W(n×2n−1−n×2n−1−n)=2n−1，由引理5可知，LCk(S)=n−1+n×2n−2，其中k=err1(S)，故此时结论成立；

假设当u=h时，err(S)=2h×(n−1)且LCk(S)=n−h+n×2n−h−1，其中k=errh(S)，由定义可知，存在错误序列满足周期为n×2n且W()=h×2n−1，使得LC(S⊕)=n−h+n×2n−h−1。

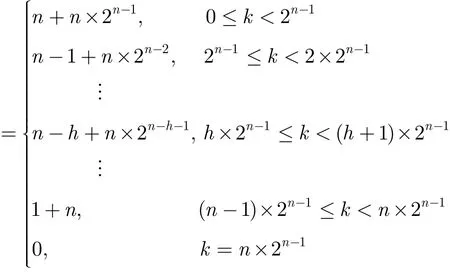
定理3的证明可直接由LCk(S)的定义、定理2及其推论得到，在此不再进行证明。

基于上述讨论，可以得到当n=2t时，单圈T函数输出序列的k-错线性复杂曲线，如图1所示：

图1 单圈T函数输出序列k-错线性复杂度曲线

图1形象地描述了当n=2t时，单圈T函数输出序列的k-错线性复杂的变化情况，图中横坐标k表示序列S在一个周期内改变了k个比特，纵坐标LCk(S)表示序列S的k-错线性复杂度取值。

4 结束语

本文分析了当n=2t时，单圈T函数输出序列的k-错线性复杂度分布情况及k-错线性复杂度曲线。对于单圈T函数输出序列来说，在输入规模为任意取值时，单圈T函数输出序列的k-错线性复杂度的分布和k-错线性复杂度曲线都是非常有意义的问题，值得进一步研究。

[1] Klimov A and Shamir A. A new class of invertible mappings.Workshop of CHES 2002, Springer Verlag, 2003, LNCS 2523:470-483.

[2] Zhang W Y and Wu C K. The algebraic normal form, linear complexity and k-error linear complexity of single-cycle T-function. Proceedings of SETA 2006, LNCS 4086, Springer Heidelberg, 2006: 391-401.

[3] 赵璐, 温巧燕. 单圈T函数输出序列的线性复杂度及稳定性.北京邮电大学学报, 2008, 31(4): 62-65.Zhao Lu and Wen Qiao-yan. Linear complexity and stability of output sequences of single cycle T-function. Journal of Beijing University of Posts and Telecommunications, 2008,31(4): 62-65.

[4] Cusick T, Ding C, and Renvall A. Stream ciphers and number theory. North-Holland, Elsevier, 1998.

[5] Ding C, Xiao G, and Shan W. The stability theoery of stream ciphers. Springer-Verlag, Heidelberg, LNCS 561, 1991: 1.

[6] Kurosawa K and Sato F. A relationship between linear complexity and k-error linear complexity. IEEE Transactions on Information Theory, 2000, 46(2): 694-698.

[7] Games R A and Chan A H. A fast algorithm for determining the complexity of a binary sequence with period 2n. IEEE Transactions on Information Theory, 1983, 29(4): 144-146.

[8] Massey J, Costeuo D, and Juotesen J. Polynomial weights and code constructions. IEEE Transactions on Information Theory, 1973, IT-19(1): 101-110.

[9] 周旋, 瞿成勤, 李斌. 单圈T函数输出序列性质研究. 电子技术学院学报, 2009, 21(6): 13-16.Zhou Xuan, Qu Cheng-qin, and Li Bin. Research on properties of output sequences of single cycle T-function.Journal of Institure of Electronic Technology, 2009, 21(6):13-16.

[10] 王菊香. 周期序列的k-错线性复杂度分析和研究.[硕士论文],合肥工业大学, 2009.Wang Ju-xiang. Analyse and research of the k-error linear complexity of periodic sequences. [Master dissertation],Hefei University of Technology, 2009.

[11] 郝年朋, 岳勤. 二元周期序列线性复杂度的2位置错误谱. 计算机工程, 2010, 36(2): 158-160.Hao Nian-peng and Yue Qin. 2-position error spectrum of linear complexity for binary periodic sequence. Computer Engineering, 2010, 36(2): 158-160.

[12] Xu Li-qing. On GF(P)-linear complexities of binary sequences. The Journal of China Universities of Posts and Telecommunications, 2009, 16(4): 112-115.