习题课的探究性教学

唐锋

（常熟理工学院数学与统计学院，江苏常熟 215500）

习题课的探究性教学

唐锋

（常熟理工学院数学与统计学院，江苏常熟 215500）

探究性教学注重学生的自主学习、合作学习、开放学习，注重师生间的交互作用。探究性教学可以提高学生的学习兴趣，提高学生对知识的认知度。本文介绍在讲授微积分中值定理的习题课中如何使用探究性教学，使学生加深对该知识的理解并体会线性代数在微积分中的应用。

探究性教学；泰勒公式；罗尔中值定理；范德蒙行列式

探究性教学注重学生的自主学习、合作学习、开放学习，注重师生间的交互作用。探究性教学可以提高学生的学习兴趣，提高学生对知识的认知度。在微积分课程[1]的关于“中值定理”的习题课讲授中，笔者尝试了一次探究性教学方式，获得了意想不到的效果。下面就介绍本次习题课的情况。

首先，教师举出一个命题请学生证明，大部分学生在经过教师的细致分析后都能很快给出简洁的证明过程。

命题设f(x)在闭区间[a,b]上连续，在开区间(a,b)内存在连续的二阶导数。证明：存在c∈(a,b)，使得

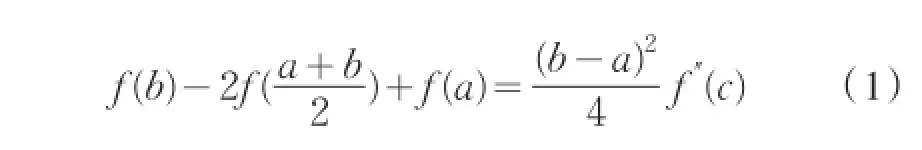
分析在关于导数的等式命题中，应该首先想到中值定理。若导数是高阶的，则应该想到利用“泰勒公式”，而“泰勒公式”又涉及到关于点的取法问题，观察到公式（1）中有一个特殊的点是区间[a,b]的中点。于是猜想应该在点处使用“泰勒公式”。

证明由泰勒公式得

提出问题1该命题的条件和泰勒中值定理的条件相类似，但命题多了“二阶导数连续”这一条件。于是自然提出多出的该条件是否必要？如不必要，定理的结论是否仍然相同？

定理1[2]设f(x)在闭区间[a,b]上连续，在开区间(a,b)内存在二阶导数。证明：存在c∈(a,b)，使

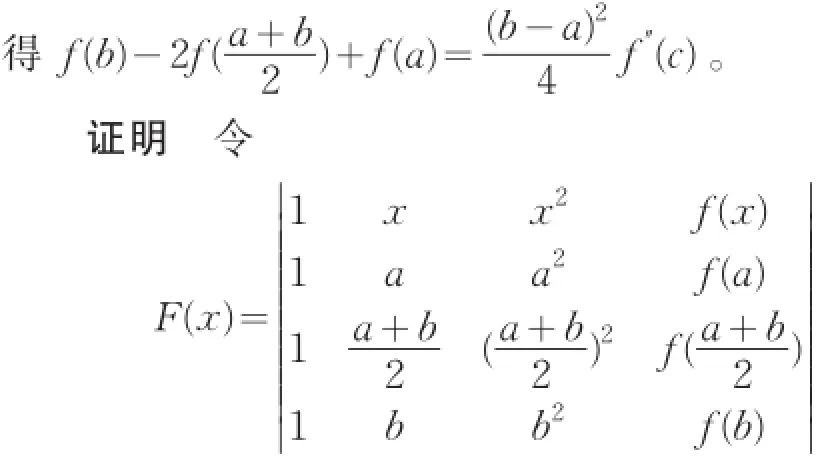
F(x)按第一行展开，可得：F(x)在[a,b]上连续，在(a,b)内存在二阶导数。又

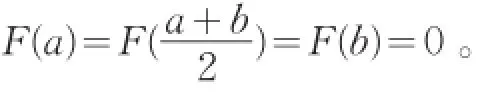
从而F′(x)在[ξ1,ξ2]上又满足罗尔中值定理的条件，故存在c∈(ξ1,ξ2)⊂(a,b)，使得F″(c)=0，但

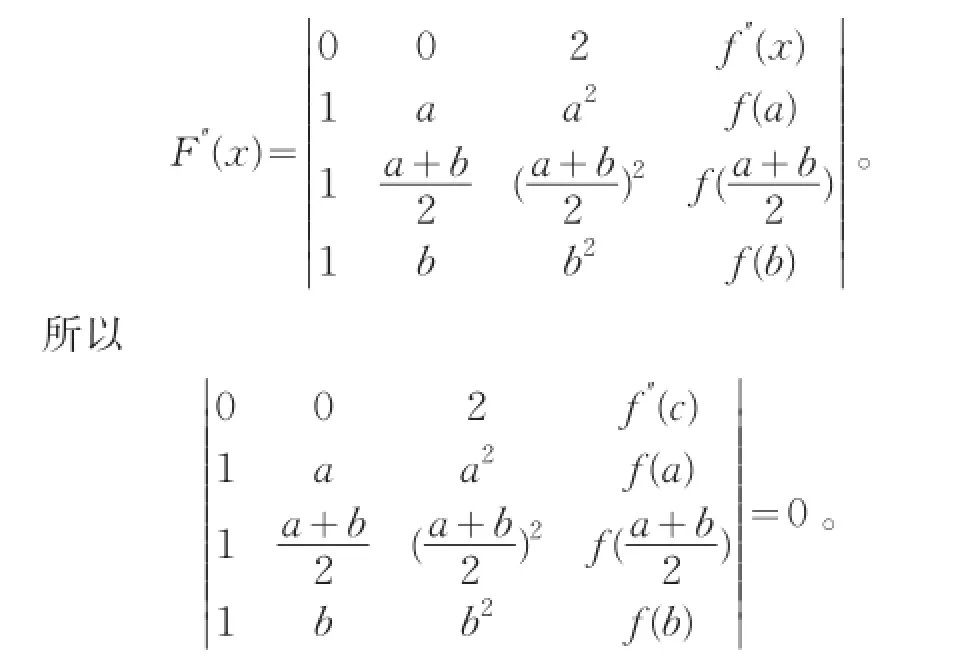
按第一行展开，得

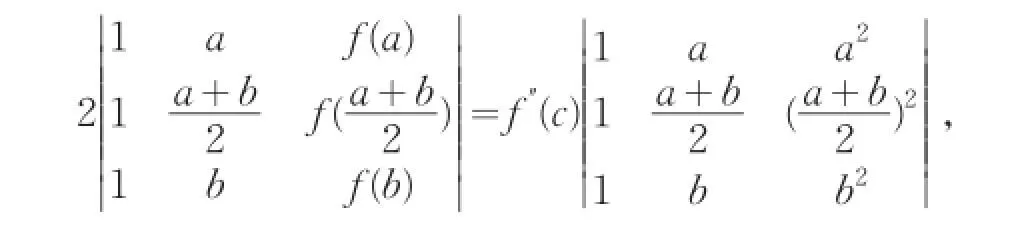
由范德蒙行列式[3]的性质可得

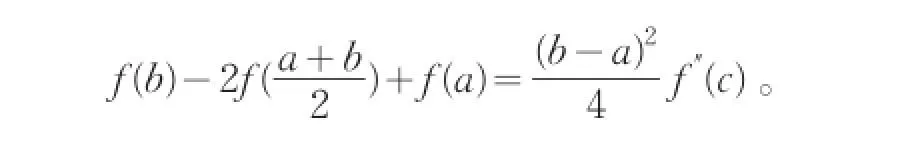
定理得证。

注1定理1证明和命题的证明相差很大，定理1不能直接照搬命题的证明，原因在于闭区间上连续函数的介值定理的条件已经不满足。学生探究的难度很大，教师应该直接给出证明。

下面是经过教师的启发，让学生对该问题继续探究，完全可以根据定理1进行推广而获得的更一般结论。过程如下：

提出问题2该定理的证明是构造了一个行列式函数，在构造的四阶行列式中，元素很特别，它是区间(a,b)的中点。于是自然提出，如果将换作(a,b)内的任意一个值x（当然，此时四阶行列式的第一行中的x应该换为别的符号），应该可以得到相应的更一般的结论，从而可以得到定理1的推广。演示如下

对于x∈(a,b)，构造函数

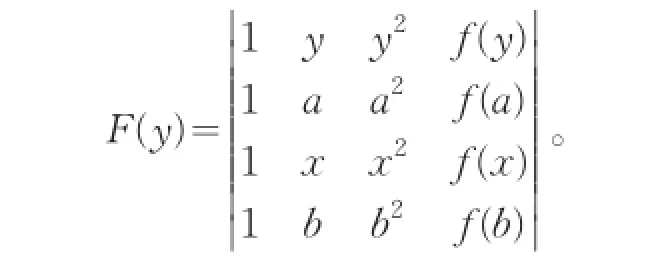
将F(y)按第一行展开，可得：F(y)在[a,b]上连续，在(a,b)内存在二阶导数。又

F(a)=F(x)=F(b)=0。

于是由罗尔中值定理，存在ξ1∈(a,x)，ξ2∈(x,b)，使得

F′(ξ1)=F′(ξ2)=0。

从而F′(y)在[ξ1,ξ2]上又满足罗尔中值定理的条件，故存在c∈(ξ1,ξ2)⊂(a,b)，使得F″(c)=0，但

由范德蒙行列式的结果可得

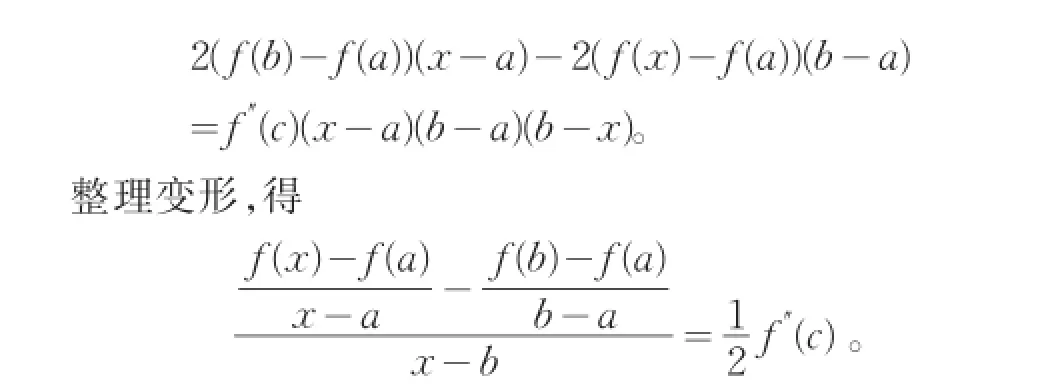
于是我们得到如下的一般性结论。

定理2[2]设f(x)在闭区间[a,b]上连续，在开区间(a,b)内存在二阶导数。证明：对于任意x∈(a,b)，存在c∈(a,b)，使得

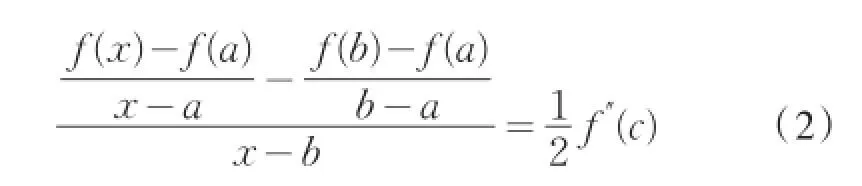
探究性教学不能在任何场合都使用，一定要因材施教。从探究的主题内容方面讲，学生一般对探究主题的生成没有前期的思想准备。但教师必须做好充分、全面的准备。命题和定理1的证明跨度较大，若让学生探究，学生会产生很大的挫折感，反而达不到学习的目的。但定理1和定理2之间的联系非常密切。在经过教师的简单提示后，学生很容易对问题探究下去，并且可以得到更加广泛的结论，这样就使得学生很有成就感，充分调动了学生的学习积极性，学生对知识的理解也更加透彻。

提出问题3（2）式等号左边为什么要表达成如此的形式？

经过简单的提示，学生回答如下：

教师继续引导学生对该问题进行探究。

提出问题4定理2中的x可以看作在(a,b)内任意插入一个点，那么将条件“插入一个点”推广为“插入两个点”如何？更一般地，“插入很多点”如何？

提示学生：在定理2的证明中，构造了函数

学生回答如下：

若“插入两个点x1＜x2”，则构造行列式函数时应该出现五个变量，即y,a,x1,x2,b，于是显然应该构造出类似的五阶行列式函数。仍然使用符号F(y)，则有

F(a)=F(x1)=F(x2)=F(b)=0。

若要连续使用罗尔中值定理，则显然应该使得F(y)在(a,b)内存在三阶导数，从而也要使得f(x)在(a,b)内存在三阶导数。“插入更多点”时依此类推。

经过以上的探讨，可以很快写出即将得到的定理的条件以及结论的最关键步骤，虽然还不知道结论到底如何表达，演示如下：

将F(y)按第一行展开，可得：F(y)在[a,b]上连续，在(a,b)内存在n-1阶导数。由行列式的性质，得

F(a)=F(x1)=F(x2)=…=F(xn)=F(b)=0，

连续使用罗尔中值定理得，存在c∈(a,b)，使得F(n-1)(c)=0，但

此行列式按第一行展开得

等号左边按照最后一列展开，再由范德蒙行列式的性质整理，即有

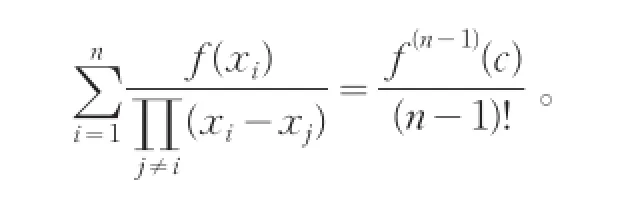
至此，经过一系列的推导，学生很快能整理出如下定理：

定理3[2]设f(x)在闭区间[a,b]上连续，在开区间(a,b)内存在n-1阶导数。证明：对于a=x1＜x2＜…＜xn=b，存在c∈(a,b)，使得

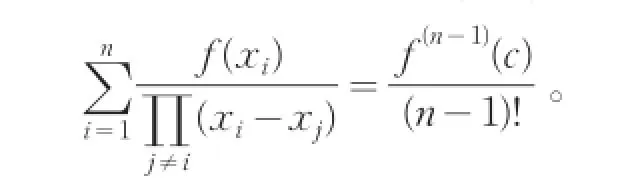
在本次的探究性教学中，教师引导学生由浅入深，由易入难，学生的学习积极性完全被调动起来，最终由学生推导出一个一般性的结论。在整个过程中，学生对于几个中值定理的理解更加深入，并且获得了一个副产品，即认识到了微积分课程与线性代数课程知识的互相渗透。完全达到了习题课的要求。

需要指出的是：在多数高校中，一般是先学习高等数学，然后是线性代数，所以上述的探究性教学基本上是不可行的。但我院的计算机科学与工程学院这两门课程同时开设，并且按照教学进度，线性代数的行列式理论是在微积分的中值定理理论之前讲授完成，所以这样的探究性教学完全可以实行。

本次探究性教学营造了一种合适的探究氛围。教师不满足于填鸭式教学，改变了教师的地位，成为学生课堂学习的指导者和帮助者，突出了学生的主体位置。教师希望学生成为问题的发现者，并激励学生实际参与解决问题。但是，在探究式教学中，教师也不应成为陪衬者，应该要有交互活动，师生都应该是课堂教学的主体。必须强调：教师的指导要求“准确”、“适当”、“有效”。教师一定要认识到，虽然一次课可能完成一个主题的探究，但不是每一个主题都能在一次课内探究出结果。另外，探究性教学不能尝试太多，否则，学生会感觉太累，会逐渐害怕高数的学习，从而丧失学习的主动性。

［1］同济大学应用数学系.高等数学［M］.第五版.北京：高等教育出版社，2007：126-143．

［2］樊恽，郑延履，刘合国.线性代数学习指导［M］.北京：科学出版社，2003：377-386．

［3］同济大学数学系.线性代数［M］.第五版.北京：高等教育出版社，2007：1-21．

One Prob lem Solving Lesson w ith Exp loring

TANG Feng
(School of Mathematics and Statistics,Changshu Institute of Technology,Changshu 215500,China)

Teaching through inquiry emphasizes students'self-learning,cooperative learning,and open-learning, and highlights teacher-students'interactions in classrooms.Thismethod can stimulate students'learning interest, and improve their cognitive abilities.In this paper,this method is used to teach mean value theorem in problem solving lessons.Teaching through inquiry could improve students'understanding of mathematics know ledge and making sense of how to apply linear algebra to calculus.

teaching through inquiry;Tailor formula;Rollemean value theorem;Vandermonde determinant

O172，G424.21

A

1008-2794（2011）06-0093-04

2010-08-30

唐锋(1973—)，男，江苏泰兴人，常熟理工学院数学与统计学院讲师，硕士，主要研究方向为有限群论。