《机械原理》中四杆机构的运动分析

赵连生

（常熟理工学院机械工程学院，江苏常熟 215500）

《机械原理》中四杆机构的运动分析

赵连生

（常熟理工学院机械工程学院，江苏常熟 215500）

针对学生学习《机械原理》课程中运动分析的困惑，本文给出了低副要素的运动特点、参考点的选择、哥氏加速度存在的条件，并举例作了相应的运动分析，以提高学生对机构运动分析的分析能力和课堂教学效果。

机械原理；运动分析；四杆机构

《机械原理》对于机械工程类专业来说，是一门专业基础课，也是一门学位课程，知识结构承前启后，是学习专业课的基础。在《机械原理》教学中，平面机构的运动分析是必不可少的教学内容。虽然学生在《理论力学》教学过程中已经学过了相关的运动分析，但普遍掌握得不够扎实，针对实际机构的运动分析往往无从下手。如选择哪两点列运动矢量方程？何时会有哥氏加速度存在？学生对此时常会感到困惑。本文就此问题，结合《机械原理》课程的实际教学情况，针对四杆机构的运动分析总结了几点体会。

一、低副要素的运动特点

经过高副低代后，任何平面机构都可以认为是由低副连接而成的。因此，在进行平面机构运动分析时，必须明确组成低副的两构件之间相对运动的特点。

转动副：若构件2、3在B点组成转动副，则构件2上的B2点和构件3上的B3点之间不可能产生任何的相对移动，所以这两点具有相同的速度和加速度，即VB2=VB3=VB，aB2=aB3=aB。

移动副：若构件2、3组成移动副，则构件2和构件3之间不可能产生相对转动，所以这两构件具有相同的角速度和角加速度，即ω2=ω3，ε2=ε3。

二、参考点的选择

在《理论力学》中明确给出了动点系的选择原则：动点系之间必须有相对运动，相对运动轨迹是已知曲线［1］。而针对实际机构，参考点的选择并不像《理论力学》中的运动分析那么复杂。

首先，根据运动分析给出的已知条件，确定已知点。所谓已知点，是指该点的速度和加速度可由已知条件直接求得。一般情况下，机构运动分析都给出了机构的结构尺寸和曲柄的角速度及角加速度，所以曲柄端点的速度和加速度可以直接求得，故曲柄端点往往就是已知点。

其次，根据机构的组成情况和所要求解的内容，合理选择另一点，并列出两点间的矢量方程进行求解。可分为两种情况：

1）选择同一构件上的两点列矢量方程。这一构件通常是四杆机构中的连杆，而两个点一般为连杆上两个转动副对应的点。此方案常用于铰链四杆机构、曲柄滑块机构和移动导杆机构的运动分析。

2）选择组成移动副两构件上的重合点列矢量方程。这个重合点就是已知点的位置，此方案常用于曲柄摇块机构、曲柄转块机构、摆动导杆机构和转动导杆机构的运动分析。

三、哥氏加速度存在的条件

在四杆机构的加速度运动分析时，若选择组成移动副两构件上的重合点列矢量方程，则在加速度矢量方程中一定存在哥氏加速度。其大小为akB3B2=2ω2× VB3B2，注意下标先后次序表示的含义，其角速度和相对速度的大小及方向由速度分析求得。

四、举例

（一）曲柄滑块机构的运动分析

图1a）所示为一曲柄滑块机构，已知：曲柄1长度为lAB=50mm，连杆2长度为lBC=150mm，θ=45°，曲柄以ω1=10 rad/s顺时针匀速转动，求滑块3的速度VC和加速度aC。

分析：对于曲柄滑块机构，由于组成移动副的一个构件（导杆）为机架，故此机构在运动分析中不存在哥氏加速度。由题意知已知点为B点，所以选择同一构件（连杆）上的B、C两点列矢量方程进行求解。

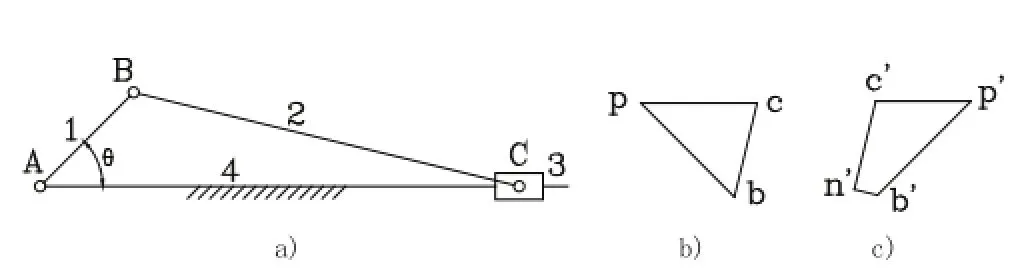
图1 曲柄滑块机构的运动分析

aC=μa×p'c'=0.1×36=3.6m/s2（方向：p'→c'）。

（二）曲柄摇块机构的运动分析

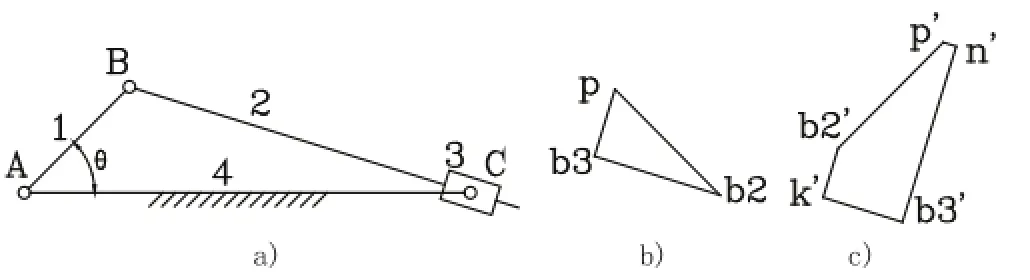
图2 曲柄摇块机构的运动分析

图2 a)所示为一曲柄摇块机构，已知曲柄1长度为lAB=50mm，机架4长度为lAC=150mm，θ=45°，曲柄以=10 rad/s顺时针匀速转动，求滑块3的角速度ω3和角加速度ε3。

分析：由题意知，此曲柄摇块机构的已知点为B点。学生往往会选择同一构件（杆2）上B、C两点去列矢量方程：

VC2=VB2+VC2B2

大小：？ω1lAB？

方向：？⊥AB⊥BC

由于上述矢量方程存在三个未知量，故无法求解。所以正确的求解方法应该是：选择组成移动副的构件2和构件3上的重合点列矢量方程。由于已知点为B点，所以重合点选为B点。学生可能直观地认为构件3和构件2没在B点重合，不能列运动方程。但根据机构运动简图的画法，我们知道构件的尺寸是可以无限扩大的，为此可以把构件3的尺寸扩大到B点，这样就可以在B2、B3点间列出运动方程。由于组成移动副的两个构件都是活动构件，在加速度分析时有哥氏加速度存在。

解：取机构比例尺μl=1mm/mm作机构图,如图2 a)所示，lBC=μl×BC=120mm。

1）速度分析

VB3=VB2+VB3B2

大小：？ω1lAB？

方向：⊥BC⊥AB∥BC

VB2=ω1lAB=10×0.05=0.5m/s，取速度比例尺μV=0.01 (m/s)/mm，作速度图，如图2b)所示。则

VB3=μV×pb3=0.01×23.4=0.234m/s（方向：p→b3），

VB3B2=μV×b2b3=0.01×44.2=0.442m/s（方向：b2→b3），

ω2=ω3=VB3/lBC=0.234/0.12=1.95rad/s（方向：逆时针）。

2）加速度分析

解：取机构比例尺μl=1mm/mm作机构图,如图1 a）所示。

1）速度分析

VC=VB+VCB

大小：？ω1lAB？

方向：∥AC⊥AB⊥BC

VB=ω1lAB=10×0.05=0.5m/s，取速度比例尺μV=0.01 (m/s)/mm，作速度图，如图1b)所示。则

VC=μV×pc=0.01×49.9=0.499m/s(方向：p→c)，

VCB=μV×bc=0.01×36.4=0.364m/s(方向：b→c)，

ω2=VCB/lBC=0.364/0.15=2.43rad/s(方向：逆时针)。

2）加速度分析

aC=aB+anCB+atCB

大小：？ω21lABω22lBC？

方向：∥AC B→A C→B⊥BC

aB=ω2

1lAB=102×0.05=5m/s2，anCB=ω2

2lBC=2.432× 0.15=0.9m/s2，取加速度比例尺μa=0.1(m/s2)/mm，作加速度图，如图1c)所示。则

anB3+atB3=aB2+akB3B2+arB3B2

大小：ω23lBC？ω21lAB2ω2VB3B2？

方向：B→C⊥BC B→A⊥BC∥BC

aB=ω21lAB=102×0.05=5m/s2,anB3=ω23lBC=1.952×0.12= 0.456m/s2，akB3B2=2ω2VB3B2=2×1.95×0.442=1.72m/s2，取加速度比例尺μa=0.1(m/s2)/mm，作加速度图，如图2c)所示。则

ε2=ε3=atB3/lBC=μa×n'b3'/lBC=0.1×61.4/0.12=51.2 rad/s2（方向：逆时针）。

五、小结

平面机构的运动分析是《机械原理》课程的重点教学内容，也是一个教学难点，学习时必须牢记低副要素的运动特点。对于平面四杆机构来说，若组成移动副的两个构件都是活动构件，则选择这两个构件的重合点列矢量方程求解，且一定存在哥氏加速度；除此之外就选择同一构件（连杆）上两个点列矢量方程求解，且一定不存在哥氏加速度。

［1］沈晓阳，王平.理论力学和机械原理课程运动合成的异同分析［J］.高等函授学报，2010（10）：35-37.

Teach ing Experience of“M echanical Princip le”in k inem atic analysis

ZHAO Lian-sheng
(School of Mechanical Engineering,Changshu Institute of Technology,Changshu 215500,China)

The paper seeks to solve the confusion of students when they learn kinematic analysis in the course of“Mechanical Principle”.Motion characteristics of the elements of lower-pairs,the choice of reference point,the existence terms of Coriolis acceleration,and the examples of the appropriate kinematic analysis are presented to improve the students'skills of kinematic analysis and effect of classroom teaching.

mechanical princip le;kinematic analysis;four poles organizations

G642

A

1008-2794（2011）06-0115-03

2011-03-10

赵连生（1962—），男，江苏常熟人，常熟理工学院机械工程学院副教授，主要研究方向为机械设计及理论。