家电理论报废量静态预测模型建立及分析

□文/郑骥 徐祥阳

北京机电院高技术股份有限公司

自上世纪80年代开始，电视机、洗衣机等家用电器开始大规模进入人们生活中。随后，这些家电也开始逐渐进入报废期。2009年之前，我国的废旧家电大多由非正规商贩收走，收走的废旧家电或被简单翻新后流入农村，或者由家庭作坊简单拆解提取金属、线路板等有价值成分后随意丢弃剩余部分。废旧家电报废、回收、拆解行业整体发展无序；具体回收报废量也无从得知。2009年6月1日，国务院办公厅颁布了家电以旧换新活动实施方案，决定在北京、天津等9省市进行家电以旧换新试点工作，随后又在全国大范围推广实施该政策。家电以旧换新政策有效规范了我国废旧家电报废回收渠道。据商务部统计，截至2011年3月7日，全国参与家电以旧换新活动回收的废旧家电多达4171.9万台。

家电报废量预测对于行业主管部门制定产业政策和企业在该领域项目投资决策具有重要意义。然而，由于缺乏公开的基础数据和入户统计工作难度大，目前家电报废量预测模型相关研究较少。中国家用电器研究院何逸林等在研究我国家用电器理论报废量时，构建了基于家电销售量、家电社会保有量年增加量和家电社会保有量系数法三种模型来估算理论报废量。Axion公司在开展伦敦电子废弃物流通研究时，则利用地区人口统计数据、家庭电器拥有率、使用年限作为主要参数，基于实地收集的大量数据测算了伦敦家用电器报废量。可惜的是，当时尚无回收报废量实际数值，因此这些模型只提供了预测值，无法进行模型预测效果评估。随着我国家电以旧换新政策实施和报废家电回收数据的公布，使得评价和完善已有预测模型以及建立新模型成为可能。

本文基于我国家电“以旧换新”活动中收回的废旧家电数据，建立了理论报废量预测模型。模型建立过程中仅考虑家电中的电视机、洗衣机、电冰箱、空调和电脑，即家电以旧换新活动涉及到的五种家电，且只对总的家电报废量预测，不考虑不同种类家电的报废情况。建立的模型为静态模型，不考虑回收量与时间的变化关系。

一、模型建立

模型1：基于人口统计学数据测算。

模型2：基于家电保有量测算。保有量按照各地区统计年鉴公布的城镇、农村居民家庭年末耐用品百户拥有量和城镇、农村家庭总户数来计算。

模型3：基于家电保有量与地区人均GDP乘积测算。

所有模型均采用一元线性方程模拟测算，用y=ax表示，其中y为预测理论报废量；x为自变量，不同模型将选用不同数据；a为拟合得到的回归系数。

回归系数a使用国家环保部公布的家电以旧换新首批试点省市2009年8月至2010年5月间回收数据作为自变量（如表1所示），采用一元线性回归法拟合得到；由于该数据为10个月内的回收量，拟合过程中将原数据乘以1.2转换成12个月数据后再行使用。

表1 环保部公布首批试点省市家电回收量（单位：万台）

一元线性回归法拟合使用Microsoft Excel®软件完成。针对拟合得到的各个一元线性方程计算了置信度为90%时的置信区间。

表2 家电报废量预测模型方程

二、结果及讨论

表2给出了三个模型拟合计算得到的回归系数、复相关系数和置信区间。其中，模型1选择第六次人口普查公布的地区常住人口作为自变量；模型2选择计算得到的2000年各地区家电保有量作为自变量；模型3选择计算得到的2000年各地区家电保有量与2010年人均GDP值二者乘积作为自变量。复相关系数越接近1，表明自变量之间线性关系越好，也表明模型预测效果越好。置信区间数值则代表了预测值有90%的概率落在该误差范围内。图1给出了三个模型的拟合效果。

图1 三个模型预测效果

1.三种模型比较

从数据易获得性方面来看，利用当地常住人口数进行家电报废量估算最为容易，然而这个模型的复相关系数仅为0.21，预测结果可信度较低，建议仅作为粗略范围估算时用。从相关性上来看，基于家电保有量或者家电保有量与地区人均GDP乘积的两个模型变量之间已经具有明显的线性关系，预测结果均具有较好可信度，都可用于进行理论报废量预测，其中模型3的复相关系数达到0.82，是三个模型中预测准确度最高的。不过，由于各个地区通常并不直接统计家电保有量数据，需要利用地区统计年鉴收录的年末耐用品百户拥有量和家庭总户数数据推算出来，这给模型2和模型3的应用带来一些额外工作量。

2.保有量与人均GDP对应年代的选择

根据我国《家用电器安全使用年限细则》规定，不同家用电器安全使用年限不同，例如电冰箱为12～16年、电视机为8～10年、个人电脑为6年，因此模型测算过程中选择不同年代的保有量数据对预测结果可能会有一定影响。类似地，人均GDP也存在年代选取问题。表3和表4给出了选择不同年代的家电保有量和人均GDP进行线性拟合后的结果。

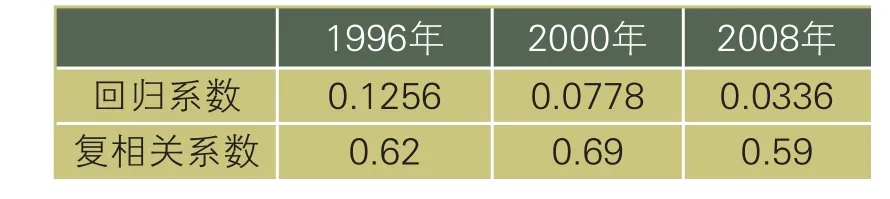
表3 基于不同年代家电保有量的预测模型

表4 基于不同年代人均GDP的预测模型

由表3可见，利用2000年家电保有量数据拟合效果最好。实际上，各个地区回收上来的废旧家电80%左右为电视机，而电视机安全使用年限为10年，这似乎与拟合结果相吻合，然而，鉴于表3中的复相关系数之间并没有太大的差别，也没有实际回收上来废旧电器使用年限的具体数据，因此还需要更多的研究来证实这一点。

比较表4中的不同年代人均GDP对应的复相关系数可见，2010年对应的人均GDP数据拟合效果均优于利用当年数据拟合效果。这给模型应用带来一定便利，因为当前的统计数据通常更容易获得一些。

综合表3和表4结果，建议实际测算过程中采用最容易获得的数据进行估算，如有可能，保有量数据可选择预测年往前倒退十年左右的数据，如本文选择十年前的2000年的数据，而人均GDP则尽可能选择当前最新数据。

3.政策效应

由于家电以旧换新活动实施的补贴力度非常大，大家更愿意把废旧家电以以旧换新的形式交给正规回收渠道，试点省市的家电回收量总量都相当巨大，政策的促进效应十分明显。然而，与对应的家电保有量相比，有些地区实际回收量偏高，有些地区则偏低。

图2 校正系数对政策效应的反映

地区经济发达程度、政策执行规范程度、参与以旧换新活动网点数量及分布、下游拆解企业处理能力等诸多因素都可能会在短期内影响到政策的实施效应。不同地区的政策效应有所不同，一定程度上会造成用预测模型估算的家电理论报废量与实际报废量之间出现较大偏差。反之，预测的家电理论报废量与实际报废量之间出现的偏差也可以一定程度上反映这种政策实施效应。

通过对自变量数据进行系数校正，将能提高模型的预测效果。例如，模型3相当于利用各个地区人均GDP对家电保有量数据进行校正，拟合效果与模型2相比即有了明显改善。对模型3中预测值与实际值偏差较大的几个点进行了单独的系数校正。设定北京和广东两地实际回收量应放大40%，而上海实际回收量应缩减40%，进行校正后再次拟合，复相关系数由0.80提高到0.98，拟合效果对比如图2所示。拟合使用的家电保有量为2008年数据，人均GDP为2010年数据。

然而，目前这些校正系数的设定带有很大的主观意识。随着家电以旧换新政策的长期规范执行和公布的基础数据更详细更全面，不同地区政策效应应可通过相关数据计算出来。

三、结论

1.基于常住人口的预测模型数据最易于获得，但拟合相关性较低，适合于粗略范围估算。基于家电保有量或者家电保有量与地区人均GDP乘积的两个模型变量之间已经具有明显的线性关系，均可用于测算理论报废量。

2.在建立的三个模型中，选择十年前家电保有量和当前人均GDP数据进行一元线性拟合，相关性最高，预测效果最好。

3.家电以旧换新活动有着明显的短期政策效应，使得部分地区回收量相对放大或者缩小。