矩阵和关于{1,2}-逆与{1,3}-逆的混合吸收律
李 莹, 高 岩
(1.上海理工大学管理学院,上海 200093;2.聊城大学数学科学学院,聊城 252059)
1 预备知识
以Cm×n表示所有m×n复矩阵的集合.A*,A-1, r(A),R(A)分别表示矩阵A的共轭转置、逆矩阵、秩、值域.给定矩阵A∈Cm×n,其广义逆[1,2]是满足下列4个方程中某些方程的矩阵G:a.AG A=A;b.GA G =G;c.(AG)*=AG;d.(GA)*=GA.
令Ø≠η={i,j,k}⊆{1,2,3,4},用Aη表示满足以上4个方程中的(i),(j),(k)方程的矩阵G的集合,Aη中的任何一个矩阵G称之为矩阵A的一个{i,j,k}-逆,记为A(i,j,k).若η={1,2,3,4},则称G为A的M-P逆,记为A+.EA=I-A A+,FA =I-A+A分别为A*,A的零空间上的正交投影.
矩阵的各种类型的广义逆在实际中都有广泛的应用.它们在概率统计、数学规划、控制论、测量学、博弈论及网络理论等领域都有极其重要的作用[3].同时在研究最小二乘问题、长方及病态线性方程问题及马尔可夫链等统计问题中也是一种基本的工具.广义逆应用的广泛性要求其自身理论发展不断地充实和完善.
如果A,B为非奇异矩阵,则A-1+B-1=A-1(A +B)B-1总是成立的,但对于广义逆矩阵,文献[4]中举例说明了不一定存在A(1),B(1),使得A(1)+B(1)=A(1)(A+B)B(1),并推导了关于上式成立的充要条件.本文考虑将其中的两处逆矩阵换成两种不同的{i,j,k}-逆矩阵,若仍有等式成立,则称两矩阵和关于两个广义逆满足混合吸收律,现分别给出混合第一、第二吸收律的概念.
定义1 设A,B∈Cm×n,如果存在G∈Aη,H∈Bζ使得A(G+H)B=A+B,则称A,B关于η-逆和ζ-逆满足混合第一吸收律.
定义2 设A,B∈Cm×n,如果存在G∈Aη,H∈Bζ使得G+H=G(A+B)H,则称A,B关于η-逆和ζ-逆满足混合第二吸收律.
若η=ζ,则定义1和定义2为矩阵和关于某一种广义逆的第一、第二吸收律.
在文献[5-12]中,作者提出了一种矩阵秩方法.近年来,该方法作为矩阵研究的一个有力工具越来越受到重视,并被大量应用到广义逆矩阵、矩阵方程、矩阵不等式、反序律、正序律、最小二乘以及统计量分析等问题的研究中[13-16].该方法的运用将这些问题的研究推到了一个新的层面.矩阵秩方法的主要思想是将矩阵等式问题转化成秩的问题去解决.这看似简单的转化事实上富有深刻的思想内涵,它将复杂的矩阵表达式的问题归结为简单的数字指标——秩,刻画了一些以往的方法无力解决的问题.本文拟用矩阵秩方法与广义Schur补结合矩阵的奇异值分解(SVD)对本文所定义的两个矩阵和关于广义逆的混合吸收律进行研究,通过推导某些矩阵表达式的极大、极小秩(简称极秩)获得两个矩阵和关于{1,2}-逆与{1,3}-逆的混合第一、第二吸收律成立的充要条件.
引理1[9]设A∈Cm×n,B∈Cm×k,C∈Cl×n, D∈Cl×k,则


引理2[10]设A∈Cm×n,B∈Cm×k,C∈Cl×n, D∈Cl×k.则

其中

引理3[17]设A∈Cm×n,B∈Cm×k,C∈Cl×n.则有

引理4[17]设A∈Cm×n,B∈Cm×k,C∈Cl×n.若R(AQ)=R(A),R((PA)*)=R(A*).则

2 矩阵和关于{1,2}-逆与{1,3}-逆的混合第一吸收律
定理1 设A,B∈Cm×n,则

证明 由式(6)

利用式(4)对其中的极秩

进行计算.


而



因而

定理2 设A,B∈Cm×n,则

证明

根据式(5)计算

其中

所以


从而
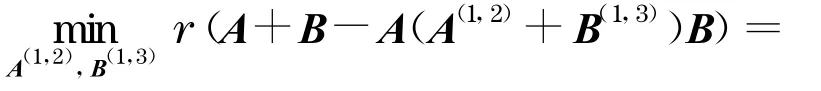

现分别利用式(7)和式(8)结合引理4计算上式中的两个极秩.

因此


从而

推论1 设A,B∈Cm×n,则下列叙述等价.
a.任意A(1,2)∈A{1,2},B(1,3)∈B{1,3}都有A+B=A(A(1,2)+B(1,3))B.
b.存在A(1,2)∈A{1,2},B(1,3)∈B{1,3}使得A+B=A(A(1,2)+B(1,3))B.


3 矩阵和关于{1,2}-逆与{1,3}-逆的混合第二吸收律
定理3 设A,B∈Cm×n,则

证明 由式(4)

推论2 任意A(1,2)∈A{1,2},B(1,3)∈B{1,3}都有A(1,2)+B(1,3)=A(1,2)(A+B)B(1,3),当且仅当A,B为非奇异阵.
定理4 设A,B∈Cm×n,则

证明 由式(6)


从而



现分别计算两个极秩.由于P*为行满秩阵,而右乘行满秩阵,秩不发生变化,所以,由式(3)

又由式(4)

所以

现考虑其中的r(B*P1).由A的奇异值分解知从而

所以

故结论成立.
推论3 存在A(1,2)∈A{1,2},B(1,3)∈B{1,3}使得A(1,2)+B(1,3)=A(1,2)(A+B)B(1,3)当且仅当

证明 存在A(1,2)∈A{1,2},B(1,3)∈B{1,3}使得A(1,2)+B(1,3)=A(1,2)(A+B)B(1,3),当且仅当

若r(A)≥r(B),则有r(B*P1)=r(A),而r(B*P1)≤r(B),所以r(B*P1)=r(A)=r(B).
若r(A)≤r(B),则有r(B*P1)=r(B),而r(B*P1)=r(B*AA+B)≤r(A),所以r(B*P1)= r(A)=r(B).故结论成立.
文献[4]中给出了存在A(1)∈A{1},B(1)∈B{1}使得A(1)+B(1)=A(1)(A+B)B(1)成立的等价条件,即r(A)=r(B),此处对于A(1,2),B(1,3)而言,显然,条件有别于A(1),B(1).可以得到如下结论:若存在A(1,2),B(1,3)使得混合第二吸收律成立,则关于A(1), B(1)的第二吸收律必成立;反之,则不一定.
4 结束语
本文中仅考虑了两个矩阵和关于{1,2}-逆与{1, 3}-逆的混合第一、第二吸收律成立的充要条件,用同样方法可以考察其他类型的广义逆的混合吸收律,并对其结果进行横向比较.另外,在本文中每一个吸收律等式中所涉及的某种广义逆均为同一个广义逆矩阵;若不同,则问题转化为考察关于矩阵及其广义逆的表达式构成的两个集合之间的关系,此时问题将复杂得多,这也是作者下一步将要研究的课题.
[1] BEN-ISRAEL A,GREVILLE T N E.Generalized Inverses:Theory and Applications[M].New York:John Wiley&Sons,1974.
[2] 郭文彬,魏木生.奇异值分解及其在广义逆理论中的应用[M].北京:科学出版社,2008.
[3] 王松桂,杨振海.广义逆矩阵及其应用[M].北京:北京工业大学出版社,1996.
[4] 陈孝娟,郭文彬.奇异值分解在广义逆中的应用[J].华东师范大学学报(自然科学版),2008,1:25-29.
[5] TIAN Yongge.Reverse order laws for the generalized inverses of multiple matrix products[J].Linear Algebra and its Applications,1994,211(1):85-100.
[6] TIAN Yongge,GEORGE P H.Styan.Rank equalities for idempotent and involutary matrices[J].Linear Algebra and its Applications,2001,335(1/2/3):101-117.
[7] TIAN Yongge.The Moore-penrose inverse of a partitioned matrix and its applications[J].Appl Math J Chinese University,1992,7:310-314.
[8] TIAN Yongge.Calculating formulas for the ranks of submatrices in the moore-penrose inverse of a matrix [J].J Beijing Polytechnical University,1992,18: 84-92.
[9] TIAN Y,STYAN G P H.ON some matrix equalities for generalized inverses with applications[J].Linear Algebra and its Applications,2009,4309(10):2716-2733.
[10] TIAN Yongge.More on maximal and minimal ranks of Schur complements with applications[J].Appl Math Comput,2004,152(3):675-692.
[11] TIAN Yongge,LIU Yonghui.Extremal ranks of some symmetric matrix expressions with applications[J]. SIAM J M atrix Anal Appl,2006,28(3):890-905.
[12] MARSAGLIA G,STYAN G P H.Equalities and inequalities for ranks of matrices[J].Linear and Multilinear Algebra,1974,2(3):269-292.
[13] GUO Wenbin,WEI Musheng,ZHAO Jianli.Forward order law for g-inverses of the product of two matrices[J].Applied Mathematics and Computation,2007, 189(2):1749-1754.
[14] GUO Wenbin,WEI Musheng,WANG Minghui.On least squares g-inverses and minimum norm g-inverses of a bordered matrix[J].Linear Algebra and its Applications,2006,416(2/3):627-642.
[15] LIU Yonghui,WEI Musheng.Rank equalities related to the generalized inversesof two matrices A and B[J].Applied Mathematics and Computation,2004,159(1):19-28.
[16] LIU Yonghui,WEIMusheng.Rank equalities for submatrices in generalized inverseof M[J].Applied Mathematics and Computation,2004,152(2): 499-504.
[17] HU D.The general solution to the matrix equation AXB+CYD=E[J].Math Practice Theory,1992,4: 85-87.

