自组织理论的概念、方法和应用

许立达, 樊 瑛, 狄增如

(北京师范大学管理学院,北京 100875;北京师范大学复杂性研究中心,北京 100875)

人类在对物质的微观结构、基本粒子之间的相互作用以及天体运动和宇宙演化等问题获得深刻的科学认识后,宏观领域的复杂性问题成为学术界关注的主题.宏观层次最接近我们熟悉的生存环境,时空尺度在米和秒的范围内,涉及自然科学和社会科学等多个领域.这一空间尺度最突出的特点是系统的多样性与复杂性,引起人们关注的基本问题是:在这些纷繁复杂的结构与运动形式背后,有没有核心的科学问题和普适的基本规律,热力学和统计物理学在远离平衡的非线性区所取得的成果,为理解自然和社会演化的基本规律做出了突出的贡献,自组织理论是其中的核心内容.

复杂系统涵盖了物理、化学、生物、社会及经济等各个领域,它的基本特点是系统中包含大量的基本单元,并且随着时间的演化,在更高的层次上不断涌现出新的结构和功能.如何认识从无序到有序的演化问题是探索生命奥秘的基本问题.经典力学所描述的物理过程都是时间反演对称的,过程可逆即不存在“时间箭头”.而热力学与统计物理学研究由大量粒子组成的系统,特别是与热现象有关的物理过程,其中我们随处可以观察到不可逆的时间演化进程,相关规律被总结为热力学第二定律,给出了系统热运动的“时间箭头”.

但热力学第二定律要求一个孤立系统要朝均匀、简单、消除差别的方向发展,这实际上是趋于低级运动形式的退化.然而,在现实生活中,我们还能观察到与之相反的演化方向,即由简单到复杂,由低级到高级,由无功能到有功能的方向演化,生命的产生和演化以及人类社会的发展是最典型的代表.两种“时间箭头”的指向问题构成了物理学、化学等研究无生命的科学与生物学、社会学等研究生命的科学的一个基本矛盾.自组织理论正是在探讨这些根本性的问题中产生的.

事实上,在物理、化学领域同样可以观察到由无序到有序的进化现象,观察到结构和功能的涌现,贝纳得(Benard)对流、激光和贝洛索夫-萨波金斯基反应(B-Z反应)是其中典型的例子,它们都是系统在某些外在条件下,自发地产生出宏观有序结构,与生命现象具有共同的特点.研究各领域中自组织现象的共性与规律,并利用相应的概念和方法研究具体系统的自组织行为,是自组织理论研究的主要问题.

自组织理论的产生和发展归功于许多在不同领域工作的科学家的贡献.其中,由比利时自由大学Prigogine教授创建的布鲁塞尔学派建立的耗散结构理论[1-4],和联邦德国斯图加特大学Haken教授所在的斯图加特学派创立的协同学[5-7],共同构成了自组织理论的核心内容,并开辟了探索复杂性问题这一科学研究的新领域[8-9],为研究“低级、简单”的物理系统与“高级、复杂”的生命系统演化提供了统一的理论基础.

本文试图对自组织理论的基本概念、研究方法以及应用作一个初步的介绍.由于近几十年发展迅速的复杂性研究都可以算作自组织理论的延伸和发展,覆盖众多的领域和问题,难以深入展开,本文将重点放在具有共性的概念和方法上,介绍自组织理论的热力学基础和研究方法,包括确定性的动力学方法、考虑微观涨落的随机性方法和自底向上的多个体模拟方法,介绍耗散结构形成的基本过程和研究自组织行为的概念方法,然后以可激发介质中的螺旋波这一典型的时空有序结构为案例,介绍自组织理论研究复杂系统的基本线路,最后,将对自组织理论的拓展和应用作概略的介绍.

1 自组织理论的热力学基础和研究方法

复杂系统研究的主要内容是研究那些由大量个体组成的宏观体系的基本性质.它主要包括以下3个方面:建立描述宏观体系的概念或参量;刻画体系所呈现的本质特性和演化规律特别是涌现性行为;探讨这些宏观层次上的性质和规律与微观层次上个体行为之间的关系.

1.1 系统的状态和状态演化

在热力学与统计物理中,由大量基本结构单元组成的宏观对象称之为热力学系统(简称为系统).与系统相互作用着的外界称为系统的环境.可以根据与外界环境相互作用的不同将系统分为孤立系统、封闭系统和开放系统3类.系统在总体上会表现出一定的宏观性质或宏观物理过程,即系统的宏观状态.把孤立系统所达到的不再随时间变化的状态称为热力学平衡态或简称平衡态;否则称为非平衡态.系统从非平衡态过渡到平衡态的过程称为驰豫过程.平衡态是研究系统性质的出发点.孤立系统到达平衡态后,系统内部不再有宏观物理过程发生,微观粒子不显现出任何宏观有序的运动.与非平衡态相比,平衡时系统内部微观粒子的运动是最无序、最无规则的.封闭系统和开放系统则可以看成是从一个大的孤立系统中划分出来的一部分,其余部分就是它的环境.若整个孤立系统处于平衡态,则作为其一部分的封闭系统或开放系统当然也就处于平衡态.

人们引入了众多的物理量来描述系统的宏观状态,分为广延量和强度量两种.广延量是系统特征大小的函数,如体积V、质量M等;强度量则与系统大小无关,如温度T、压强P、密度ρ等.由系统状态唯一确定的宏观物理性质,称之为态函数.处于非平衡态的系统,内部各处的宏观性质不同且随时间变化,在离平衡态不太远时,可以使用局域平衡假设:把系统分成许多可以看作平衡态的小部分,此时所有热力学变量都是与空间分布有关的点函数,整个系统的广延物理量则可以看作是每一小部分相应物理量的总合.

在外界作用下,系统的热力学状态随时间的变化称为热力学过程.如果在热力学过程中的每一个中间态都是平衡态,这种过程叫做准静态过程,准静态过程是对实际过程的抽象与近似.系统状态的变化需要满足一定的物理规律,人们把它总结为热力学第一和第二定律.热力学第一定律要求系统状态的变化过程要满足能量守恒.在准静态过程的一个元过程中,令δ A表示系统对外界做的功,δ Q表示外界传给系统的热量,dU表示系统内能的变化,则热力学第一定律可表示为

热力学第一定律是能量守恒和转化定律在涉及热现象的宏观过程中的具体体现.

然而并不是满足热力学第一定律的过程就一定能自发实现.系统演化的热力学过程分为两类,可逆过程和不可逆过程.对于一个热力学过程,如果存在另一过程能使系统和外界完全复原,则称之为可逆过程,只有无摩擦等耗散现象的准静态过程才是可逆过程,是一种理想抽象.事实上,涉及热现象有关的实际过程都具有方向性,是不可逆过程,一经发生,则用任何方法都不可能使系统和环境完全复原.由此经验总结,学者们建立了热力学第二定律.克劳修斯1850年将其表述为:不可能把热量从低温物体传到高温物体而不引起其他变化.1851年开尔文提出了另一种表述:不可能从单一热源吸收热量,使之完全变为有用的功而不产生其他影响.利用热力学第一定律可以证明这两种表述是等价的.

热力学第二定律可以通过引入态函数熵S来定量刻画,它是一个广延的、可加的物理量.引入熵后,可以建立包含热力学第一和第二定律的基本热力学方程

对于孤立系统,系统和环境没有能量和热量交换,δ Q=0,有

式(3)称为熵增加原理:在孤立系统中,不可逆过程总是朝着熵增加的方向进行的.它是热力学第二定律的直接结果.系统达到平衡态时,熵就达到了极大值.在统计物理学中我们知道,熵是系统宏观状态无序程度的定量度量.系统某个宏观状态的熵直接与这一宏观态所对应的微观状态数W有关.

式中,k为玻尔兹曼常数.

熵越大,宏观态对应的微观态越多.熵增加的过程即意味着系统从有序态向越来越无序的态转变.在这个意义上,热力学第二定律给出了孤立系统趋向于无序和混乱的时间演化箭头.

1.2 近平衡态、最小熵产生定理与远离平衡下的自组织

平衡态有两个重要的特征:a.系统的状态变量不再随时间变化;b.系统内部不存在物理量的宏观流动,如热流、粒子流等.凡是不具备以上任一条件的态,都叫非平衡态.一般来说,当系统的宏观状态不再随时间变化时,就称系统达到了定态,显然,孤立系统的定态就是平衡态.而开放系统的演化强烈地依赖于外部条件,定态有着丰富的内容和多种可能性.

热力学第二定律已经指出,孤立系统总是朝着熵增加的方向演化.熵和能量一样是可以传递的物理量,同时它还可以在自身的不可逆过程中产生出来.对于开放系统来说,熵的变化包括两部分:

式中,dSi≥0表示系统内部的熵产生;dSe为熵流,反映了系统与外界的熵交换,这部分可正、可负、也可为零.由于熵流的作用,开放系统内熵的变化可以取任何符号.

开放系统中可以存在许许多多的不可逆过程,表现为各种各样的流和力,例如,温度梯度是产生热流的不可逆力,还有由于气体分子密度不均匀而导致的扩散流等,这些流和力之间的关系,直接影响系统非平衡态的性质.

令Yi(i=1,2,…)表示各种不可逆流的强度,而把正比于温度梯度、密度梯度等的不可逆力表示为Xi(i=1,2,…),不可逆流的强度Yi依赖于不可逆力Xi的大小.当离平衡态不太远,不可逆力不大时,可以认为流与力成正比.此外,实验表明,不同的流和力之间可以相互影响,所以,当离平衡态不远时,流和力之间的关系一般应为

式中,常数Lij为线性唯象系数.

在非平衡热力学中,流和力这种线性关系适用的范围叫做非平衡线性区.

昂萨格在1932年发现线性唯象系数满足对称关系[10]

式(7)被称为昂萨格倒易关系,它直接影响着近平衡区系统演化的进程.

对于开放系统,不论是否存在与环境之间的熵流,系统内部总会由于各种不可逆过程而存在大于零的熵产生,单位时间的熵产生叫做熵产生率.由热力学第二定律可知,熵产生率不能为负.很显然,熵产生率p的大小依赖于各种不可逆过程流和力的大小,可以表示为所有不可逆过程流和力的乘积之和.

在近平衡的线性区,应用昂萨格倒易关系可以证明,系统将自发调整到使熵产生率p取得极小值的状态,这就是普利高津在昂萨格倒易关系的基础上得到的最小熵产生原理[2].

所以,孤立系统以及线性非平衡条件下的开放系统总是朝着平衡态或尽可能靠近平衡态的目标演化,即朝着无序、均匀、低级和简单的方向发展.只有当系统远离平衡态时,流和力之间不再存在线性关系,也就不会有昂萨格倒易关系和最小熵产生原理,热力学系统的演化行为才会表现出多样性,展现出各种自组织现象.

自组织现象有两个特点,一是自组织现象产生根源于系统的内部;二是系统与外界的物质和能量交换是维持有序结构的必要条件,普利高津称其为耗散结构.显然,自然界中的进化现象特别是生命现象都必须用非平衡条件下的序才能解释,所以,普利高津提出了“非平衡是有序之源”这一著名论断,远离平衡态是系统实现由无序向有序演化的必要条件.

系统状态的稳定性在耗散结构的形成过程中起着重要作用.孤立系统的平衡态和线性区的非平衡定态都是稳定状态.当某种扰动使系统偏离该状态时,系统会力求恢复到原来的平衡态或定态.通过控制外界条件,可以使系统从平衡态连续地过渡到非平衡定态,这一连串状态连接在一起,统一地被称为热力学分支.当系统离平衡态不远时,热力学分支是稳定的,而当外界条件驱动着系统越来越远离平衡时,会出现一个临界阈值,外界控制参量越过该临界值后,系统的热力学分支就失去了稳定性,微小的扰动就会使系统偏离热力学分支,并达到一个新的稳定状态,新的稳定状态所在的分支就被称为耗散结构分支,如图1所示.x0为系统稳定状态,A为外界控制参量.这种由热力学分支失稳而使系统跃迁到耗散结构分支的现象,叫做非平衡相变.

自组织现象的发生需要以下条件:a.系统是开放的.当环境造成的负熵流deS足够大而使系统的总熵减少,系统才能进入相对有序的状态.b.远离平衡态.只有当系统在外界条件驱动下达到远离平衡态的区域,才有可能发生非平衡相变.c.非线性的相互作用.这是热力学分支失稳,并存在稳定的耗散结构分支的必要条件.d.涨落是有序结构产生的触发器.在非平衡相变的临界点附近,系统中的涨落会被放大并导致系统发生宏观的变化.在非平衡系统具有了形成有序结构的客观条件后,涨落对于某种序的实现起着决定性的作用.

图1 热力学分支和耗散结构分支Fig.1 Thermodynamic branch and dissipative stricture branch

1.3 自组织现象的研究方法

以上的热力学研究给出了系统产生宏观有序行为的条件和机制,为理解各领域复杂系统的涌现性提供了统一的概念、方法和基础.但当我们希望了解具体系统的宏观行为时,必须针对具体系统应用动力学的概念和方法,分析个体行为、相互作用和演化机制.研究复杂系统的演化动力学,通常可以从宏观、介观或微观几个层次入手.

1.3.1 系统演化的宏观动力学描述

引入状态矢量x(x1,x2,…,xn)来描写系统的宏观状态,一般来说,系统的演化情况可以用反应扩散方程来描述

式中,A代表外界环境对系统的控制;D为扩散系数.

若空间均匀或不考虑空间因素且反应项中不含时间因素,该系统为n维自治微分动力系统

函数 f给出了系统演化与宏观变量x1,x2,…,xn之间相互作用的依赖关系.以(x1,x2,…, xn)为坐标轴构成了系统的相空间,相空间中的一个点代表系统的一个状态,给定初始条件,系统(10)就会给出一条相轨迹代表系统的演化.改变控制参量会改变演化过程,并定性地影响系统演化的最终结果,使系统最终稳定在不同的状态.

应用以上动力系统的描述和分析方法,利用线性稳定性分析与分支理论,就可以描述系统的非平衡相变过程.非线性系统的定态解可能有许多个,代表着系统多个不同的演化方向.因此,正像在耗散结构产生的条件中提到的,只有考虑系统中各种非线性的相互作用,才有可能描述热力学分支的失稳和耗散结构分支的形成.值得注意的是,若同时存在多个耗散结构分支,系统最终会稳定到哪个分支上,完全由在分支点附近的随机涨落决定,由此可以体会涨落是有序结构形成的触发器这一结论.当系统稳定到耗散结构的某一支上后,系统原来的时空对称性就被打破,所以,非平衡相变通常伴随着对称破缺现象.

1.3.2 自组织现象的随机描述

为了考虑系统由于微观个体偏离平均行为而导致的涨落的影响,一种途径是引入随机的描述方法,其基本观点是把系统的宏观变量或参量看作随机变量,应用Master方程、Fokker-Planck方程和 Langevin方程描写系统演化的随机过程,探讨涨落怎样触发非平衡相变和环境涨落对相变的影响等具体问题.此时人们关心的是状态变量的概率分布函数P(x,t)随时间的变化情况.

系统状态的变化需要引入转移概率,或叫迁移概率 ω来描述.对转移概率只与系统状态有关的Markov过程,分布函数随时间的演化可以用Master方程给出.时间和状态均离散的Markov链,其Master方程为

时间连续时,方程(11)化为

式中,P(j,t)为系统在t时刻处于j态的概率;ω(i→j)为系统由i态迁移到j态的转移概率.

当状态也连续时,需要使用方程(12)的积分形式.事实上,当状态和时间都连续时,可以用Fokker-Planck方程描写分布函数的演化,在1维情况下为

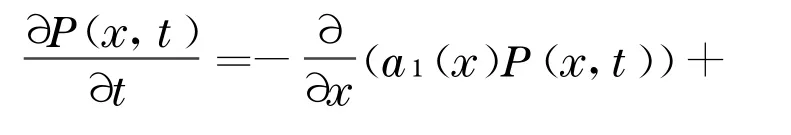
式中,a1(x),a2(x)与转移概率有关.

式中,g(x)是描述系统与环境相互作用的函数.

式(14)对应的Fokker-Planck方程为

由此可见,以上3种方程之间是有内在联系的.

自组织理论的随机方法使宏观结果与微观机制的关系有了数量上的描述,尤其可以深入讨论涨落是如何被放大的、环境涨落对自组织过程的影响等问题,加深了人们对系统演化的理解.

1.3.3 自底向上的多主体模拟方法

反应扩散方程中的反应项和主方程中的转移概率,实质上都是对系统微观层次相互作用的描述.对于由具有主动性、适应性的个体组成的复杂系统,系统个体之间相互作用和宏观状态演化的结构化描述非常困难.此时以多主体模拟方法为代表的自底向上的复杂系统研究方法,就成为理解和研究自组织现象的基本手段.

元胞自动机可以认为是最简单的多个体模拟方法.元胞自动机实际上是空间、时间、状态都离散的动力系统,元胞之间的相互作用通常是通过if-then之类的逻辑语言描述,通过计算机数值模拟研究系统最终的演化结果,探讨在各种条件下有序结构的形成.在大量社会、经济、生物、生态系统中,个体的行为和相互作用更加复杂,甚至具备学习能力和适应行为,复杂适应性系统的概念和研究方法就是在这种情况下发展起来的[11-13].

使用多主体系统模拟方法研究复杂系统中自组织行为,人们最关心的是个体仅仅通过局域范围内的相互作用,在一定条件下就会产生全局性的时空结构或组织结构.自底向上的计算机数值模拟方法,需要确定个体和环境特征、个体之间的相互作用机制、演化机制、宏观结构的刻画等要素,自组织现象的产生条件、机制和特征在相关模型机制设定中都会有所体现.在多个体系统模拟中,人们更应该关注自组织现象的本质内涵:在没有中心控制(没有组织者或其他系统之外的设计)、没有完全信息的条件下,仅仅通过微观个体的局域相互作用,就可以导致系统全局结构的涌现[14].

2 生命系统中的应用案例

现以心肌组织中螺旋波的演化行为为例,沿着从微观到宏观这一线路,应用自组织理论加深对相关问题的理解.

螺旋波是一种典型的宏观时空有序结构,在自然界中尤其是生命系统中十分常见,如铂表面的CO氧化反应、液晶中的Ising-Block相变、粘性霉菌群体的自组织演化、卵细胞中的钙离子波等.在心肌组织中,心肌细胞间传导的电信号也可能在宏观上产生螺旋波.螺旋波的一个显著特点就是能够自我维持,一旦产生就很难自然消除.而且螺旋波极易受到噪声或是外界环境的影响发生破裂,进入到湍流态或混沌态,使得心肌组织的有序行为受到破坏,出现心颤.因此,对心肌中螺旋波产生、演化、破裂行为的研究有现实意义.

首先从微观入手.假定组成心肌组织的所有心肌细胞都是同质的,不妨先考虑单个细胞的行为和性质,这是出现宏观电信号的微观基础.基于实验中观察到的细胞膜电位发放过程,日本电机工程学家Nagumo于 1962年对完全描述细胞膜机构的Hodgkin-Huxley模型进行简化,提出了 FHN (FitzHugh-Nagumo)模型[15]

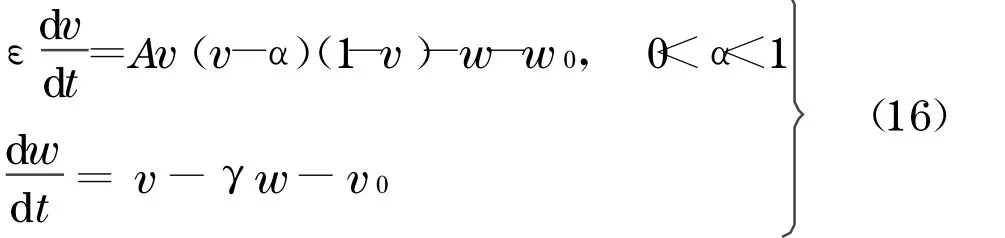
式中,系统变量v为膜电压;w是与动作电位后恢复期大小有关的变量;v0,w0为两个变量的参考值;α, γ为系统参数;ε为一远小于1的参数,表示两个变量v,w具有不同的时间尺度,分别为系统的快变量和慢变量.

将两个动力学项简记为

由动力系统的定性分析方法容易得到,系统(16)存在唯一的不动点,通过线性稳定性分析可知,当ε是一个小量时,这个点是渐进稳定的.也就是说,系统状态一旦进入该点的邻域内时,就会最终到达并稳定在这个不动点,即使受到一个小的扰动,系统也会最终回到这个状态.但同时ε使变量w的变化速率远小于变量v的变化速率,当扰动超过一定阈值时,系统就表现出特殊的动力学行为.如图2(a)中实线所示,系统首先会被很快地激发到远离定态解的区域,然后按照某个路线弛豫回到系统定态.虚线为FHN方程的水平等倾线和竖直等倾线,实线代表系统受激发后的相轨线.这种系统称之为可激发系统,其中,动力学项的三次函数形式是系统可激发的一个必要条件,而ε值的大小是系统可激发性的一个重要量度,只有在ε值足够小时,系统才是可激发的;否则,系统的稳定点将是一个稳定焦点,不会观察到激发过程.

图2 FHN方程的相图和时间演化图Fig.2 Phase diagram and time evolution of FHN equation

定性了解了单个细胞的可激发性质之后,可以进而研究心肌组织上整体显现出的宏观动力学行为.此时就必须考虑细胞之间的耦合以及电信号在细胞之间的扩散传播,需要用带有空间扩散项的反应扩散系统来描述系统的整体行为

式中,D为扩散系数,扩散项表示细胞状态值受其他细胞的影响.

对反应扩散方程(17),理论分析通常十分困难,计算机数值计算方法就成为一个非常必要的工具.

通过数值模拟结果可以很直观地看到,在特定系统参数范围内,断裂的行波由于细胞之间扩散的相互关系,会内卷形成螺旋波,而之后的动力学行为,由系统参数(与微观个体及其相互作用关系相关)和外界环境共同决定.稳定的螺旋波,其波尖的运动轨迹是一个稳定的圆,随着系统参数的变化,螺旋波会出现多次相变和失稳,开始漫游直至破裂[16].而改变外界环境,如外加力场等,也可以控制螺旋波出现漂移等行为.之前的工作就同时考虑了这两个因素的影响,在均匀介质的条件下由系统参数的不同可以得到疏密两种螺旋波,如图3所示,当介质变得不均匀时,这两种螺旋波的漂移行为有很明显的差异[17].从微观的可激发的细胞到宏观组织中的时空有序结构,很好地体现了自组织现象的产生过程和研究方法.

图3 螺旋波示意图Fig.3 Spiral wave

3 自组织理论的拓展和应用

自组织理论的建立,直接推动了复杂性研究的发展[18-19].进入21世纪以来,复杂性研究得到了各国科学研究工作者的重视,使得自组织理论迅速发展,无论是概念体系、理论范畴或研究领域都得到了拓展.

从动力学的研究层面上,随着非线性科学的发展,经典意义上的以时空周期结构或准周期结构为特征的自组织概念已被大大地加以扩展,关于混沌、分形及孤子理论的相继问世,使大家开始关注以混沌组织形态为代表的更复杂、更一般的自组织形态.同时,随着经典动力系统与对应的量子系统特征对照研究手法的发展,探讨经典动力系统行为的混沌化的量子对应得到迅速发展,对量子混沌现象的深入研究使得源于宏观层次上的自组织理论研究深入到了微观层次.

自组织理论问世之初研究的对象主要集中在反应-扩散系统及激光等物理化学系统,但随着对自组织认识的深化及研究层次的拓展,特别是探索复杂性命题的提出,研究对象的类型也在过去30年中逐步扩展和多样化,从物理和化学系统中的自组织研究向地质学、气象学、宇宙学,特别是向生物学及社会系统中的自组织研究拓展.地质学中的成矿及其分布、气候的演变、地震活动的演化、生物体内的节律现象与自调节功能、细胞动态特征中的自组织行为,以及交通控制、城市发展和人口控制中的自组织模型等研究皆取得显著成功,为深入研究各领域有序结构的形成机制,能动地利用自组织理论达到控制各类系统的演化,使其实现特定的结构和功能打下了基础.

4 结束语

自组织理论的研究对象是复杂系统,它关心复杂系统演化所表现出来的多样性和复杂性背后的基本科学问题.自组织理论的产生和发展,成为沟通物理的、量的世界和生物的、质的世界的桥梁.这一理论对于人们的世界观和方法论产生了革命性的、深远的影响,使人们认识到了不同领域内的复杂系统,在演化过程中遵从着普适的规律,而要挖掘这些基本的规律,在科学方法上就必须超越还原论,使用整体论和系统论的研究方法.这些思想和方法上的革新奠定了探索复杂性的科学基础.

探索复杂性目前已经成为科学研究的一个热点领域,引起了世界各国科研工作者的重视.我国2006年发布的《国家中长期科学和技术发展规划纲要》也多次论述了系统科学和交叉学科,明确指出“复杂系统、灾变形成及其预测控制”是面向国家重大战略需求的基础研究,要求“重点研究工程、自然和社会经济复杂系统中微观机理与宏观现象之间的关系,复杂系统中结构形成的机理和演变规律、结构与系统行为的关系,复杂系统运动规律,系统突变及其调控等,研究复杂系统不同尺度行为间的相关性,发展复杂系统的理论与方法等.”作为自组织理论的进一步发展,我们相信这一研究方向最终会加深我们对自然和生命的理解.

[1] GLANSDORFF P,PRIGOGINE I.Thermodynamics Theory of Structure,Stabilityand Fluctuations[M]. New York:Wiley-Interscience,1971.

[2] 尼科利斯,普利高津.非平衡系统的自组织[M].徐锡申,陈式刚,王光瑞,译.北京:科学出版社,1986.

[3] PRIGOGINE I.From Being to Becoming[M].San Francisco:W H Freeman and Company,1980.

[4] 沈小峰,胡岗,姜璐.耗散结构论[M].上海:上海人民出版社,1987.

[5] 哈肯 H.协同学引论[M].徐锡申,陈式刚,陈雅深,译.北京:原子能出版社,1984.

[6] 哈肯H.高等协同学[M].郭治安,译.北京:科学出版社,1986.

[7] HAKEN H.信息与自组织[M].成都:四川教育出版社,1988.

[8] 湛垦华,沈小峰.普利高津与耗散结构理论[M].西安:陕西科学技术出版社,1982.

[9] 姜璐.自组织理论——复杂性研究的欧洲学派[M]//复杂性新探.北京:人民出版社,2007:123-135.

[10] ONSAGER L.Reciprocalrelationsin irreversible processes[J].I Phys Rev,1931,37:405-426.

[11] 约翰◦霍兰.隐秩序:适应性造就复杂性[M].周晓牧,韩晖,译.上海:上海科技教育出版社,2000.

[12] HOLLAND J.The Echo Model[C]//Proposal for a Research Program in Adaptive Computation,1992: 15-30.

[13] HOLLAND J.Adaptation in Natural and Artificial Systems[M].2nd ed.Cambridge,M A:MIT Press,1992.

[14] 姜璐,张方风.要加强对复杂适应性系统的研究[J],系统科学学报,2008,16(1):25-30.

[15] NAGUMO J,ARIMOTO S,YOSHIZAWA S.An active pulse transmission linesimulating nerve axon[J]. Proc IRE,1962,50.

[16] WINFREE A T.Varieties of spiral wave behavior:An experimentalist's approach to the theory of excitable media[J].Chaos,1991,1(3):303-334.

[17] XU L,QU Z,DI Z.Drifting dynamics of dense and sparse spiral waves inheterogeneous excitable media [J].Phys Rev E,2009,79:036212,1-5.

[18] PRIGOGINE I,ALAN P M.The Challenge of Complexity,Self-Organizationand Dissipative Structures [M].Austin:University of Texas Press,1982.

[19] NICOLIS G,PRIGOGINE I.探索复杂性[M].罗久里,陈奎宁,译.成都:四川教育出版社,1992.