海底电力电缆铠装结构机械强度分析及设计

夏 峰， 陈 凯， 张永明

(宁波海缆研究院，浙江宁波315040)

0 引言

随着我国海洋经济的快速发展，高电压等级海底电力电缆(以下简称海缆)得到了广泛应用。由于海缆的外径不断增大，要求海缆本身具有更高的机械强度，以便承受重力荷载;同时海缆在敷设以及运行中，尤其是海缆发生故障需要打捞修理时，将承受比正常敷设时更大的荷载，这些都对其机械强度提出了更高的要求。由于海缆的功能单元结构相对固定，而且原则上不作为承载单元，提高海缆机械强度一般采用的方法是在海缆功能单元外增加一层或者多层钢丝铠装，因此铠装的设计就成为海缆机械强度设计的关键。

1 海缆铠装预设计

由于钢丝铠装为螺旋绞合的复杂结构，其机械强度的计算非常困难。在对海缆进行机械强度设计前，须对设计过程中所用的理论作基本假定，以明确其需要满足的必要条件。

1.1 海缆铠装设计的基本假定［1］

(1)同一截面上的所有铠装钢丝有相同的伸长和扭转等变形量，即平截面假定;

(2)海缆在初始无受力状态时层间没有摩擦;

(3)铠装钢丝所发生的力学行为皆在弹性范围内;

(4)忽略层间和层内的摩擦，忽略层间的互相作用力，层间可完全滑动。

1.2 每层铠装覆盖的密集度

根据铠装覆盖密集程度的不同，相同的海缆节圆半径可以有不同的铠装钢丝根数。通常选取的铠装覆盖密集度在90% ～100%，因为在这个范围内铠装结构具有更好的稳定性。根据几何关系，可以得到一个近似计算铠装覆盖密集度Ci的方法，其误差在设计允许的范围内［2］:

式中，Ci为铠装覆盖密集度(%);ni为每层铠装钢丝根数;Ri为铠装层的节圆半径(mm);αi为缠绕角度(°)。必须说明的是，力学设计中的铠装角度与电缆行业所定义的铠装螺旋升角互为余角;同时，在确定铠装覆盖密集度的条件下，也可以根据铠装层的节圆半径和缠绕角度得到每层铠装钢丝的根数。

1.3 扭转平衡与应力平衡

如上所述，为使铠装结构有较大的轴向刚度，同时又有较好的弯曲柔度，通常将其设计成为螺旋缠绕形式。这种结构会使得铠装在受到拉伸载荷时产生一个使铠装螺旋松开方向的扭矩，即与铠装层绞合方向相反的扭矩。在一端固定另一端可以自由转动的情况下，这个扭矩会造成不同层铠装松紧不一。这就意味着在受拉的情况下，紧的铠装层将承受比松的铠装层更大的应力，造成应力分布不均，显著降低了海缆的抗拉能力。同时在海缆两端的扭转自由度都能被限制的情况下，如果没有足够的拉力，这个扭矩还会使海缆产生局部弯扭和打结等失稳变形。为了减小因铠装螺旋缠绕所产生的扭矩以及避免存在的失稳风险，通常将多层铠装设计成相邻层互为相反的缠绕方向。

为了提高结构的承载效率，我们希望每层铠装都承受与之屈服强度成比例的载荷。这就是应力的平衡。

Knapp等学者已经证明［3］，只要满足公式(2)，海缆的扭转以及应力平衡就可以近似地得到满足:

式中，L 为总层数;i、d 为层数序号(1，2，3，…，L);A为铠装横截面积(mm2);Sy为铠装屈服强度(MPa)。

2 海缆的铠装强度设计

海缆的机械强度在很大程度上取决于其刚度的大小。因为刚度大的海缆在相同变形量的情况下，能承受更大的荷载，即具有更大的机械强度。由于海缆的功能单元结构相对固定，因此，其主要通过铠装单元的设计来优化海缆的刚度。在相同的铠装层节圆半径下，铠装刚度将会随着缠绕角度、单根钢丝直径以及铠装截面形状的变化而改变。这其中主要的设计参数为缠绕角度和单根铠装钢丝的直径。

2.1 铠装缠绕角度的设计

较小缠绕角度的铠装结构具有较大的抗拉刚度，但同时弯曲的柔度也较低;当铠装缠绕角度变大时，其导致结果正好反之。因此，只有通过合理选择铠装的结构设计参数，才能找到最优的平衡点，以满足海缆对强度和刚度的要求。

2.1.1 缠绕角度与拉伸刚度的关系

对于两端固定的线缆而言，拉伸刚度为 kTε(MN)，计算公式如下［4］:

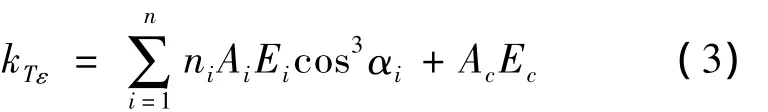
式中，i为铠装层层数;c为内核组份;E为弹性模量(MPa);AcEc为内核组份的整体抗拉刚度(MN)。

同时铠装的根数与缠绕角的关系可表示为:

图1为铠装拉伸刚度与缠绕角的关系(注:拉伸刚度比值为“无量纲”，设缠绕角度为0°时的拉伸刚度为1.0)。

图1 铠装拉伸刚度与缠绕角度的关系

从图1可知，当缠绕角度从0°增加到10°时铠装的拉伸刚度减小并不明显，10°时的拉伸刚度约为0°时的0.94 倍;当缠绕角度从 10°增大到 20°时，铠装的拉伸刚度衰减率开始变大，20°时的拉伸度约为0°时的0.8倍;当缠绕角度大于20°时，铠装拉伸刚度的衰减速率进一步加大，30°时的拉伸刚度约为0°时的0.56倍，铠装的抗拉性能明显削弱。由于在海缆设计中铠装所提供的拉伸刚度能达到整缆的60% ～80%。因此，为使整缆有较大的拉伸刚度，通常建议铠装缠绕角度不大于20°(注:即螺旋升角不小于 70°)。

2.1.2 缠绕角度与弯曲刚度的关系

按照full-slip模型，此时海缆的弯曲刚度可表示为［3］:

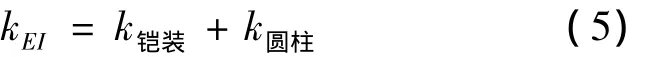
式中，KEI，K铠装，K圆柱分别为海缆、铠装层和圆柱体(内核)的弯曲刚度(kN·m2);EI为铠装钢丝截面的抗弯刚度(kN·m2);GJ为铠装钢丝截面的抗扭刚度(kN·m2);i为圆柱体层数;D为圆柱体外径(mm)。

根据公式(6)可得到铠装弯曲刚度与缠绕角度的关系图(见图2)。图中弯曲刚度比值与拉伸刚度比值一样为无量纲，设缠绕角度为0°时的弯曲刚度为 1.0。

图2 铠装弯曲刚度与缠绕角度的关系

与铠装的拉伸刚度相似，弯曲刚度随着铠装的缠绕角度增大而减小，但与拉伸刚度要求不同的是希望海缆具有较小的弯曲刚度，因为在海缆的生产、运输以及安装过程中常常需要经受反复的弯曲。增大缠绕角度能减小弯曲刚度，这同时会减小拉伸刚度，所以一般不宜采用过大的缠绕角。

2.2 铠装钢丝的直径设计

2.2.1 弯曲刚度与铠装钢丝直径的关系

图3为铠装钢丝直径与弯曲刚度之间的关系(注:弯曲刚度比值为无量纲，设直径为1mm钢丝时的弯曲刚度为1.0)。从图3中可以发现，选用较小的铠装直径能大大提高铠装的柔性从而提高整根海缆的弯曲性能。

图3 弯曲刚度与铠装钢丝直径的关系

2.2.2 拉伸刚度与铠装钢丝直径的关系

图4反映了铠装直径与拉伸刚度之间的关系(注:拉伸刚度比值为无量纲，设直径为1mm钢丝时的拉伸刚度为1.0)。从图4中可知，拉伸刚度随着铠装直径的增大而提高，且近似为线性关系。

图4 拉伸刚度与铠装钢丝直径的关系

2.2.3 铠装钢丝直径与扭转刚度的关系

图5为铠装钢丝直径与扭转刚度的关系(注:扭转刚度比值为无量纲，设直径为1mm时的扭转刚度为1.0)。从图5可知，铠装的扭转刚度随着铠装钢丝直径的增大而提高，且近似于线性关系。

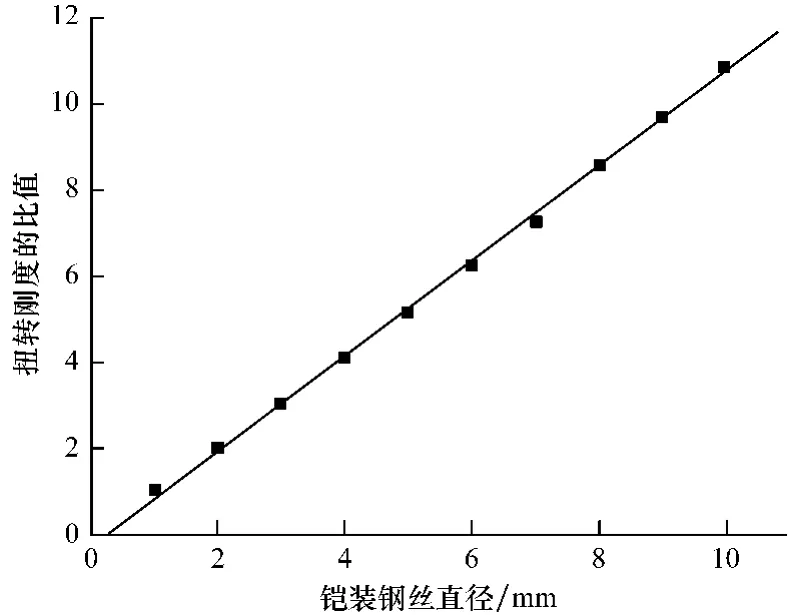
图5 扭转刚度与铠装钢丝直径的关系

3 理论计算方法的验证

由于铠装理论计算的基本假设在现实情况中不能严格满足，为验证计算方法的可靠性，需要通过数值方法和试验对理论计算的结果进行验证。数值计算方法有限元计算在国外已经成为一个有效的海缆设计手段。由于本文篇幅所限，以及基于有限计算的复杂性，对此不作详细论述。

根据文献［4］报道，国外某公司通过专用机械强度测试装置进行验证实验(见图6)，结果显示理论计算值略大于有限元数值计算和试验值，尽管理论计算有一定误差，但可以满足工程设计的要求，产生误差的主要原因如下:

(1)理论计算忽略了摩擦对铠装刚度的影响;

(2)理论计算忽略了层间的互相作用;

(3)理论计算采用线性模型，忽略了材料、几何非线性等。

从图6可知，理论计算要大于数值计算以及实验值，存在一定误差［5］。

图6 理论计算数值分析以及试验结果的对比

4 结束语

正如上述，铠装机械强度理论计算模型为海缆的铠装设计提供了一个较为简洁而又相对可靠的设计方法，同时由于海缆复杂的几何条件和边界条件，使其在计算中会引起一定的误差。有限元方法能较好地弥补理论计算的不足，并能对理论计算结果的准确性进行验证。有限元建模的方法有很多，可以选用实体建模，以及梁单元结合壳单元建模，在这里不做一一论述。最后，还要通过实验对理论及有限元数值计算方法及其结果进行验证，并对计算模型进行修正，这样才能最终保证结果的可靠性。

［1］Custo dio A B，Vaz M A.A nonlinear formulation for the axisymmetric response of umbilical cables and flexible pipes［J］.Applied Ocean Research，2002(24):21-29.

［2］Nowak，G.Computer design of electromechanical cables for ocean applications［C］//Proc.10th Annual MTS Conf.，Washington，D.C.，1974.293-305.

［3］Knapp R H.Torque balance design for helically armored cables［J］.ASME J.of engineering for industry，1981(83):61-66.

［4］Ian Probyn(DUCO)，Alan dobson(DUCO)and michal martinez(IFP).Advances in 3-D FEA techniques for metallic tube umbilicals，proceedings of the sixteenth(2007)international offshore and polar engineering conference lisbon［C］.Portugal，July，2007，1-6.

［5］Svein Savik，Knut I，Ekeberg.Non-linear stress analysis of complex umbilical cross-sections.OMAE［C］.2002.28126.