电磁场对屏蔽电缆耦合的研究现状及发展趋势

王川川，朱长青

(军械工程学院电气工程系，河北石家庄050003)

军用移动电站给军用装备供电的长电缆极易耦合电磁信号，成为空间电磁信号的接收天线，给用电装备和发电系统造成干扰甚至破坏。对屏蔽不够好的电站和武器装备来说，长电缆通常会成为引进干扰的主要途径。

为了提高电站的电磁防护能力，首先就要研究电线电缆的电磁防护，使得电线电缆上产生的电磁干扰信号降至最低限度。本文对国内外在电线电缆对空间电磁场的耦合及防护方面的研究进展进行了

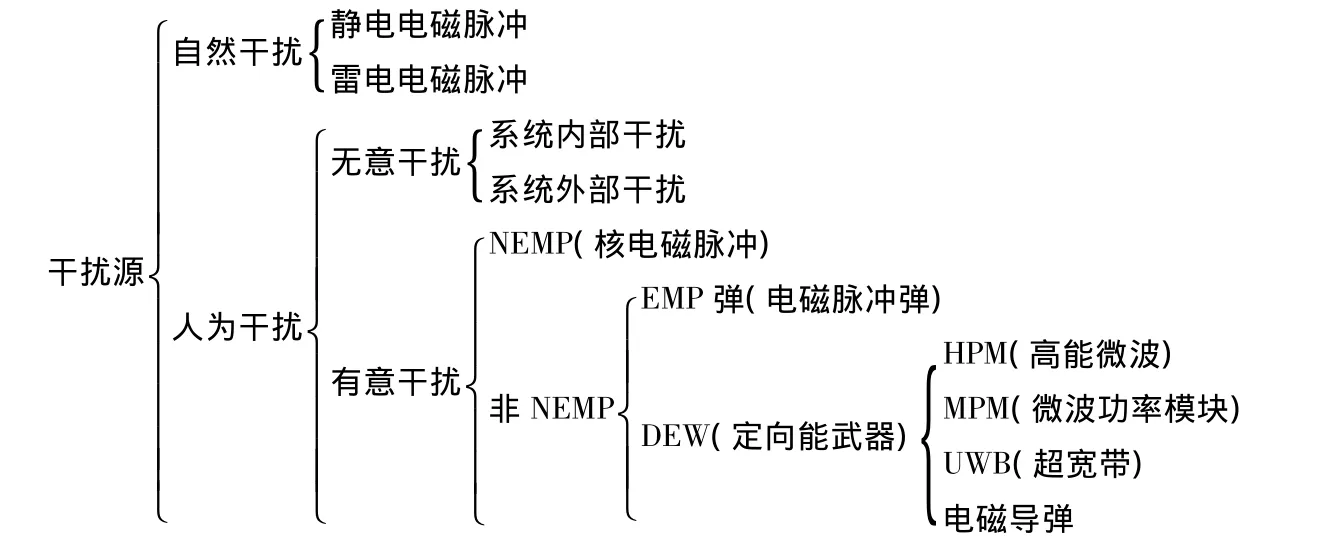
图1电磁干扰源构成

电磁干扰源产生的电磁干扰依据一定的耦合途径到达敏感设备，从而对敏感设备的工作产生影响。研究表明，电磁干扰作用于敏感设备必须具备三个条件:干扰源、能量传输途径和敏感设备。图2为电总结，归纳了常用的研究方法以及常用防护措施，介绍了电线电缆电磁防护问题的研究发展趋势。

1 电线电缆在电磁防护方面的研究内容

(1)电磁干扰源及干扰途径［1］。电磁干扰源既有自然干扰源，又有人为干扰源。具体到战场环境中，起主要作用的是各种人为的电磁干扰源。现代战场的电磁干扰源构成如图1所示。线电缆遭受电磁干扰的示意图。

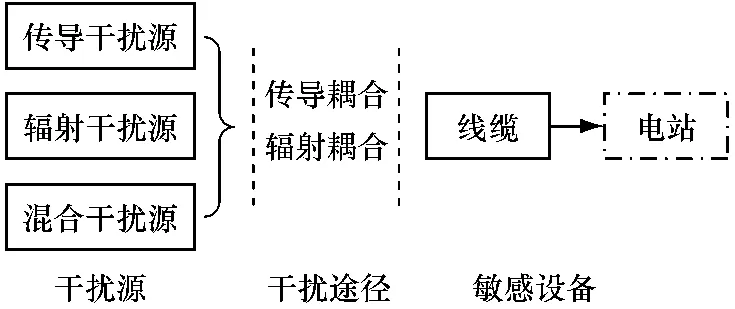
图2 电线电缆遭受电磁干扰示意图

(2)线缆屏蔽结构的研究，包括各类屏蔽材料、形式或组合结构，大致包括:①金属管状结构;②金属丝编织(不同编织密度)结构;③金属丝缠绕(不同密度)结构;④金属薄膜重叠绕包(或纵包)结构;⑤钢带铠装结构;⑥金属镀层(包括物理或化学镀层)结构;⑦半导电屏蔽材料的屏蔽作用;⑧导电漆膜结构;⑨以上组合结构。

(3)线缆不同传输形式的研究，包括:①对绞;②对绞屏蔽;③星绞;④星绞屏蔽;⑤同轴结构;⑥双同轴对称射频结构(分屏蔽后加总屏蔽);⑦三同轴结构;⑧漏泄电缆的耦合(利用电磁耦合)。

(4)不同屏蔽结构、不同传输形式的线缆在不同频段或不同场源情况下耦合干扰信号机理及防护措施的研究。

(5)不同屏蔽结构、不同传输形式的线缆的转移阻抗与转移导纳的计算、测量方法研究。

(6)线与线之间的串扰与互耦。

2 场线耦合问题国内外研究概况

2.1 国外研究概况

国外早在20世纪60年代就开始了线缆耦合电磁场的研究，下面对其研究中所采用的理论和取得的主要成果进行介绍。

Vance.E.F［2］运用传输线模型来研究空间电磁场与架空输电线路、空间电磁场与地下屏蔽电缆的耦合，给出了管状屏蔽和编织型屏蔽两种同轴电缆的转移阻抗和转移导纳的计算及测量方法，没有研究多导体、多层屏蔽的电缆对空间电磁场的耦合，也没有解决这种电缆的转移阻抗和转移导纳的计算及测量方法。Michel Aguet、Mircea Ianovici和 Lin Chung-chi［3］将空间电磁场与屏蔽电缆之间的复杂耦合问题分解为两个相对简单的关联的内、外传输线系统，外传输线系统由屏蔽电缆的屏蔽层和大地构成，由此系统计算得到在空间电磁场激励下的屏蔽层电压和电流响应，内传输线系统由屏蔽电缆的屏蔽层和芯线构成，由此系统计算得到芯线上的响应，两个传输线系统由转移阻抗及转移导纳联系在一起。D’Amore.M，Feliziani.M 和 Celozzi.S［4-6］根据场线耦合的内外传输线模型，研究了空间电磁场与同轴屏蔽电缆、空间电磁场与屏蔽多导体平行芯线电缆及螺旋状芯线电缆的耦合和空间电磁场与无屏蔽多导体平行芯线电缆及螺旋状芯线电缆的耦合等，通过运用电路模型理论最后推导出空间电磁场与屏蔽电缆响应之间的集中参数矩阵方程关系。Arlon T.Adams、Jose Perini等［7］研究了超高频及以上频率电磁场对线缆的耦合，在这种情况下，电缆将变为电大尺寸，线上感应电流的分布为驻波或行波模式，电流将出现反射。Tesche.P.M 等［8］研究了空间电磁场与架空输电线路之间的耦合，给出了空间电磁场激励下计算架空线响应的格林函数，由此函数可以很方便地计算架空输电线路上任意点处的响应，没有研究空间电磁场与屏蔽多导体电缆的耦合。另外，Belifuss.J［9］运用模式传播理论求解空间电磁场激励下的多导体传输线响应，建立了传输线响应的最大值与传播模式之间的关系，但是此种方法非常烦琐。

对于屏蔽电缆的转移阻抗与转移导纳的计算与测量，许多学者作出了不懈的努力，提出了一些模型与方法。基本做法是在电缆屏蔽层加上一个已知的电压和电流信号，然后测量电缆芯线上感应到的电压和电流信号，最后根据一定的计算方法得到转移阻抗和转移导纳。这些方法能应用于GHz以下环境，但存在适用的电缆种类有限，计算方法、测量装置复杂、代价较高等问题。Kley.T［10］提出了一种测量方法，使屏蔽电缆转移阻抗和转移导纳的测量大大简化，测量装置简单，花费较少，但该方法应用范围有限，只适用于单芯屏蔽电缆。为了得到屏蔽电缆的转移阻抗和转移导纳，Helmers.S和 Gonschorek.K.H［11］提出将矩量法(MOM)传输线理论(TLT)和实验测量法相结合，可得到一种快速、简便的方法。他们还研究了在什么情况下转移阻抗和转移导纳在场线耦合中各自起到主要作用。Orlandi.A［12］利用SPICE软件，建立了屏蔽同轴电缆转移阻抗和转移导纳的计算模型，该模型应用范围比较有限。

有文献指出，对于线缆之间的互耦，受扰线上感应电压比干扰线上电压低很多，但却处于同一数量级。Levin.B.M［13］研究了两芯通信电缆转移阻抗和转移导纳的计算方法，在研究中发现芯线之间的耦合是通信电缆电磁干扰的重要来源，这说明线缆之间的互耦有时能产生很大的影响，是不可忽视的干扰源。

综合国外研究文献来看，国外对场线耦合问题的研究基本理论都来自E.F.Vance的研究成果。随着其他技术的发展及其在场线耦合分析中的应用，又出现了一些新的计算模型，如文献［14］等。对于复杂环境中的屏蔽电缆，在计算电缆屏蔽层上的感应信号时，也可以采用一些现有的软件计算电缆屏蔽层上的响应，如FEDELITY软件、FEKO软件等。在计算电缆芯线响应时，一般仍采用传输线模型进行求解。

在场线耦合问题的研究中，国外学者做了很多实际的、有开创性的工作，提出了一些经典、常用不衰的计算模型和方法，发展了一些实用的算法。由于该问题的复杂性，并且很多方面仍是未知领域，或未完全搞清，主要包括以下方面:

(1)前人的研究中有很多屏蔽结构、传输形式的线缆耦合电磁场的机理没有涉及到;

(2)前人的研究中，很多研究方法是经过将研究对象简化的结果，与实际情况偏差较大;

(3)现有的屏蔽电缆的转移阻抗、转移导纳计算和测量方法存在适用范围有限、技术复杂、代价高昂等问题;

(4)在研究一些新的电磁干扰源对线缆的耦合时，采用经典的模型和方法已不能得到十分满意的结果。

2.2 国内研究概况

国内对于屏蔽电缆耦合电磁场问题的研究高潮起于20世纪90年代末。大多数研究基于传输线理论［15-23］，少部分采用了时域多分辨分析方法［24］，也有一些混合算法获得了应用［25］。随着计算机技术的高速发展，采用全波分析法，将电缆耦合问题作为电磁散射问题来分析已成为可能。目前国内采用场的时域有限差分法(FDTD)仿真计算了空间电磁脉冲对电缆屏蔽层的感应电流［26-31］，较少进行电缆芯线电流的计算。屏蔽电缆的转移阻抗和转移导纳仍是研究的一个热点。在多导体屏蔽电缆对电磁脉冲耦合的研究中，主要集中在多导体电缆参数的提取上［32，33］，对于多导体之间串扰的研究较少。在实验测量方面，测量的重心多在研究电缆屏蔽层的电流，及分析影响电缆屏蔽层电流的相关参数［34］，对电缆芯线感应信号的测量非常少。

3 常用的研究方法

研究电磁场对传输线的耦合问题的分析方法大体来说可以分为两类，即场的方法和等效路的方法。

3.1 场的方法

这种分析方法直接从Maxwell方程组出发，对各场分量进行严格求解，理论上较为严格。随着计算电磁学的不断发展，对电磁场问题作时域全波分析成为可能，逐渐发展了一些新的时域全波分析算法。其中比较典型的计算方法有:

(1)时域有限差分法。FDTD法在分析线缆耦合方面已有较长应用历史，它可以采用全波分析法，将电缆耦合问题作为电磁散射问题来分析。FDTD法是分析电线电缆耦合电磁场问题的有力手段，然而，在实际应用时它仅适用于相互平行的导体结构，对于垂直导线结构以及其他复杂导体则不能处理。该算法还存在对计算机内存要求较高和计算时间较长的问题。目前的主要发展方向是提高计算精度，增加模拟复杂媒质和结构的能力(特别是对不同媒质分界面处的模拟)，减少对计算机存储空间等硬件水平的需求等。近年来，有多种FDTD法的变形出现，文献［35］举出了较具特色的几种。

(2)传输线矩阵方法。传输线矩阵法建立在传输线理论上，也被用来分析传输线上任一点的电压与电流的分布情况。传输线矩阵法TLM是和FDTD法几乎同时发展起来的时域方法，但其应用不如后者广泛，原因在于与FDTD法相比，这种方法的运用较为复杂，需要进行电路参数和场量之间的转换，而且占用计算机内存较大，计算效率相对较低。此外，该方法对非均匀网格的处理能力和吸收边界的作用效果尚待提高。随着研究人员的努力，TLM方法也在不断发展［36-38］。

(3)时域积分方程法(TDIE)。该法近年来发展迅速，但是因一些因素的制约而限制了它的实际应用，例如存在后期不稳定的问题。目前改善TDIE后期不稳定性的方法有:平均法、时域混合场积分法、隐式法、滤波器法、新型的时间基函数法、精确计算时域积分方程的阻抗矩阵元素等。

此外还有许多其他的算法，如时域有限元法(FETD)、多分辨率时域技术(MRTD)、时域伪谱算法(PSTD)等。文献还提到出现了不同算法的结合，以及信号处理技术与算法的结合。

3.2 路的方法

这种方法通过所分析的电缆系统建立起一组等效的传输线方程，在一定的近似条件下，将电缆内外电场和磁场的耦合简化成电缆内外电流、电压通过屏蔽电缆的转移阻抗和转移导纳的耦合关系，从而求解电缆外部空间电磁场激励时引起的内部响应，这类方法比较简单实用。

Helmers.S.和 Gonschorek.K.H 研究发现，传输线模型有一些局限性［39］，针对这些问题，F.M.Te-sche等指出如果电缆和大地组成系统满足两个条件:一是大地为完纯导体，电缆和它在大地中的镜象导体成完全对称状态，此时共模电流非常小，只需考虑差模电流;二是在感兴趣的频率范围内，传输线的横向尺寸为电小尺寸，即与波长相比很小，即可运用传输线理论进行分析［40］。

由于传输线模型简单，易于考虑电缆参数的频变特性，且能满足工程实践的需要，因此在场线耦合机理研究中得到了广泛的应用。学者们提出了场线耦合计算模型，主要有 Taylor模型、Agrawal模型、Racchidi模型等。至于 Vance.E.F的模型，基本与Agrawal模型相同，但有所简化。由于Agrawal模型中只用到了沿线电场分量作为激励，因此模型简单，但在终端边界条件处理方面比Taylor模型复杂。由于实际应用中传输线多为耦合多导体传输线，因此实际应用中的场线耦合问题可以归结于耦合多导体传输线的场线耦合问题。以上述三种传输线模型为基础，国内外学者对耦合多导体传输线耦合响应进行了大量的研究，大多数研究均在准TEM波近似下，用一组频域常微分方程或时域偏微分方程来描述传输线的分布参数电路模型，进而在给定的初始条件及边界条件下求解这些方程。研究中所采用的方法可以分为两类:

(1)频域分析方法。该方法可以处理频变参数。但由于在处理瞬态问题时，必须采用傅立叶变换，当瞬态电磁过程上升时间很短时，计算工作量较大，有可能引起失真和混叠等问题。此外，频域分析方法只能处理线性问题，不能处理非线性问题和非均匀传输线，也难于处理非零初始条件问题。目前，采用其他数值变换的方法逐渐应用于该方法中。

(2)时域分析方法［41］。包括贝杰龙(Bergeron)法、等效集总参数电路模型法、特征法、网格法以及FDTD等方法，这些算法工作量较少，且结果直观，可以处理非线性系统，但不易处理频变参数问题。

对于瞬态电磁场的计算，首选的方法当然应该是时域分析方法。但是由于场的方法计算量太大，计算的时间也很长，且对于电磁脉冲对传输线的耦合问题，按传输线理论的方法作近似分析，计算出的结果在工程上精度是足够的，因此采用等效路的方法中的时域算法是很好的选择。这其中等效路的FDTD法秉承场的FDTD法的优点，不仅可以计算出传输线上任意点的电压、电流波形，对于非均匀传输线的求解也比较方便，因此越来越受到关注。

4 结束语

屏蔽电缆是空间电磁能量的巨大收集器，对电缆耦合空间电磁场问题的研究具有重要的理论意义和实用价值。近年来国内外许多学者进行了大量的研究，并取得了很大进展，提出了一些防护技术，产生了实际的价值。但总的说来，电缆对空间电磁场的耦合及其防护技术还研究得不够，还不能完全做到对电缆的有效防护，一些关键技术还亟待解决。本文认为在以下几方面值得深入研究和探索:

(1)目前的研究主要集中在平行直导体传输线和电缆上，对任意弯曲传输线和电缆的研究较少，线缆弯曲对传输高频信号的影响仍不甚清楚，要加强这方面的研究;

(2)努力寻找不同类型电缆的转移阻抗和转移导纳的计算和测试方法;

(3)发展更加实用的算法，改进现有算法，在算法的推广应用方面，为克服愈发复杂的算法理论给使用者带来的困难，要努力发展相应算法的仿真软件;

(4)在解决复杂研究对象的建模问题方面，要继续研究和发展自适应、智能化的建模技术;

(5)多导体屏蔽电缆耦合空间电磁场，以及不同导体之间的串扰的研究有待加强。

［1］孙国至，刘尚合，陈京平，等.战场电磁环境效应对信息化战争的影响［J］.军事运筹与系统工程，2006，20(3):43-47.

［2］爱·弗·万斯著，高攸纲，吕英华译.电磁场对屏蔽电缆的影响［M］.北京:人民邮电出版社，1988.

［3］Michel Aguet，Mircea Ianovici，Lin Chung-chi.Transient electromagnetic field coupling to long shielded cables［J］.IEEE Transactions on Electromagnetic Compatibility，1980，10(4):276-282.

［4］D’Amore M，Feliziani M.EMP coupling to coaxial shielded cables［C］.IEEE International Symposium on Electromagnetic Compatibility，1988，37-44.

［5］D’Amore M，Feliziani M.Induced fast transients in multionductor shielded cables［C］.Seventh International Conference on EMC，1990，103-108.

［6］Celozzi S，Feliziani M.EMP coupling to twisted-wire cables［C］.IEEE International Symposium on EMC，1990，85-89.

［7］Arlon T Adams，Jose Perini，Masahiro Miyabayashi，et al.Electromagnetic field-to-wire coupling in the SHF frequency range and beyond［J］.IEEE Transactions on Electromagnetic Compatibility，1987，10(2):126-131.

［8］Tesche F M，Ianoz M V，Karlsson T.EMC analysis methods and computational models［C］.John Wiley ＆ Sons，New York，1999.

［9］Beilfuss J，Bell A，Gray B，et al.Multiconductor cable response dependency on propagation modes［C］.IEEE International Symposium on EMC，1988，118-123.

［10］Kley T.Measuring the coupling parameters of shielded cables［J］. IEEE Transactions on Electromagnetic Compatibility，1993，35(1):10-20.

［11］Helmers S，Gonschorek K H.On the contribution of transfer admittance to external field coupling into shielded cables［C］.IEEE International Symposium on Electromagnetic Compatibility，1999，vol.1:206-211.

［12］Orlandi A.Full SPICE model for transfer impedance and transfer admittance inclusion in shield ed coaxial cables analysis［J］.IEEE Proceedings Science，Measurement and Technology，2003，150(6):297-306.

［13］Levin B M.Calculation of electrical parameters of two-wire lines in multiconductor cables［J］.IEEE Transactions on Electromagnetic Compatibility，2008，50(3):697-703.

［14］Sabrina Mezoued，Bachir Nekhoul，Kamel Kerroum，et al.A new formalism for the analysis of electromagnetic coupling between the lightning and a complex network of lines on electromagnetic or cables［C］.International Symposium Compatibility-EMC Europe，2008，1-7.

［15］姜仁波.多导体传输线电磁兼容的分析与研究［D］.北京:华北电力大学，2004.

［16］孙蓓云，周 辉，田吉波，等.多导体屏蔽电缆耦合效应研究［J］.核电子学与探测技术，2003，23(3):246-249.

［17］王泽忠，李云伟，卢斌先，等.变电站电磁脉冲耦合倾斜二次电缆数值分析［J］.高电压技术，2007，33(7):98-101.

［18］齐 磊，卢铁兵，崔 翔.基于时域有限差分法的非均匀多导体传输线瞬态分析［J］.中国电机工程学报，2002，23(7):102-106.

［19］齐 磊，崔 翔，卢铁兵，等.屏蔽电缆的分布参数测量及瞬态分析［J］.中国电机工程学报，2005，25(6):119-123.

［20］卢铁兵.变电站瞬态电磁环境数值预测方法的研究［D］.保定:华北电力大学，2002.

［21］陈炜峰，景萃慧，张丙伟.EMP作用下的电缆耦合及屏蔽效能试验分析［J］.电力电子技术，2007，41(12):5-7.

［22］张志军.电磁脉冲对传输线耦合规律的研究［D］.北京:华北电力大学，2006.

［23］陈 彬，王廷永，高 成，等.电磁脉冲作用下近地电缆外皮感应电流的全波分析［J］.微波学报，2000，16(5):549-553.

［24］马 良，周 辉，程引会，等.地面铺设缆线的高空电磁脉冲响应研究［J］.强激光与粒子束，2008，20(3):464-468.

［25］张 刚，王立欣，刘 超.一种求解屏蔽电缆场线耦合问题的混合方法［J］.电工技术学报，2010，25(5):9-13.

［26］刘素玲，李 霞，沈远茂，等.外场激励时通信电缆的瞬态响应分析［J］.河北大学学报自然科学版，2008，28(1):96-100.

［27］刘顺坤，陈雨生，孙蓓云，等.电磁脉冲作用下地面铺设屏蔽电缆蒙皮电流分布的时域计算方法研究［J］.强激光与粒子束，2005，17(2):283-286.

［28］谢彦召，王赞基，王群书，等.架空多导体传输线缆的电磁脉冲响应计算［J］.清华大学学报(自然科学版)，2006，46(4):449-452.

［29］李 莉，万里兮，咸金龙，等.多导体传输线互耦实验研究［J］.电波科学学报，1999，14(2):166-171.

［30］陶苏东.转移阻抗的计算方法［J］.山东电力技术，2003，(3):73-75.

［31］杨进候，王志杰，许 军.导体传输线间的高频耦合干扰模型［J］.鱼雷技术，2005，13(3):18-20.

［32］门秀花，李舜酩，占日新.用于多导体传输参数提取的等效电流密度法［J］.西安交通大学学报，2008，42(12):1522-1525.

［33］孙秀英，于正永.带状多导体传输线的特性参数提取［J］.大众科技，2009(6):55-56.

［34］衣 斌.空间电磁脉冲作用下屏蔽电缆的耦合规律研究［D］.保定:华北电力大学，2008.

［35］刘 波，高本庆.电磁场时域数值方法及其混合技术概述［J］.微波学报，2006，22(2):1-5.

［36］Chen Zhizhang，Ney M M，et al.A new finite-difference timedomain formulation and its equivalence with the TLM symmetrical condensed node［J］.IEEE Trans.Microwave Theory Tech.，1991，39(12):2160-2169.

［37］Hang Jin and Vahldieck R.Direct derivations of TLM symmetrical condensed node and hybrid symmetrical condensed node from Maxwell’s equations using centered differencing and averaging［J］.IEEE Trans.Microwave Theory Tech.，1994，MTT242(12):2554-2560.

［38］邵振海，洪 伟.一种新的压缩顶点传输线矩阵法及其应用［J］.电波科学学报，1999，14(4):426-433.

［39］Helmers S，Donschorek K H.On the contribution of transfer admittance to external field coupling into shielded cables［C］.IEEE International Symposium on EMC，1999，Volumel:2-6.

［40］Tesche F M，Ianoz M V，Karlsson T.EMC analysis methods and computational models［C］.New York:John Wiley ＆ Sons，1999.

［41］［加］Dommel.H.IV著，李永庄等译.电力系统电磁暂态计算理论［M］.北京:水利电力出版社，1991.