改进的混合蛙跳算法求解背包问题

陈 亮

(泰山职业技术学院信息工程系，山东泰安 271000)

0 引 言

混合蛙跳算法(shuffled frog leaping algorithm，SFLA)是2000年由Eusuf和Lansey受青蛙群体觅食的行为启发，并总结其规律而提出的一种基于群体智能的后启发式仿生算法[1]。该算法将全局信息交换和局部深度搜索相结合，通过局部搜索使得信息能在局部个体间传递，其采用的混合策略能使得局部信息在全局范围内得以传递[2]。

1 背包问题

背包问题(knapsack problem)是一种组合优化的NP完全问题，通常背包问题分为0/1背包问题、完全背包问题、多重背包问题、混合背包问题4种，由于后3种可以转化为第一种，因此，文中只讨论0/1背包问题[3]。

0/1背包问题的数学模型描述为:

式中:n——物体个数;

w i——第i种物品的重量(i=1，2，…，n);

vi——第i种物品的价值;

xi——第i种物品的选择状态，当物件i被选入背包时，定义变量xi=1或0;

C——背包的最大容量。

2 混合蛙跳算法基本流程

随机生成P只青蛙，每只青蛙代表一个问题的解，记为Ui，并视为初始族群。然后计算族群内所有的青蛙的适应度，并将青蛙按适应度降序排列，再将整个族群内的青蛙分成m个子族群，每个子族群包含n只青蛙，因此满足关系P= m*n。分配方法:按排定顺序把第1，2，…，n只青蛙分别分到第1，2，…，n个子族群中，第a+1只青蛙分到第1个子族群中，依次类推，直至全部青蛙分配完毕[4]。

对于每一个族群，设UB为适应度最好的解，UW为适应度最差的解，U g为所有族群中具有全局最好适应度的解。然后对每个族群进行局部深度搜索，并对局部最优解进行更新，更新策略为[5]:

式中:S——青蛙个体的调整矢量;

S max——青蛙个体允许改变的最大步长;

rand——0和1之间的随机数。

3 基于混合蛙跳算法的0/1背包问题求解

3.1 青蛙个体向量表示

一只青蛙代表一个解，用物体选择状态向量表示，则青蛙U=(x1，x2，…，xn)，其中xi表示第i个物体的选择状态。即xi=1，表示选中第i个物体;xi=0，表示未选中第i个物体。青蛙个体适应度函数f(i)定义为:

3.2 子族群的构造

在构造子族群时，根据适应度的大小进行青蛙选择，即适应度较大，选择权重越大，越有机会选中加入到子族群中。按概率选择青蛙进行子族群的构造，概率公式定义为[6]:

且

式中:pi——第i只青蛙被选中的概率;

n——每个族群中青蛙个数。

3.3 青蛙个体的更新策略

定义1 给定一个青蛙向量U，定义交换序C(i，j)为:

式中:Ui变值 ——物品i由选中状态变为取消状态，或相反;

Ui=Uj——物品i与物品j交换位置，即物品i与物品j同为选中或取消状态;

Ui≠Uj——选中物品i且取消物品j，或相反。

则交换操作的新向量

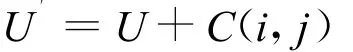
定义2 在族群中任意选两只青蛙的向量Ui，U j，由U i调整到U j的所有交换序列称为U i到U j的距离D:

式中:m——调整的次数。

定义3 在族群中任意选两只青蛙的向量Ui，U j，由U i调整到U j的距离长度为|D|

式中:m——调整的次数。

由以上定义确定青蛙个体的更新策略如下:

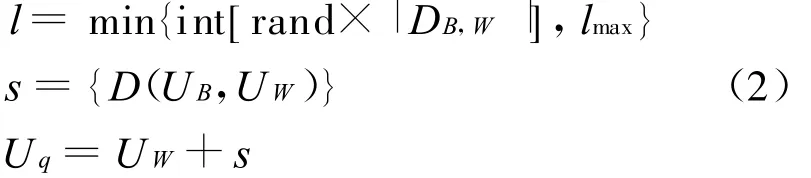
式中:l——更新UW选择用交换的D(UB，UW)交换序的个数;

lmax——允许选择的最大交换序的个数;

s——更新UW所需的交换序列。

3.4 全局信息交换策略

在基本混合蛙跳算法执行过程中更新可行解的操作反复被执行，不可避免地遇到更新失败的情况，基本的混合蛙跳算法采用了随机更新可行解的方法，但随机方法经常会陷入局部最优或使算法的收敛速度降低。文中引入高斯变异算子以修正更新策略，即用高斯变异算子对子族群最差青蛙(可行解)进行扰动，即:

式中:Rand——高斯随机分布函数。

新的更新策略在整个迭代过程中将提高群体的多样性和最差个体搜索的遍历性，可以确保群体持续进化，有利于提高收敛速度，并避免陷入局部最优，进而期望算法既能快速收敛到最优解的附近，又能比较好地逼近精度，改进了混合蛙跳算法的性能。

3.5 算法描述

步骤1:初始化青蛙族群，并生成初始子族群。

步骤2:按式(1)计算每只青蛙的适应度，并按降序排序。

步骤3:搜索出全局最优可行解Ug、子族群最优可行解UB和最差可行解UW。

步骤6:更新完成后，对所有子族群的所有青蛙重新进行混合，形成新的族群。

步骤7:输出Ug。

4 实验结果分析

采用两个经典0/1背包问题实例，实例1选自文献[7]，实例2选自文献[8]。采用的对比算法为0/1背包问题分支限界法。在相同实验条件下对两个实例分别进行20次仿真实验，统计其平均实验结果，见表1。

表1 实验结果

经过分析实验结果，两种算法执行结果相同，混合蛙跳算法的执行速度有较大提高，因此，混合蛙跳算法是有效、可行的。

5 结 语

混合蛙跳算法是一种具有随机智能和全局搜索能力的搜索算法，文中应用混合蛙跳算法解决了0/1背包问题求解。实验证明，混合蛙跳算法在解决0/1背包问题上具有较好的可行性和有效性，采用高斯变异算子有效避免了易陷入局部最优的缺陷，在一定程度上提高了算法的收敛速度。

[1] 罗雪晖.改进混合蛙跳算法求解旅行商问题[J].通信学报，2009，7(7):130-134.

[2] 周丽娟.改进粒子群算法和蚁群算法混合应用于文本聚类[J].长春工业大学学报:自然科学版，2009，30(3):281-284.

[3] 吴哲辉.算法设计与分析[M].北京:高等教育出版社，1993:248-249.

[4] 罗雪晖.基于混合蛙跳算法的背包问题求解[J].科学技术与工程，2009，8(15):4364-4365.

[5] 骆剑平，李霞.求解TSP的改进混合蛙跳算法[J].深圳大学学报，2010，4(2):173-177.

[6] 栾壶琛.混洗蛙跳算法研究及其发展现状[J].大众科技，2009(1):24-26.

[7] 贺毅朝.求解背包问题的贪心遗传算法及其应用[J].计算机工程与设计，2007，28(11):19-22.

[8] 吴哲辉.算法设计与分析[M].北京:高等教育出版社，1993:251-152.