非线性滤波在捷联惯导系统初始对准中的应用

戴邵武，郑智翔，戴洪德，曹亮杰

（海军航空工程学院 a.控制工程系；b.研究生管理大队，山东 烟台 264001）

0 引言

初始对准作为惯性导航系统的关键技术之一，对准精度直接影响导航系统的精度。当失准角为小角度时，捷联惯导系统（SINS）的误差方程可近似为线性方程，并可采用卡尔曼滤波估计SINS 失准角；当运载体遭遇恶劣环境，姿态变化剧烈，此时利用粗对准得到的初始姿态误差将非常大，基于小失准角的系统误差模型已经不能准确地描述惯性导航系统的误差传播特性，则需引入大失准角误差方程，以减少初始对准中的非线性误差。

本文主要研究SINS 初始对准中大失准角的滤波问题。文中首先建立基于大失准角的SINS 误差模型，接着介绍2种非线性滤波——Unscented卡尔曼滤波（UKF）和Unscented粒子滤波（UPF），然后对误差模型进行仿真分析。仿真结果表明，在大失准角下的初始对准中，UPF较 UKF 具有更理想的滤波效果。

1 捷联惯导系统非线性误差模型

合理、准确的惯导系统误差模型，可以提高初始对准精度，缩短对准时间。惯性导航系统的误差模型本质上是非线性的，与线性误差模型相比，非线性误差模型不仅能更准确地描述误差的传播特性，而且由于不需要很多约束条件，可以进一步扩展误差模型的应用范围。下面将建立大方位失准角情况下的非线性初始对准模型。

首先，通过加速度计和陀螺敏感地球重力g和地球自转角速率ωie的信息，估算载体坐标系到地理坐标系的变换阵；然后，再精确估计计算地理坐标系与真实地理坐标系之间的失准角ϕ，从而建立起准确的初始变换矩阵，使计算地理坐标系与实际地理坐标系重合，完成捷联惯导系统的初始对准。对准中，从地理坐标系 (t)到计算平台系 (p)的转换矩阵为：

因此，姿态误差方程可表示为[1]：

速度误差方程可表示为：

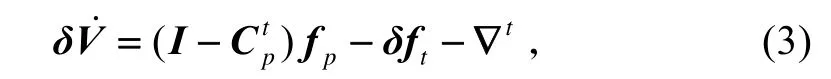
由于垂直通道与两个水平通道的耦合很小，因此将垂直通道略去，即不考虑 Uvδ的影响。不考虑位置误差，因此可得到静基座大方位失准角时的速度误差方程和姿态误差方程为[1]：

则根据式(4)以及(2)和(3)可得到初始对准的非线性系统方程：

式中：v为系统噪声，假设为独立高斯分布。

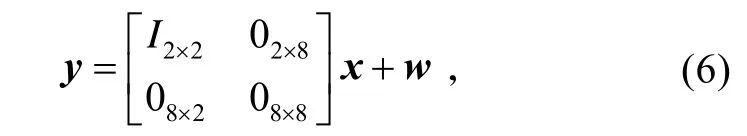
式中：w为量测噪声，假设为独立高斯分布。

2 UKF算法及实现

扩展卡尔曼滤波应用于非线性系统的状态估计得到了学术界和工程界的普遍认可，但由于EKF 将动力学模型在当前状态估计值处进行Taylor 展开线性化，并将量测模型在状态一步预测处进行Taylor展开线性化，仅近似到非线性函数Taylor 展开式的一次项，在估计状态后验分布的统计特性时会产生较大误差。

为改善非线性滤波效果，S.J.Juliear 等提出了基于UT（Unscented Transformation）采样的卡尔曼滤波方法（UKF）。[2-3]

在UKF中，状态分布同样为高斯分布，其特性由一组确定选择的采样点给出。这些采样点能完全捕获高斯分布变量的均值和方差，通过真实非线性系统的传播后，其捕获的均值和方差能精确到任意非线性的Taylor 展开的二次项。

设随机非线性系统的状态空间模型为：

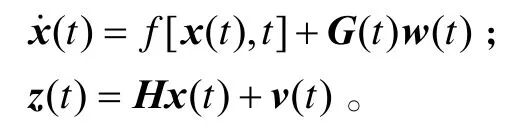
该系统的UKF算法为：

1）计算Sigma点：

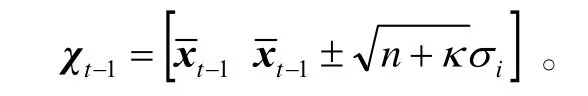
2）时间更新：

3）量测更新：

显然，实现UKF 不需要计算Jacobian 矩阵，也不需要对系统方程和量程方程线性化。

3 Unscented粒子滤波

粒子滤波[4]（PF）是一种序列蒙特卡罗滤波方法，它通过对一组随机采样的加权粒子演化与传播来递推近似状态的后验概率密度函数，从而获得其他关于状态的统计量。从理论上来说粒子滤波可以应用于任何动态状态空间模型，是一种最优的非线性滤波器。

对于服从p(x)分布的非线性系统f(x)，从中采样一定数量的粒子（N为粒子数量）来表示概率密度函数，有

式中：δ (⋅)为Dirac delta函数；1/N为对应的权值，故可得f(x)的期望估计值为

对状态方程是非线性，观测方程是线性的非线性系统离散化，可写成

粒子滤波中，权值较小的粒子随运算的进行而很快消失，权值大的粒子得以保留，这种粒子衰竭的现象严重影响了粒子滤波的性能。

采用重采样可有效遏制粒子的衰竭，保持粒子的平衡，重采样后粒子对应的权值wk,i均被重新定义为1/N。

确定了k时刻的粒子值与对应的归一化权值，则系统状态最优估计值为

设非线性系统过程噪声的方差为Q，观测噪声的方差为R，综合Unscented卡尔曼滤波和粒子滤波，Unscented粒子滤波算法如下[6-7]：

1）在t=0时刻，从 x0～ p(x0)中采样N个粒子x0,i(i=1,2,…,N)对非线性系统初始化：

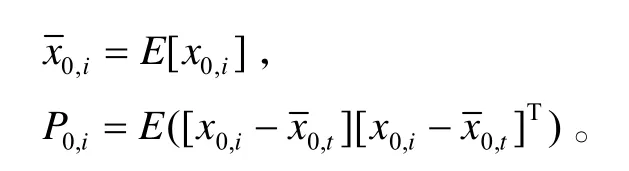
2）i=1,2,…,N时刻，在每个时刻，对每个粒子进行如下运算：

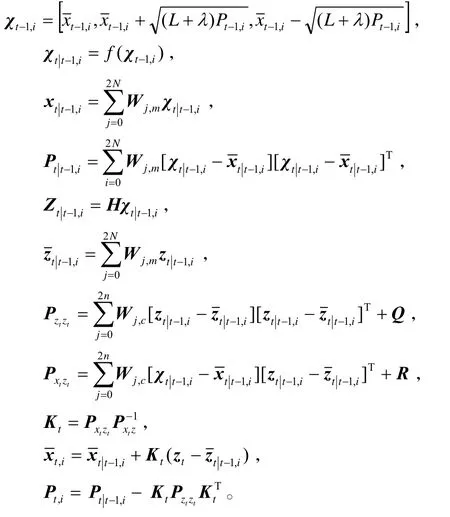
3）利用重采样算法，对加权粒子进行重采样；

4）计算非线性状态量估计值；

5）返回第2）步，按新观测量递归计算下一个时刻的状态估计量。

4 仿真

对某捷联惯导系统进行初始对准，状态矢量x的初始值X(0)均取0，初始失准角 φE=φN=1°，φU=10°，陀螺常值漂移为0.02 (°)/h，随机漂移为(1.0×10−3(°)/)2，加 速 度 计的初 始 偏 差为1.0×10−4m/s2，随机偏差为(1.0×10−5m/s3/2)2，速度测量误差为0.01 m/s，安装误差为10′，当地地理纬度为北纬 40 °，初始状态采样的粒子服从p(x(0))～N(x(0),P0)。则P0、Q、R为

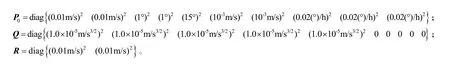
给定初始状态为

从重要性函数中采样的粒子数N=100，分别用Unscented卡尔曼滤波和Unscented粒子滤波进行对准，结果如图1～3所示：

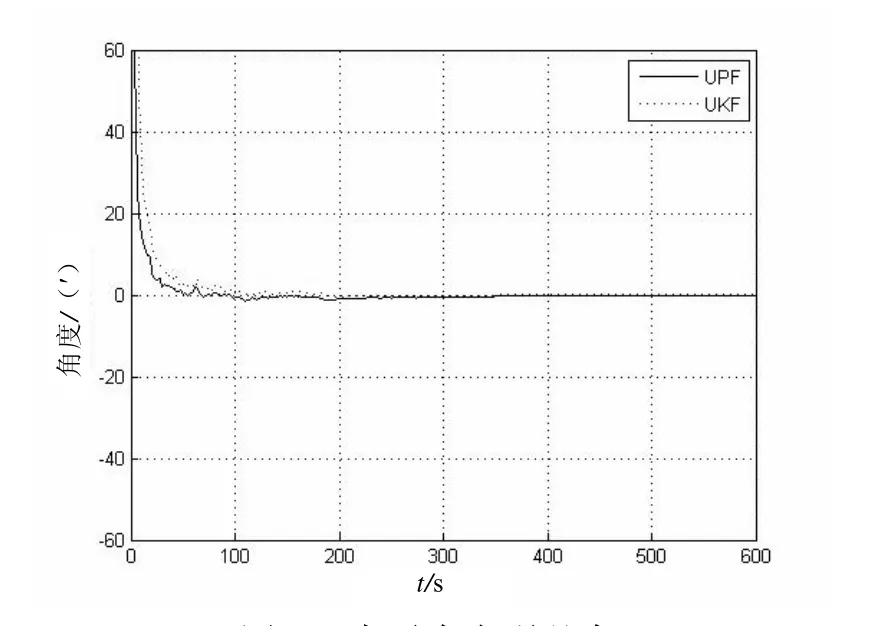
图1 水平东向误差角

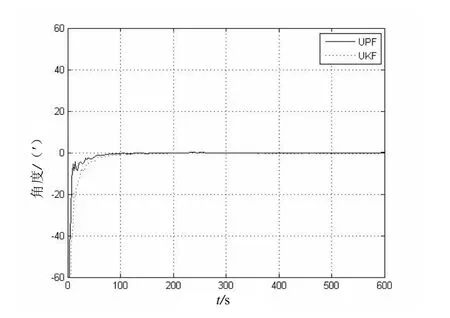
图2 水平北向误差角

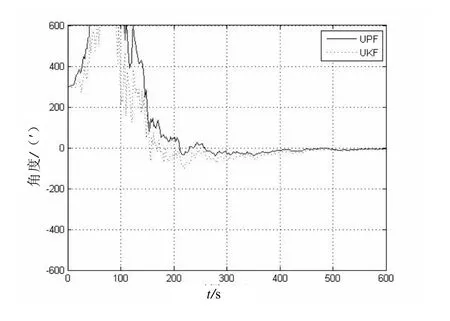
图3 方位误差角

从图1、图2中可以看出，用Unscented卡尔曼滤波和Unscented粒子滤波对水平角的对准均能快速收敛至稳态值，对准误差也快速收敛到了稳态值。显然，在大方位失准角对准中，利用Unscented粒子滤波处理达到稳态值的速度比用Unscented卡尔曼滤波处理达到稳态值的速度要快。在图3方位角对准误差图中可以看出Unscented粒子滤波误差减少速率比Unscented卡尔曼滤波减少速率快，其中Unscented粒子滤波达到的稳定对准误差是2.05′，而 Unscented卡尔曼滤波达到的稳定对准误差是2.17′，理论的稳定对准精度是1.97′。由此比较可以看出，应用Unscented粒子滤波对准的精度比Unscented卡尔曼滤波对准的精度要高。

5 结论

对Unscented卡尔曼滤波和Unscented卡尔曼粒子滤波在捷联惯导系统大方位失准角初始对准进行了研究，利用Unscented卡尔曼滤波和Unscented卡尔曼粒子滤波对静基座大方位失准角捷联惯导系统初始对准进行分析和仿真。结果证实了两种非线性滤波的可行性，且Unscented卡尔曼粒子滤波在初始对准中效果优于Unscented卡尔曼滤波。

[1]赵瑞.捷联惯导系统自动标定和初始对准的理论和实验研究[D].北京∶清华大学,2001∶58-118.

[2]JULIER S J,UHLMAN J K.A new approach for filtering nonlinear systems[C]//Proceedings of the 1995 American Control Conference.Seattle,W A∶[s.n.],1995∶1628-1632.

[3]JULIER S J,UHLMANNN J K.A new method for the nonlinear transformations of means and covariances in filters and estimator[J].IEEE Trans A C,2000∶45(3)∶477-482.

[4]GORDON N J,SALMOND D J,SMITH A F M.Novel approach to nonlinear/non-gaussian bayesian state estimation[J].IEEE Proceedings of Radar and Signal Processing,1993∶140(2)∶107-113.

[5]朱志宇.粒子滤波算法及其应用[M].北京∶科学出版社,2010∶25-26.

[6]MERWE R V,DOUCET A,DE FREITAS N,et al.The unscented particle filter[R]//Technical Report CUED/F-INPENG/TR 380.Cambridge University Engineering Department,2000.

[7]秦永元.惯性导航[M].北京∶科学出版社,2006∶7-8.

[8]雄凯,张洪钺.粒子滤波在惯导系统非线性对准中的应用[J].中国惯性技术学报,2003,11(6)∶20-22.