磁探仪应召搜潜建模与仿真

蒋志忠，杨日杰，熊 雄，沈 阳

（海军航空工程学院电子信息工程系，山东 烟台 264001）

0 引言

磁探仪是反潜机、尤其是反潜巡逻机装备的主要反潜探测设备，具有分类能力好、定位精度高、受浅海复杂水文气象环境影响较小等优点[1]。主要用于应召搜潜，即在知道潜艇的概略位置后，反潜巡逻机飞往潜艇初始位置，根据潜艇运动态势进行一定的战术飞行，以便再次与潜艇发生接触。但磁探仪的有效作用距离较短，而反潜巡逻机利用磁探仪进行搜索时的飞行速度较快，机动能力较弱。为了有效的对潜艇进行再次搜索，必须对反潜巡逻机利用磁探仪执行应召搜潜的飞行航路进行规划。而目前国内外对这方面进行的研究工作还较少，仅在战术上对磁探仪应召搜潜进行了定性描述或者在理论上进行了一定研究[2-8]，缺乏必要的模型支持和仿真验证。为此，本文根据磁探仪应召搜潜战术，结合某型反潜巡逻机本身机动能力，建立反潜巡逻机利用磁探仪执行应召搜潜的模型，并进行了仿真分析。

1 反潜巡逻机利用磁探仪执行应召搜潜航路规划的数学模型

反潜巡逻机利用磁探仪执行应召搜潜的方法主要有平行航线、扩展矩形和螺旋形[2-8]。

因为反潜巡逻机在巡航过程中和搜潜过程中，其飞行高度基本不变，忽略从巡航高度下降到搜潜高度的过渡过程，故只需建立二维航路规划模型。根据磁探仪应召搜潜方法，结合基于关键点飞行线路模拟算法[9]，可建立反潜巡逻机在二维直角坐标系下的航路规划的数学模型。

1.1 平行航线搜潜航路规划数学模型

已知：反潜机的初始位置 (P la_x0,Pla_y0)，巡航速度 vcse，利用磁探仪搜潜时的飞行速度vsch，飞行高度H，初始航向 α0，最大转弯坡度角为ω；潜艇初始概略位置 (S ub_x0,Sub_y0)，潜艇经济航速 vse，潜艇下潜深度h；所在海域重力加速度为g，磁探仪作用距离为dMAD。

设反潜巡逻机以巡航速度飞行时的最小转弯半径为R1，以搜潜速度飞行时的最小转弯半径为R2，磁探仪的搜索宽度为W，则有：

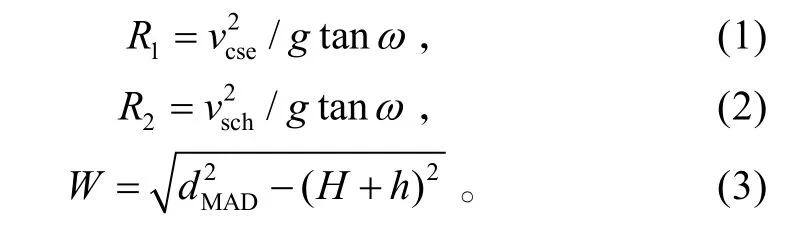
平行航线搜潜航路如图1所示。图1中，Pi为关键点，其中P1为反潜巡逻机初始位置；O为潜艇初始概略位置；r为反潜巡逻机从P1飞到O延迟时间内潜艇可能逃逸的范围半径；D为航线间距，取D=W；ϕ为目标方位角。

图1 平行航线搜潜航路

令Pi的航向为αPi，Pi→Pi+1的时间为Ti，航线长为Li，则αP1=α0。

平行航线搜潜航路可分为14个过程，即P1→P2→P3→P4→P5→P6→P7→P8→P9→P10→P11→P12→P13→P14→P15，之后根据搜潜范围以P3→P4→P5→P6→P7→P8→P9→P10→P11→P12→P13→P14→P15为一个飞行周期。

1）P1顺时针盘旋转弯飞到P2。

当0≤t≤T1时，

到达P2时，

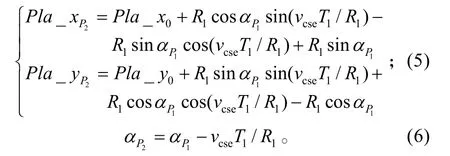
又此时飞机航向等于切线矢量P2P3的方向，即

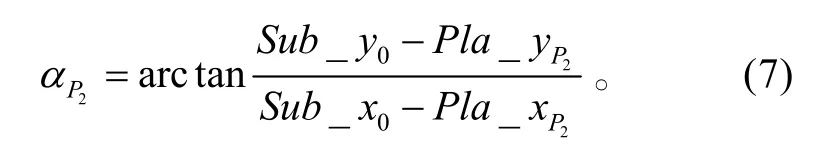
联立式(5)～(7)可求解1T。

2）P2直飞到P3。

由图1可知：

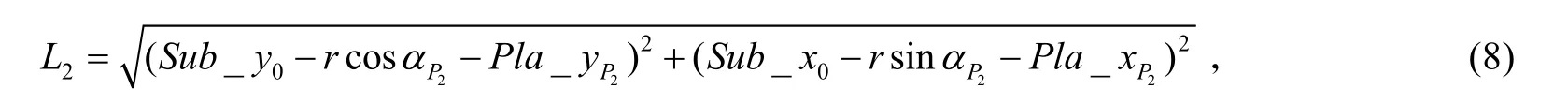
则T2=L2/vcse，当0≤t≤T2时，

3）P3直飞到P4。

由图1可知：

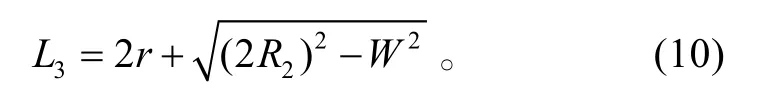
建模方法与第2）过程相同。

4）P4逆时针盘旋转弯飞到P5。

T4=(π/2) R2/vsch，则当0≤t≤T4时，

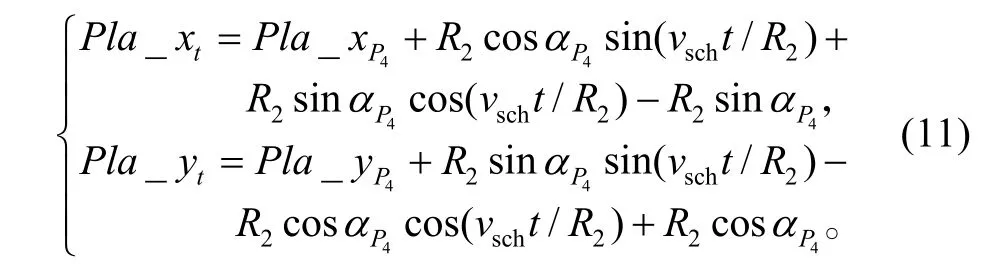
5）P5直飞到P6。

设P5到P6的距离为S1，S1=0，之后根据循环次数每次增加2W，即Si+1=Si+2W，i=1,2,…,p，p为循环次数，

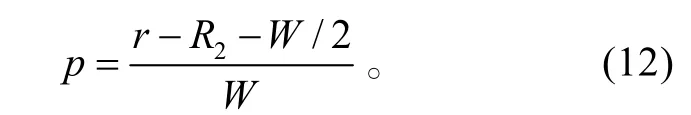
建模方法与第2）过程相同。

6）P6逆时针盘旋转弯飞到P7。

T6=(π/2) R2/vsch，建模方法与第4）过程相同。

7）P7逆时针盘旋转弯飞到P8。

8）P8顺时针盘旋转弯飞到P9。

9）P9直飞到P10。

由图1可知：

建模方法与第2）过程相同。

10）P10逆时针盘旋转弯飞到P11。

T10=(π/2) R2/vsch，建模方法与第4）过程相同。

11）P11直飞到P12。

建模过程与第5）过程完全相同。

12）P12逆时针盘旋转弯飞到P13。

建模过程与第6）过程完全相同。

13）P13逆时针盘旋转弯飞到P14。

建模过程与第7）过程完全相同。

14）P14顺时针盘旋转弯飞到P15。

建模过程与第8）过程完全相同。

1.2 扩展矩形搜潜航路规划数学模型

已知条件与平行航线搜潜相同，扩展矩形搜潜航路如图2所示。

图2 扩展矩形搜潜航路

由图2可知，扩展矩形搜潜航路可分为10个过 程，P1→P2→P3→P4→P5→P6→P7→P8→P9→P10→P11，之后根据搜潜范围以 P3→P4→P5→P6→P7→P8→P9→P10→P11为一个飞行周期。

P1→P2→P3的建模过程与平行航线建模相同。

P3→P4和P7→P8为直飞过程，直飞段长度为r。

P4→P5、P6→P7、P8→P9和P10→P11为逆时针盘旋转弯过程，转过的角度均为π/2。

P5→P6为直飞过程，设直飞段长度为S1，则S1=r−2 R2−W/2；P9→P10为直飞过程，设直飞段长度为S2，则S2=S1+D。

1.3 螺旋形搜潜航路规划数学模型

已知条件与平行航线搜潜相同，螺旋形搜潜航路如图3所示。

由图3可知，螺旋形搜潜航路可分为8个过程，P1→P2→P3→P4→P5→P5→P6→P7→P7，之后根据搜潜范围以 P5→P5→P6→P7→P7为一个飞行周期。

P1→P2→P3的建模过程与平行航线建模相同。

P3→P4为逆时针转弯过程，转过的角度为3π/2。

P4→P5为直飞过程，直飞段长度为R2。

P5→P5为逆时针转弯过程，转过的角度为2π。

P5→P6为直飞过程，直飞段长度为D。

P6→P7为逆时针转弯过程，转过的角度为π/2。

P7→P7为逆时针转弯过程，转过的角度为2π，转弯半径为R2+W。

图3 螺旋形搜潜航路

2 潜艇运动模型

应召搜潜时，可以认为潜艇初始位置服从以初始概略位置为均值，以初始散布为标准差的正态分布，航速服从以经济航速为均值的瑞利分布[10]；可以将潜艇的运动模型归纳为4类[11-12]：

模型1：潜艇运动过程中，航速航向都保持恒定；

模型2：潜艇运动过程中，航向恒定航速变化；

模型3：潜艇运动过程中，航速恒定航向变化；

模型4：潜艇运动过程中，航向航速都变化。

改变航向时的回旋半径按满舵时计算，对常规潜艇，一般取15 yd[13]。

当t∈ [0,Δ ti]，即潜艇在第i个时间段内时，潜艇任意时刻的位置为：

潜艇第i+1个时间段的起始位置可表示为：

3 仿真分析

设反潜巡逻机正在海上巡逻，接到命令后前往潜艇初始概略位置，执行平行航线、扩展矩形和螺旋形搜潜。根据蒙特卡罗法的基本思想（从统计学的角度计算搜潜概率），对反潜巡逻机利用磁探仪搜索潜艇的随机事件做统计试验。仿真比较这3种搜索方法在同一潜艇运动模型条件下，不同的潜艇初始位置散布、不同的初始距离、不同的潜艇经济航速以及不同海洋环境磁噪声对搜潜概率的影响。

3.1 仿真条件假定

1）当接到命令后，反潜巡逻机飞往潜艇初始概略位置利用磁探仪进行应召搜潜，以接到命令时刻作为时间起点。

2）搜索区内有且只有1 艘潜艇在活动，潜艇和反潜巡逻机行动各自独立，且潜艇下潜深度始终在磁探仪作用范围之内。

3）在已知海洋环境条件下，磁探仪的战术作用范围是以反潜巡逻机在海面的投影为圆心，以磁探仪的搜索宽度的一半为半径的圆，当目标位于探测圆内时则发现潜艇，否则不能发现目标。

3.2 仿真步骤

1）输入初始条件。包括反潜巡逻机的初始位置、巡航速度和航向、利用磁探仪搜潜时的飞行速度、最大转弯坡度角；根据海况选择反潜巡逻机的飞行高度和磁探仪的有效作用距离；潜艇的初始概略位置、潜艇下潜深度、潜艇经济航速、初始概略位置的散布；所在海域重力加速度。

2）产生正态分布的潜艇初始位置，产生瑞利分布的潜艇航速。

3）根据潜艇运动模型计算潜艇的位置(Sub_xt,,Sub_yt)，根据反潜巡逻机的航路规划模型计算反潜巡逻机的位置(Pla_xt,Pla_yt)。

4）判断搜潜过程中，潜艇位置与反潜巡逻机的位置是否满足：

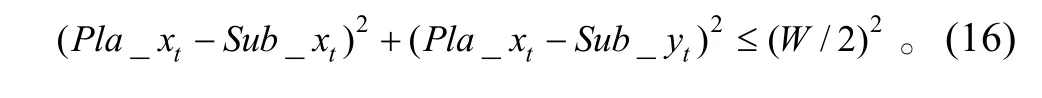
整个搜潜过程如果满足上式，则记下捕获目标一次，并退出本次循环，进入下一次循环；如果不满足上式，则执行完整个过程，再进入下一次循环，重复执行第2）、3）和4）步，直到最大循环数。

5）统计得到搜潜概率，假设捕获目标的次数为m，总的循环次数为N，则搜潜概率P 定义：

3.3 仿真结果与分析

影响搜潜概率的主要因素有潜艇初始位置散布、反潜巡逻机与潜艇之间的初始距离、潜艇经济航速和海洋环境磁噪声。

前3个因素直接影响搜潜范围，从而影响搜潜概率，后1个因素直接影响磁探仪作用距离，从而影响搜潜概率。

磁探仪的作用距离大小会直接影响其搜潜概率，它不仅和自身性能有关，与海洋环境也有密切关系。由参考文献[14]可知磁探仪的实时作用距离为：

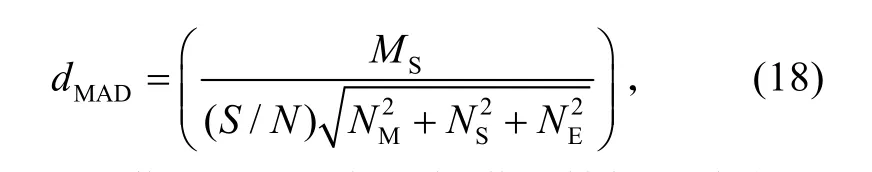
式中：MS为潜艇磁距，与目标潜艇结构尺寸大小和消磁水平，以及航行方向有关；S/N为达到一定检测概率所需信噪比；NM为磁探仪探头因飞机运动产生的动态噪声；NS为磁探仪设备的静态噪声；NE为海洋磁环境噪声。

对具体型号的磁探仪，其动态噪声和静态噪声是常数，由磁探仪有效作用距离估算模型可知，磁探仪的有效作用距离决定于海洋环境磁噪声，而海洋环境磁噪声主要与海况有关[15]，如已知特定海况下的海洋环境磁噪声及磁探仪的有效作用距离，则可估算出磁探仪任意海况下的实时作用距离。

假设3级海况时，磁探仪作用距离为dMAD0，海洋环境磁噪声为N0，则任意海洋环境磁噪声情况下的磁探仪作用距离为：

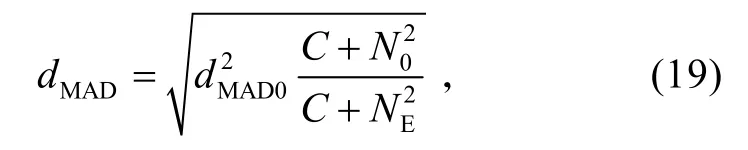
仿真11类模型条件下，各要素对搜潜概率的影响。

仿真参数：仿真次数10 000，地面重力加速度为9.8 m/s2；反潜巡逻机的初始位置(200,200) km，反潜巡逻机巡航速度为600 km/h，初始航向为150°，最大转弯坡度角为30°，根据参考文献[16]，利用磁探仪搜潜时的速度取300 km/h，飞行高度取100 m；根据参考文献[17]，常规潜艇的经济航速取10 km/h，潜艇下潜深度50 m；根据参考文献[18]，3级海况时，磁探仪有效作用距离取500 m。

当潜艇初始位置散布为0.1～1 km；潜艇初始位置为(200+d,200+d) km，d 取50～150 km；潜艇经济航速为6～36 km/h；dMAD0=500 m，N0=0.03 nT，NM=0.02 nT，NS=0.016 nT，NE为0.01～0.09 nT时，仿真结果如图4所示。

图4 1类模型条件下各要素对搜潜概率的影响

由图4可知，1类模型条件下，相同潜艇初始位置散布、初始距离、潜艇经济航速和海洋环境磁噪声时，螺旋形搜潜概率明显高于平行航线和扩展矩形搜潜概率，且螺旋形搜潜概率受各要素影响相对较小。此外，由3种搜潜方法的航路规划模型可知，相同搜潜范围时，螺旋形搜潜时间要小于平行航线和扩展矩形所需搜潜时间。因此，螺旋形的搜潜效能明显高于平行航线和扩展矩形的搜潜效能。

仿真22类模型条件下，各要素对搜潜概率的影响。

仿真参数不变，仿真结果如图5所示。

由图5可知，2类模型条件下，相同潜艇初始位置散布、初始距离、潜艇经济航速和海洋环境磁噪声时，搜潜概率明显下降；潜艇经济航速为6～12 km/h时，螺旋形搜潜概率略高于平行航线与扩展矩形搜潜概率，潜艇经济航速为12～36 km/h时，螺旋形搜潜概率略低于平行航线与扩展矩形搜潜概率。

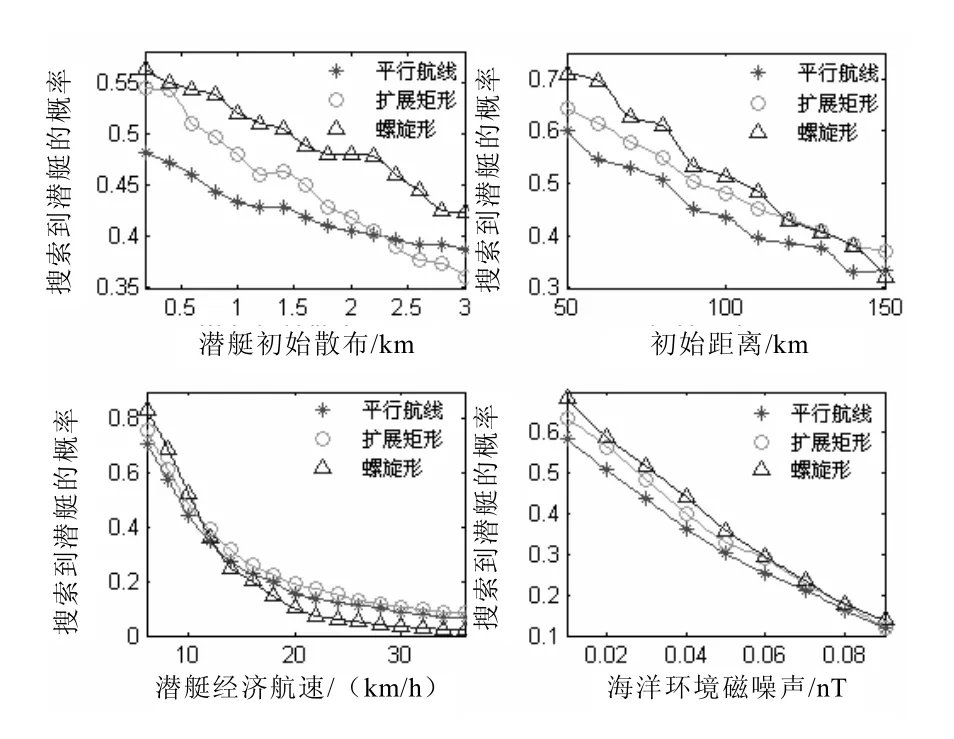
图5 2类模型条件下各要素对搜潜概率的影响

仿真33类模型条件下，各要素对搜潜概率的影响。

仿真参数不变，仿真结果如图6所示。

图6 3类模型条件下各要素对搜潜概率的影响

由图6可知，3类模型条件下，当潜艇初始散布为0.2～0.6 km时，螺旋搜潜概率小于平行航线和扩展矩形搜潜概率；当潜艇初始散布为0.6～3 km时，螺旋搜潜概率大于平行航线和扩展矩形搜潜概率；相同条件下，平行航线和扩展矩形搜潜概率明显提高。

仿真44类模型条件下，各要素对搜潜概率的影响。

仿真参数不变，仿真结果如图7所示。

由图7可知，4类模型条件下，当潜艇初始散布为0.2～1 km时，螺旋形搜潜概率增加，当潜艇初始散布为1～3 km时，螺旋形搜潜概率减少；当潜艇初始散布为0.2～0.8 km时，平行航线搜潜概率增加，当潜艇初始散布为0.8～3 km时，平行航线搜潜概率减少；相同条件下，平行航线和扩展矩形搜潜概率明显提高。

图7 4类模型条件下各要素对搜潜概率的影响

4 结论

本文应用直接分析的方法，结合基于关键点飞行线路模拟算法，建立了反潜巡逻机利用磁探仪执行平行航线、扩展矩形和螺旋搜索潜艇的数学模型，仿真分析了相同潜艇运动模型条件下，潜艇初始位置散布、初始距离、潜艇经济航速以及海洋环境磁噪声对磁探仪搜潜概率的影响。结果表明：相同潜艇运动模型条件下，螺旋形搜潜效能最高，且受各要素影响较小；当潜艇进行航向机动时，平行航线与扩展矩形搜潜概率明显提高；当潜艇只进行航速机动时，3种搜潜方法的搜潜概率都明显下降，这对于潜艇规避具有一定的意义。

[1]张海波,杨金成.现代潜艇技术[M].哈尔滨∶哈尔滨工程大学出版社,2002∶186-188.

[2]张阳程,盛飞,王光源,等.航空磁探仪搜索概率模型建立与仿真研究[J].海军航空工程学院学报,2008,23(3)∶332-335.

[3]吴芳,杨日杰,周旭,等.航空磁探仪应召搜潜效能研究[J].测试技术学报,2008,22(2)∶114-117.

[4]韩瑞新,李春洪,陆勤夫,等.航空反潜中的磁探仪系统仿真研究[J].系统仿真学报,2009,21(9)∶2753-2756.

[5]PETER V C,ALEXANDER R P,BRIAN R W,et al.Magnetic detection and tracking of military vehicles[R].Pennsylvania∶Aero Electronic Technology Department of Naval Air Development Center,2002.

[6]HRISTOFOROU E.Magnetic effects in physical sensor design and development[J].Journal of Optoelectronics and Advanced Materials,2004,4(2)∶245-265.

[7]KETTER T N.Anit-submarine warfare in the 21st century[R].Pennsylvania∶Naval Operation Centre,2004.

[8]WALTER L H,PAUL H P.Comparision of aircraft maneuver compensators for antisubmarine warfare magnetometers[R].Pennsylvania∶Naval Air Development Centre,1981.

[9]母攀良,王丹霞,陈凯民.塔台模拟机中基于关键点的线路飞行模拟[J].中国民航飞行学院学报,2007,18(1)∶24-26.

[10]屈也频,廖瑛.潜艇位置散布规律与搜潜效能评估模型研究[J].系统仿真学报,2008,20(12)∶3280-3283.

[11]FORREST R N,EAGLE J N.An empirical analysis of a submarine motion model[R].California∶Naval Postgraduate School,1991.

[12]FORREST R N.Some notes on search,detection and localization modeling[R].California∶Naval Postgraduate School,1983.

[13]海军装备论证中心.国外反潜战[M].北京∶海军出版社,1987∶192-193.

[14]屈也频.反潜巡逻机搜潜辅助决策系统研究[D].长沙∶国防科学技术大学,2009.

[15]SHEINKER A,SALOMONSKI N,GINZBURG B,et al.Network of remote sensors for magnetic detection[C]//International Conference on Automatic Control.USA∶IEEE Press,2006∶56-60.

[16]EDWARD P LOANE.Speed and depth effects in magnetic anomaly detection[R].Pennsylvania∶Naval Operation Centre,1976.

[17]PATRICIA A T.Some priorities for a target probability area[R].Pennsylvania∶Naval Operation Centre,2001.

[18]JAMES A BRONNAN.The influence of the natural environment on MAD operations[R].Pennsylvania∶Naval Operation Centre,1972.