基于FWFPN的装备保障性定性指标评价算法

魏 勇，刘著卿

（海军航空工程学院研究生管理大队，山东 烟台 264001）

0 引言

对武器装备进行保障性定性指标评价的研究有两个积极的意义。一是确定装备保障性要求的满足程度；二是为承制方和部队使用部门提供设计时使用的辅助决策。对承制方和使用部队来说，适时恰当地进行保障性评价是一个重点和难点问题，研究如何适时进行武器系统的保障性评价已成为国内外装备综合保障领域的重要课题，其成果无疑具有重大的军事意义和巨大的经济效益。

保障性评价的技术和方法起始于西方国家。20世纪60～80年代，是综合评价蓬勃兴起的年代。我国从上世纪60年代起开始了系统评价工作的研究，在各行各业都有较多的应用；我军从80年代开始系统评价的研究，并在装备可靠性评价、维修性评价、战场损伤和修复评价（BDAR）、武器系统作战效能评价[1]、备件配置效果评价等进行了系统的研究，得到大量的研究成果[2-3]。

本文在对保障性定性指标分析研究基础上，[4-5]建立了一种基于模糊理论和Petri网理论的加强带权模糊Petri网（FWFPN，Fortified Wighted Fuzzy Petri Net）。在研究FWFPN 基本理论的基础上，建立了FWFPN形式化推理算法，根据舰炮定性指标的特点和指标重要度的分析，对该算法进行了应用及验证。

1 加强带权模糊Petri网定义

1.1 基本模糊Petri网定义

基本的模糊Petri网[6-7]结构为一个8元组形式：FPN=(P,T,I,O,f (t),a (p),D,β)，其中：P是有限的库所集，P=(p1,p2,…,pn)；T是有限变迁集，T=(t1,t2,…,tn)；I为输入函数，即从变迁集到库所集的一个映射；O为输出函数，是从变迁集到库所集的另外一个映射；f:T → [0,1]，是定义在变迁集合T 上的一个取值于[0,1]中实数的函数，表示变迁结点的触发阈值，即变迁到其确定因子的映射；a:P → [0,1]，是定义在库所集合P 上的一个取值于[0,1]中实数的函数，表示库所结点在推理开始时的初始标记状态，即已知命题的可信度，未知命题的可信度定义为0；D表示命题的有限集合，D=(d1,d2,…,dn)，|P|=|D|且P ∩ T ∩ D=∅，任意di∈ D表示一个命题；而 β:P → D为库所与命题之间的对应关系函数。具体的解释如下：O (ti)表示变迁ti的输出库所的集合；I (ti)为ti的所有输入库所的集合；f (ti)=μi表示 ti的确定因子（CF：Certainty Factor）为μi；a (pi)=ai表示 pi的托肯值为ai。如果 β(pi)=di，则表明库所pi与命题 di相对应，即在FPN 中该库所就代表对应的命题，它的托肯值就是相应命题的真值。因此，可以得出结论：如果a (pi)=ai，并且β(pi)=di，则命题 di的真值为ai。

1.2 加强带权模糊Petri网定义

FWFPN是建立在普通的FPN的基础上的，所不同的是通过引入模糊集可信度的概念，赋给FPN中的库所托肯值以及变迁的确定因子以[0,1]上的模糊数，且赋给FPN 中的库所以[0,1]上的模糊权值。所以，FWFPN 比FPN 要多考虑以下问题[5]：

1）前提条件在规则中的权重，它代表每个条件对于结论贡献的大小；

2）规则实现所需的阈值，这是推理得以进行的最低可信度，太低的可信度会使结论失去实际意义；

3）结论的可信度，它代表了条件满足时结论的可信程度。

由此，可以定义：

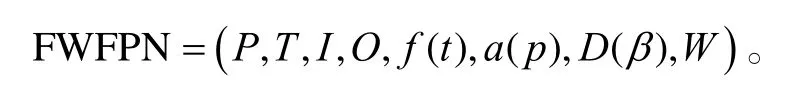
式中：P、T、I、O、f (t)、a (p)的定义与FPN的定义相同；D (β)为如条件成立可推出的结论，β为结论的可信度，D(β)=(d1(β1),d2(β2),…,dn(βn))；W:P → [0,1]上的模糊数，为库所的模糊权值的映射。这样，a (pi)即为pi的模糊托肯值，W (pi)为pi的模糊权值。

2 加强带权模糊Petri网的知识表达

在模糊规则中加上“or（或）”或“and（与）”算符就形成了模糊规则。可以用在条件或结论中，且没有个数的限制。所以，FWFPN的知识表达可以表示为：

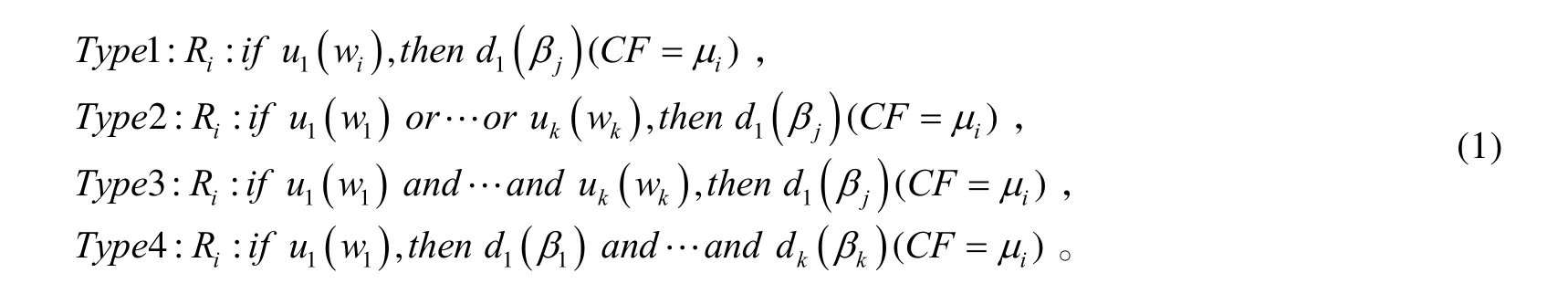
式中：wi(i=1,2,…,n)为前提条件的权系数，权系数满足条件 ∑ wi=1；βj为每个结论的可信度，满足0≤βj≤1(j=1,2,⋅⋅⋅,m)；f为规则可实现的阈值。

3 加强带权模糊Petri网的形式推理算法

在基于模糊产生式规则的知识库系统中执行知识分析、推理、决策支持等相关的推理时，从已知的前提命题的值推导出结果命题的值，相应的推理算法一般都建立在整个知识库系统上[8-10]。因此，有必要建立一个算法，把与问题相关的部分规则从整个知识库系统中分离出来，建立在这一小部分规则集上的知识推理要简单得多，也更容易满足实时性的要求。

本文提出的推理算法建立在矩阵运算的基础上。根据FWFPN的定义，采用矩阵的形式描述如下：

3.1 FWFPN的矩阵形式

1）Δ=(δij)为输入矩阵，δij∈ [0,1]，表示 pi到tj上的输入关系和权重。当pi是tj的输入时，δij等于 pi到tj输入弧上的权系数wi；当pi不是tj的输入时，δij=0，其中：i=1,2,…,n，j=1,2,…,m。

2）Γ=(γij)为输出矩阵，γij∈ [0,1]，表示 tj到pi上的输出关系和结论的可信度；当pi是tj的输出时，γij等于变迁 tj推出结论 pi的可信度 βij；当pi不是tj的输出时，γij=0，i=1,2,…,n，j=1,2,…,m。

3）a=[a1,a2,…,an]T为定义在模糊库所集P 上的状态向量，表示各命题的可信度，ai∈ [0,1]，i=1,2,…,n。a0=[a10,a20,…,an0]T表示命题的初始可信度。

4）f=[f1,f2,…,fm]T为变迁的阈值，fj∈ [0,1]，j=1,2,…,m。

3.2 计算算子

设A、B、C均为n×m维的矩阵[11]，则有以下计算算子：

加法算子⊕：C=A ⊕ B ⇔ Cij=max (aij,bij)；

直乘算子 ⊗：C=A ⊗ B ⇔ cij=aij×bij，i=1,2,…,n，j=1,2,…,m。

3.3 推理算法

设某个推理过程中有n个命题、m个推理规则，表现在FWFPN模型中则有n个库所、m个变迁，FWFPN的输入矩阵 Δn×m、输出矩阵 Γn×m、变迁的阈值向量f和状态矩阵a。其推理过程分解为以下几步进行[12-13]。

步骤1：利用专家评判法求出初始状态矩阵 a0及性能等级评判矩阵V；

步骤2：根据FPN的可信度，求出推理规则的可信度因子CF 作为推理规则变迁f的阈值；

步骤3：根据FWFPN的定义求出其输入矩阵Δ、输出矩阵Γ；

步骤4：计算经过第1 轮推理后模糊输出库所的状态为

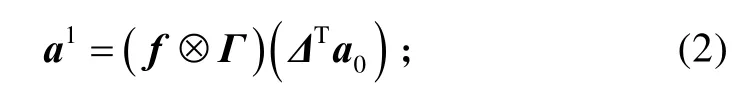
步骤5：计算当前经过第1 轮推理后，可得到的所有命题的状态

步骤6：用上式中的a1代替式(2)中的a0，反复用式(2)～(3)进行迭代，设ak为第k步推理得到的结论，则在第k步推理进行后，所有命题的状态为：ak=ak−1⊕ak；

步骤7：当推理计算不再使任何命题的状态发生变化时，即 ak=ak−1时，推理结束。

将上述推导过程归纳为一个算式，可得：

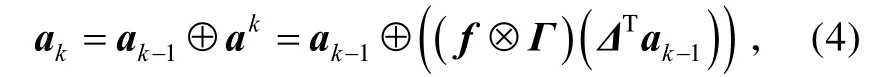
4 实例分析

基于上述思想，FWFPN 应用了模糊集理论、决策理论、集合理论等中的概念，充分考虑了评价指标的特征，因而可建立基于FWFPN的定性指标评价模型。舰炮装备的定性指标体系是一个多级的评价体系，分为目标层、子目标层、准则层、子准则层、指标层、一级子指标和二级子指标。为了便于描述，这里只给出两级评价指标的评价建模思路。假定有一个简单的两级指标，目标层和指标层。假定底层指标有n个指标 U=(u1,u2,…,un)，与之对应的目标层为Y。则基于FWFPN的评价模型如下。

4.1 指标体系的建立及权重的计算

以舰炮装备的保障系统与保障资源的定性指标为例，建立保障性评价指标体系，如图1所示。评价组成员由5位相关专业的专家组成，包括舰炮主设计者、保障性专业教授、研究所工程师、试验厂区高工及岗位使用人员。分别对舰炮装备保障性定性指标的底层指标进行评判打分，评判打分采用评分表的形式。该评分表是在参照相关国军标标准的基础上，结合舰炮装备的实际情况制定的。

权重的计算是根据专家调查法，采用指标主观权重与客观权重相结合的方法计算得到。

图1 定性指标体系组成

4.2 FWFPN 推理规则的建立

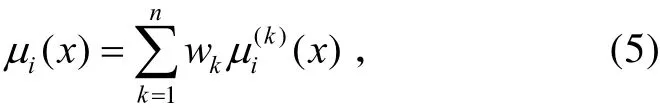
式中：μi(x)为指标x 属于评语 Vi的隶属函数；wk指第k位专家的权重；指第k位专家给出的指标x 属于评语Vi的确信度。按隶属度最大原则，可选指标的隶属度作为库所P的初始可信度0a。

推理规则如下：

规则1：If T211(0.3011) and T212 (0.3953) and T213(0.3036)，Then T21(0.8) (f1(0.2))；

规则2：If T221(0.2548) and T222 (0.5957) and T223(0.1495)，Then T22(0.8) (f2(0.2))；

规则3：If T21(0.5) and T22 (0.5)，Then T2(0.6)(f3(0.2))。

其中：T211表示人员个体素质为优（初始可信度为0.7682）；T212表示人员技术等级为优（初始可信度为0.422）；T213表示人员专业类型为优（初始可信度为0.627）；T221表示器材质量状况为中（初始可信度为0.627）；T222表示器材储备的合理性为中（初始可信度为0.422）；T223表示器材保障是否满足使用和维修的需要状况为差（初始可信度为0.578）；T21表示人力资源保障；T22表示器材保障；T2表示保障系统与保障资源。规则中条件命题后括号中的数字为命题在该规则中的权系数；1f、f2为各规则的阈值，即规则可信度，假设为0.2；结论命题后为结论的可信度，假设为0.8、0.8、0.6。

4.3 评价指标的FWFPN模型

将系统中各事件转化为FWFPN的要素，形成如图2所示的递阶层次结构，即定性指标评价系统的加强带权模糊Petri网模型。

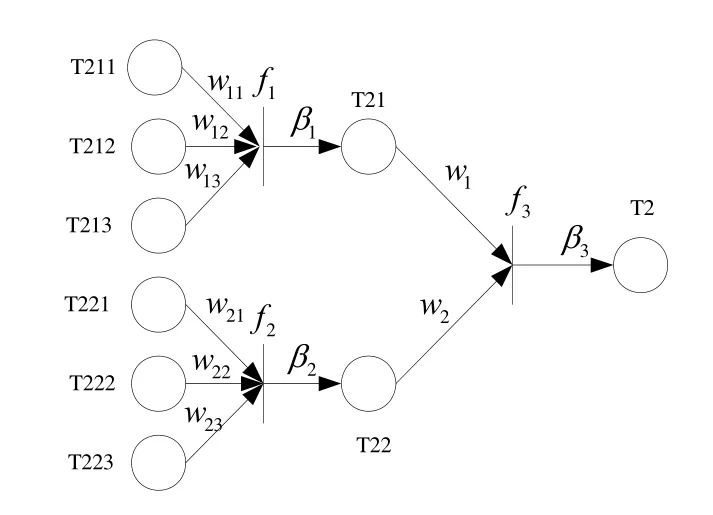
图2 定性指标的FWFPN模型

根据第3节定义1，可得它的矩阵形式：

上算法涉及到大量的矩阵运算，利用MATLAB 语言依据定义3给出的推理算法步骤可容易予以实现，最终结果如下：

由于2、3次迭代的结果相同，所以推理结束。最终的结果如下：

从结果可以看出，人力资源保障为中；器材保障为一般的概率为差；保障系统与保障资源为劣。分析结果原因，主要是在确定权重时，只考虑了专家的主观权重，而没有考虑专家的客观权重。在实际决策过程中，专家所作判断的可信度并不一定与他的主观权重相一致，即使是同一位专家，在判断不同的决策中，其可信度也是不同的。而且，在一般群决策过程中，基本上可以认为邀请的专家具有相同的重要性，即专家具有相同的主观权重。为了全面反映各决策者在群决策过程中的作用，还必须根据具体的群决策问题及群决策方法来确定决策者所作决策的可信度，这种可信度由决策结果及其相互关系所决定，它也应作为决定决策者权重的一部分，称之为决策者的客观权重。这也是今后将继续研究的方向和内容。

5 结论

由于武器装备的保障性定性指标评价信息的不确定性、模糊性，一直以来是军内武器装备保障领域专家、学者十分热衷的课题。因此，产生了多种应用广泛的综合评价方法，如：层次分析法（AHP）、模糊综合评价法等。本文在前人研究的基础上，给出了一种新的可用于装备保障性定性指标评价的算法——基于FWFPN形式推理算法。在研究中，考虑了推理过程中的一些约束条件，包括命题的权重、规则可信度以及结论可信度等条件。并根据专家的评判，对舰炮保障系统与保障资源的两个定性指标进行推理分析和评价，评价结果证实了该方法是可行的。但这种方法还有一些需要说明：

1）权重的计算只考虑了专家的主观权重，而没有考虑专家的客观权重。

2）文中规则可信度的确定是由相关领域专家给出的情况下参与计算的。因此，在较大程度上存在着主观和人为的因素。实际上，针对定性指标信息的不确定性和模糊性，采用粗糙隶属度函数方法来确定规则的可信度因子，将定性指标的模糊隶属度引入到粗糙隶属度函数中，可减少可信度因子的主观因素,增加理性和客观的成分，有效提高应用可信度理论进行不确定性推理的可靠性。

3）文中结论可信度的确定是由相关领域专家给出的情况下参与计算的，存在着主观和人为的因素。实际在可信度理论中，采用产生式规则IF A THEN B with CF(B,A)来描述一条知识，若 A (d)=α，则由模糊产生式推理规则IF A THEN B with CF，得B在对象 d 上的可能性 B (d)。即 B (d)是A (d)与CF(B,A)的函数，记为R，B (d)=R (A (d),α)，很明显 B (d)既依赖于模糊集A的隶属度 A (d)，又依赖于推理规则的可信度CF(B,A)。

[1]王涛,端木京顺,王晓钧.基于模糊综合评价DEA方法的信息化部队作战能力评估[J].军事运筹与系统工程,2006,20(3):69-72.

[2]庄则平.船舶安全检查处理决策的定量评价研究[D].大连:大连海事大学,2001.

[3]贺挺.大型商场建筑消防安全评估[D].重庆:重庆大学,2005.

[4]徐宗昌,黄益嘉,杨家伟.装备保障性工程与管理[M].北京:国防工业出版社,2006.

[5]曹小平,孟辉,周红,等.保障性论证[M].北京:海潮出版社,2005.

[6]鲍培明.模糊Perti网模型的反向推理算法[J].南京师范大学学报:工程技术版,2003,3(3):21-25.

[7]贾立新,薛钧义,茹峰.采用模糊Petri网的形式化推理算法及其应用[J].西安交通大学学报,2003,37(12):1263-1266.

[8]CHEN SHYI-MING,KE JYH-SHENG,CHANG JIN-FU.Knowledge representation using fuzzy petri nets[J].IEEE Transactions on Knowledge and Data Engineering,1990,2(3):311-319.

[9]KORIEM S M.A fuzzy Petri net tool for modeling and verification of knowledge-based systems[J].The Computer Journal,2000,43(3):206-223.

[10]FAY A.A fuzzy knowledge-based system for railway traffic control[J].Engineering Applications of Artificial Intelligence,2000,13:719-729.

[11]汤新民,钟诗胜.基于元模型的模糊Petri网反向传播学习算法[J].系统仿真学报,2007,19(14):3163-3166.

[12]LOONEY C G.Fuzzy Petri nets for rule-based decision making[J].IEEE Trans.Syst.,Man,Cybern,1988,18(1):178-183.

[13]CHEN S M,KE J S,CHANG J F.Knowledge representation using fuzzy Petri nets[J].IEEE Trans Knowledge and Data Engineering,1990,2(3):311-319.