噪声干扰环境下基于实测数据的多目标航迹起始算法

张翔宇，李世忠，苏 伟，王国宏

（1.海军航空工程学院电子信息工程系，山东 烟台 264001；2.92619部队，广东 深圳 518000）

0 引言

随着科学技术的发展，如何更快更好地对目标进行跟踪拦截，进而取得战场上的主动权是当今世界研究的热点和难点。而航迹起始作为跟踪的第一步，能否实现航迹的快速起始显然是能否实现快速跟踪的重要因素。但是在航迹起始时，目标距离雷达一般较远，传感器探测分辨力低、测量精度差，加之真假目标混杂未知，因而多目标航迹起始问题就显得非常复杂。

现有的起始算法有直观法[1]、逻辑法[2]和Hough变换法[3-4]等基本算法。在这里，直观法计算简单，但它是一种确定性较为粗糙的算法；Hough变换法确定性虽强，却需要多次扫描才能较好地对目标进行起始；而逻辑法不仅算法简单，且便于实现，因而在工程领域已被广泛应用。而依据文献[1-6]，在无干扰环境下，3/4逻辑法的起始效果最好，但在干扰环境下，逻辑法和修正逻辑法的起始效果如何却有待进一步研究。

因此，本文在文献[6-12]的基础上，就干扰环境下的起始问题进行了深入研究，并借助该环境下的实测数据对其做出了进一步的比较验证，以求得出一些对工程实践有意义的结论。

1 逻辑法和修正逻辑法简介

1.1 逻辑法

在无干扰环境下，3/4逻辑法是最为合适的算法，但是在干扰环境下，由于传感器量测的不确定性，该方法往往会产生大量虚假目标，进而给后续的工作带来极大困扰。相比而言，5/5逻辑法通过提高逻辑却能较好地消除虚假航迹和对目标进行起始。因此，本文将以5/5逻辑法为例来对逻辑法做简要介绍，并在实测验证中将其与3/4逻辑做进一步比较验证。其具体工作方式如图1所示。

图1 工作方式图

1)假定在x，y坐标系中，以暂时航迹的第一个点 p1[zx(1),zy(1)]为圆心，vmaxt、vmint分别为半径构成圆环形区域。如果下一个周期雷达在此区域内观测到新的点迹，则暂时航迹形成了第二个点 p2[zx(2),zy(2)]，否则将删除该暂时航迹。对应的关联域1可由下式确定：

式(1)中：vmax、vmin分别为目标运动的最大速度和最小速度；t为雷达的扫描周期。

2)在获得p1[zx(1),zy(1)]、p2[zx(2),zy(2)]点后，可将该两点连成一条可能航迹，并对其按式(2)进行直线外推，以得到点。

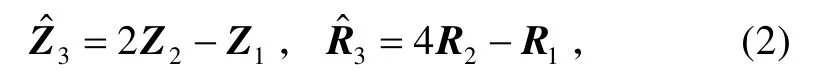
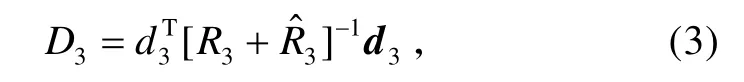
式中，

这里 D3是服从自由度为p的χ2分布的随机变量。由给定的门限概率查表可得门限γ，若第3次扫描量测所得的最小D3min值小于γ，则对该D3min值所对应的量测点 p3[zx(3),zy(3)]给予互联(此时量测点p3[zx(3),zy(3)]到外推点的距离最近)。

4)在第4次和第5次扫描中重复步骤3)，以得到相应的关联点 p4[zx(4),zy(4)]和p5[zx(5),zy(5)]，从而形成稳定航迹，这时航迹起始方算完成。

5)在历次扫描中，均未落入相关波门参与数据互联判别的那些量测均作为新的航迹头，转步骤1)。

1.2 修正逻辑法

相对逻辑法而言，修正的逻辑法在虚警概率较高的情况下可快速的对目标进行起始，并且两者的计算量处于同一数量级，因而在工程应用中具有很大的实用价值。其主要思想是在航迹起始阶段，对落入相关波门中的量测添加一个角度修正和加速度修正的限制。

1.2.1 角度修正

在航迹起始时，目标相对雷达的距离较远，一般在做匀速运动或匀加速直线运动。这时“V”字形的量测点迹明显有悖于常理，进而本文通过角度修正的方式将其予以剔除。如图2所示。

图2 角度修正图

令ϕ为矢量 Zi+1−Zi和Zi−Zi−1之间的夹角，即：

1.2.2 加速度修正

在航迹起始时，初始协方差一般较大，往往会使后续外推的波门偏大，进而导致相邻两个互联点间的距离随之加大，最终与常理相悖(这里本文称之为“一”字形偏差)，如图3所示。

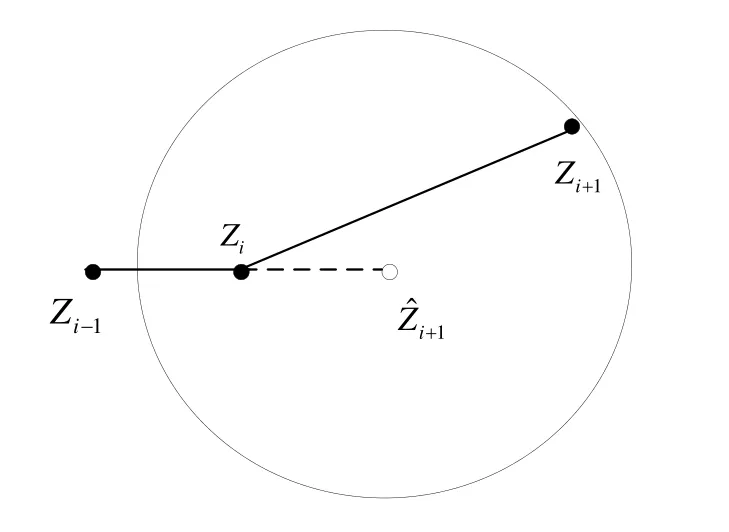
图3 距离偏差图

于是本文借助加速度修正的思想，通过使所测加速度的绝对值小于最大加速度 amax来进一步剔除“一”字形误差。即：

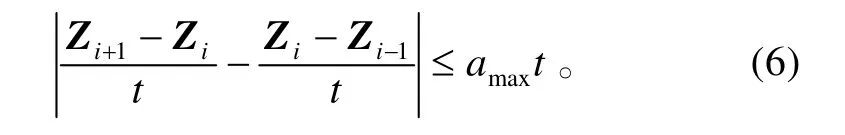
通过这一条件可以有效地剔除干扰，稳定航迹。

2 基于实测数据分析

航迹起始时，目标相对雷达的距离一般较远，其运动往往可看作匀速运动或匀加速直线运动，而该特性恰好与民航飞机的对应特性相符，于是本次试验将借助某地民航飞机的实测数据来进一步验证该算法的可靠性。

2.1 试验条件

1)监视范围：x ∈[−5 00km,500km]、y ∈[−5 00km,500km]的正方形区域。

2)工作条件：11:35雷达开机，11:40 干扰机开机，双频干扰。两种条件下所对应的量测点迹分别如图4、5所示。

3)采样间隔：t=10 s。

4)运动方式：近似的匀速运动和匀加速直线运动。

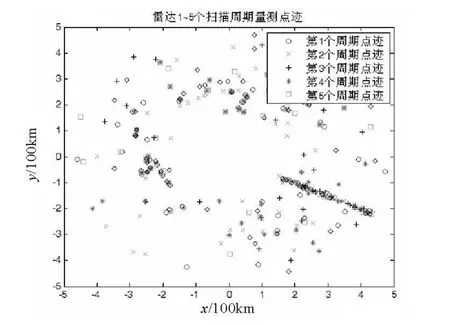
图4 无干扰环境下的量测点迹图

图5 干扰环境下的量测点迹图

2.2 验证结果

2.2.1 无干扰情况

在图4所示的无干扰环境下，分别用3/4逻辑法和5/5逻辑法对目标的量测点迹进行起始，得到的相应起始航迹分别如图6a)和7 a)所示。由于目标间的距离一般较大，在图中往往不易观察，于是将其对应部分放大后分别如图6b)、6 c)和图7b)、7 c)所示。

图6 3/4逻辑法所对应的起始航迹

图7 5/5逻辑法所对应的起始航迹

2.2.2 干扰情况

1)在图5所示的干扰环境下，分别用3/4逻辑法和5/5逻辑法对目标的量测点迹进行起始，得到的相应起始航迹分别如图8～9所示(目标相距较大的问题在上节中已做详细介绍，这里就不做过多说明)。

2)采用逻辑法对目标进行航迹起始不可避免的会产生所谓的“V”字形误差(图9左上部分，将其放大后得图10)和“一”字形误差(见图9右上部分)。此时，分别在5/5逻辑法的基础上添加角度修正和加速度修正，可消除相应的“V”字形误差和“一”字形误差，见图11～12，将两者相结合，效果见图13。

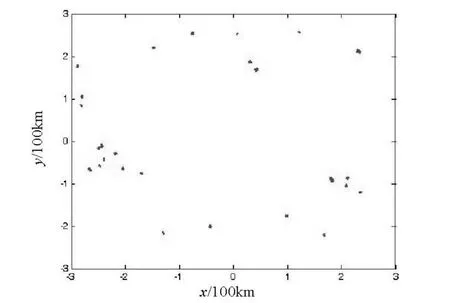
图8 3/4逻辑法所对应的起始航迹

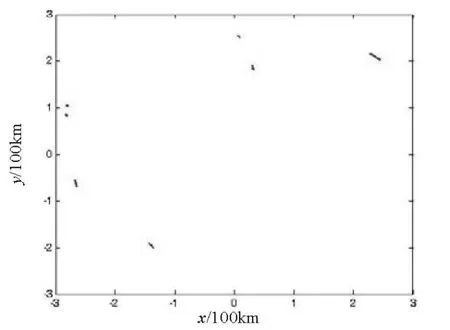
图9 5/5逻辑法所对应的起始航迹

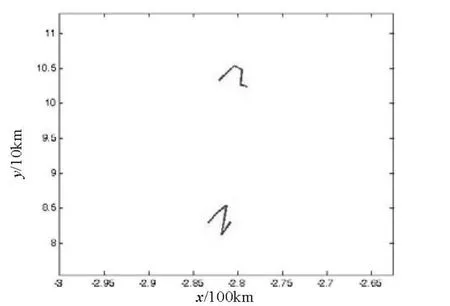
图10 “V”字形误差图

图11 角度修正后所对应的起始航迹

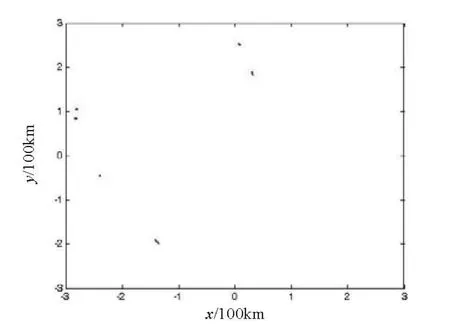
图12 加速度修正后所对应的起始航迹

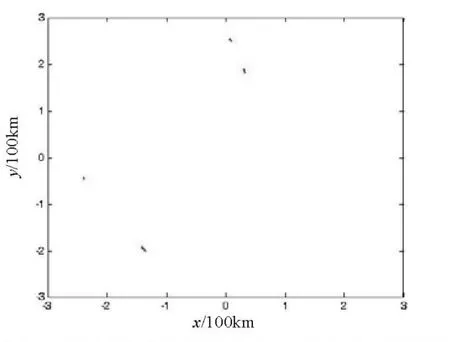
图13 修正的5/5逻辑法所对应的起始航迹

2.3 结果分析

分析图6～13，可得到以下几点结论：

1)将图6和图7进行比较可得，在无干扰环境下，3/4逻辑法和5/5逻辑法起始的效果都很好，两者差别不是很大；

2)由图8可得，在干扰环境下，3/4逻辑法起始混乱，虚假目标较多，不利于后续工作的继续进行；

3)将图8和图9进行比较可得，在干扰环境下，5/5逻辑法起始效果良好，虚假目标较少，效果明显强于3/4逻辑法；

4)将图11～13分别与图9进行比较可得，修正的5/5逻辑法在5/5逻辑法的基础上可对应消除起始中所谓的“V”字形误差和“一”字形误差，起始效果相对前者更好，便于后续工作的继续进行；

5)将图13和图7进行比较可得，在干扰环境下，修正的5/5逻辑法起始的航迹近似于无干扰情况，起始效果很好，便于工程实践；

综上所述，在干扰环境下，m/n逻辑法当滑窗中的检测数m和相继事件数n都较大时起始效果较好；修正逻辑法在前者的基础上加入限制条件后起始效果会更好。

3 结束语

本文就干扰环境下的起始问题进行了深入研究，对逻辑法和修正逻辑法做出了重点介绍，并通过相应的实测数据对其完成了对比性验证。验证结果表明，在干扰环境下，该算法可较好地实现多目标航迹的起始。

[1]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].北京:电子工业出版社,2006:83-89.

[2]袁刚,苏峰.基于目标运动特性的逻辑航迹起始方法[J].舰船电子工程,2010,30(5):81-83.

[3]孟藏珍,闫抒升,王晓军,等.密集杂波环境下的多目标航迹起始算法研究[J].舰船电子对抗,2009,32(1):72-76.

[4]苏峰,魏广芬,魏志轩.三维空间中基于修正逻辑的快速航迹起始算法[J].系统仿真学报,2008,20(6):1420-1422.

[5]汤琪,黄建国,杨旭东.航迹起始算法及性能仿真[J].系统仿真学报,2007,19(1):149-152.

[6]陈小伟,林家骏,张洁.修正的逻辑航迹起始算法性能研究[J].华东理工大学学报,2006,32(5):1346-1350.

[7]苏峰,王国宏,何友,等.修正的逻辑航迹起始算法[J].现代防御技术,2004,32(5):66-68.

[8]朱洪艳,韩崇昭,韩红,等.航迹起始算法研究[J].航空学报,2004,25(3):284-288.

[9]罗鹏飞,张文明.一种多目标跟踪航迹起始新算法及其性能评估[J].国防科技大学学报,1999,21(6):51-54.

[10]GUO R J,ZONG C G,YUAN Y S,et al.Track initiator for multiple-target tracking in polar coordinates based on modified hough transform[C]//International Symposium on Instrumentation Science and Technology.2004:1053-1058.

[11]KIRIL M.Multiple target tracking using hough transform PMHT algorithm[C]//2002 First International IEEE Symposium “Intelligent Systems”.2002:227-232.

[12]LEUNG H,HU Z,BLANCHETTE M.Evaluation of multiple target track initiation techniques in real radar tracking environments[J].IEEE Proc.Radar,Sonar Navig.1996,143(4):23-28.