空气静压电主轴过盈联接研究
贾月明,王明权,李战伟
(1.北京中电科电子装备有限公司,北京 100176;2.中国电子科技集团公司第四十五研究所,北京 101601)
空气静压电主轴是切割机、减薄机等精密加工设备的核心功能部件,其性能直接影响设备的加工品质。空气静压电主轴采用空气轴承支撑,变频电机无级调速,具有转速高、旋转精度高、稳定性好、摩擦小、容易散热等优点。为实现高转速高可靠性强力磨削,主轴必须具有优良的运转精度和转矩传递能力,其零部件应具有良好的加工精度、表面质量和装配精度。为了保证达到严格要求的G0.4级动平衡精度,转轴与电机转子之间采用无键过盈联接,实现了主轴系统的零传动[1]。过盈量的大小直接影响空气静压电主轴的性能。过盈量偏大会增加主轴装配难度,降低装配精度,甚至毁坏精密零件;过盈量偏小则会影响主轴旋转精度和转矩传递能力。因此,有必要研究转轴与电机转子之间的过盈联接,科学合理地选择过盈量,计算并校核零件强度,分析过盈联接表面的应力分布。
1 主轴过盈联接理论计算
转轴与电机转子之间过盈联接时,在配合表面处会产生一定的正压力,引起转轴内外径压缩,电机转子内外径扩张[2]。一般地,转轴和电机转子的轴向长度较大,其轴向伸长量可以忽略。因此,转轴和电机转子的配合可以简化为两个厚壁圆柱套筒的过盈联接。转轴与电机转子之间的过盈量的确定,既要满足静态转矩传递能力的要求,又要满足主轴高速旋转的动态要求。
1.1 主轴静态过盈量计算
转轴与电机转子均采用钢质材料,其弹性模量和泊松比基本相等[3]。在静态配合条件下,转轴与电机转子之间的静态过盈量,可由下式确定:

式中:kc为安全因子,一般取2~4;v为转轴与电机转子材料的泊松比:Mt为主轴的传动转矩;μ为转轴与电机转子配合表面间的摩擦系数;E为转轴与电机转子材料的弹性模量;B为转轴与电机转子配合面的有效接触长度;a为电机转子的内孔半径;b为电机转子的外圆半径;c为转轴的内孔半径;ce为电机转子的内外径比ce=a/b;ci为转轴的内外径比,ci=c/a。
1.2 主轴动态过盈量计算
主轴高速旋转时,必须考虑离心力对过盈量的影响。在高速运转条件下,转轴与电机转子之间的动态过盈量,可由下式确定:

式中:ρ为电机转子材料的密度;ω为电机转子的角速度。
由式(1)和式(2)可知,静态过盈量与主轴的转矩传递能力有关,与主轴传递的转矩成正比;动态过盈量则主要由离心力确定,与主轴转速的平方成正比。转轴与电机转子之间的最小过盈量等于静态过盈量与动态过盈量之和。
1.3 主轴过盈联接计算
某型号空气静压电主轴,转轴的外径2a=45mm,转轴的内径2c=20mm;电机转子的外径2b=70mm,电机转子的内径2a=45mm,电机转子的轴向长度L=32mm,电机转子过盈联接表面的有效接触长度B=30mm;主轴最高转速ω=20000 r/min,额定功率P=6 kW,额定转矩Mt=9.55 N·m。转轴和电机转子均采用钢质材料,其弹性模量 E=2.06×1011N/m2,泊松比 v=0.3,转轴与电机转子配合面间的摩擦系数μ=0.1,转轴材料的许用应力[σ1]=6.35×108N/m2,电机转子衬套材料的许用应力[σ2]=2.87×108N/m2。
根据式(1),转轴与电机转子间的静态过盈量△s=0.00217mm
根据式(2),转轴与电机转子间的动态过盈量△d=0.00664mm
由上述计算可知,空气静压电主轴要求的动态过盈量△d是其要求的静态过盈量△s的3倍多。转轴与电机转子之间过盈联接的最小过盈量△min=△s+△d=0.00881mm。
在该型号电主轴设计时,转轴与电机转子的配合采用覫45H6/r5,该配合最小过盈量0.018mm>0.00881mm,因此过盈联接能够满足电主轴高速旋转时的转矩传递要求。该配合最大过盈量0.045mm,过盈联接表面产生的最大正应力为:

电机转子内孔表面具有最大的切向拉应力σθemax和最大的径向压应力 σremax,其值分别为:


转轴的配合面上具有最大的径向压应力σrimax,转轴内孔表面具有最大的切向压应力σθimax,其值分别为:

由上述计算可知,电主轴的危险点处于电机转子的内表面,根据第三强度理论[4]:
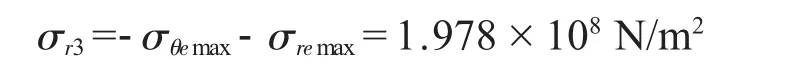
电机转子衬套材料的许用应力 [σ2]=2.87×108N/m2>σr3,说明转轴与电机转子之间的过盈联接是安全可靠的。
2 主轴过盈联接有限元分析
主轴过盈联接表面产生的应力,无法采用传统的测量方式进行观察。从力学角度来讲,主轴过盈联接是一种非线性接触行为,可以利用非线性有限元分析方法求解其接触应力。利用ANSYS软件,可以对主轴过盈联接采用动态接触计算方法仿真其压装过程。
2.1 转轴与电机转子有限元模型的建立及网格划分
转轴与电机转子的结构示意图如图1所示。
由于结构和载荷的对称性,采用轴对称分析模型,取轴向的一半进行建模,在不影响计算精度的情况下可以减少计算量和节约磁盘空间,建立的有限元模型如图2所示。

图1 转轴与电机转子过盈联接的结构示意图

图2 过盈联接有限元模型
设置材料的性能参数后,采用PLANE182单元进行网格划分。
2.2 生成接触对并求解
在转轴与电机转子过盈联接表面设置接触单元时,选取Targe169来模拟“目标”面上的接触单元,用Conta172来模拟“接触”面上的接触单元,生成2D接触对。
在求解器中,完成非线性分析设置,施加位移边界条件等。
2.3 模拟结果
动态压装过程中某一时刻,主轴过盈联接的应力分布如图3所示;动态压装过程结束后,主轴过盈联接的应力分布如图4所示。

图3 主轴压装过程中过盈联接的应力分布

图4 主轴压装结束后过盈联接的应力分布
从图4中可以看出,最大应力发生在电机转子的内表面处,其值为,与理论计算的最大应力值十分接近,能够满足空气静压电主轴高速旋转时的转矩传递要求。
3 结 论
合理选择转轴与电机转子之间的过盈量,是空气静压电主轴过盈联接设计的基本工作。本文采用解析法计算了过盈量,进行了过盈联接应力分析和强度校核;并利用有限元分析软件ANSYS模拟了主轴动态压装过程的应力分布。经过对比,有限元分析结果与理论计算非常接近,能够较好地满足空气静压电主轴的工作要求。本文对空气静压电主轴过盈联接的研究方法,对于类似产品的设计,具有一定的借鉴和参考意义。
[1]刘素华,袁世先.电主轴关键技术及工艺要点[J].安阳师范大学学报,2003(5):71-73.
[2]马平,张伯霖,李锻能,等.高速机床电主轴过盈配合量计算[J].组合机床与自动化加工技术,1999,18(3):12-14.
[3]成大先.机械设计手册(第1卷)[M].北京:化学工业出版社,2002.
[4]章梓茂.材料力学[M].北京:高等教育出版社,2005.
[5]段进,倪栋,王国业.ANSYS10.0结构分析从入门到精通[M].北京:兵器工业出版社,2006.

