音频信号的混沌特性分析

鲍 枫 ,刘 鑫 ,贾懋 ,鲍长春

(北京工业大学电子信息与控制工程学院语音与音频信号处理研究室,北京 100124)

1 引 言

近年来,非线性研究得到了快速发展,已广泛应用到天文、水文、气象以及经济领域。通过对事物已知的时间序列进行非线性分析来预测其未来的演变趋势是非线性研究的核心所在。随着科学技术的发展,在许多学科之中都出现了非线性问题。传统的线性化方法已不能满足解决非线性问题的要求,非线性动力学也就由此产生。非线性动力学中的相空间重构理论对音频频谱非线性特性的分析有着巨大的吸引力。目前,在语音与音频信号的非线性分析方面,已有科研人员对语音序列进行了非线性分析[1,2],而针对不同类型音频信号频谱信息非线性特性的统计分析还有待进一步研究[3-5]。基于该背景,本课题针对各类型音频信号的修正离散余弦变换(Modified Discrete Cosine Transform,MDCT)系数的混沌特性展开分析和研究。

相关文献证明,最大李雅普诺夫(Lyapunov)指数定量地表征了相空间中两相邻轨线运动的发散情况,当某一序列的最大Lyapunov指数为正时,可以判定该段信号存在混沌现象[4-8]。基于此,本课题通过对MDCT域序列的最大Lyapunov指数进行统计分析,来验证音频信号频域信息的非线性特性,最终实现一种基于最大Lyapunov指数的音频信号MDCT系数混沌特性分析方法,为非线性动力学理论引入音频信号处理领域奠定基础。

2 MDCT变换

MDCT是音频编码中常用的一种变换编码技术,其原理是:将原来在时间域相关性很强的信号,经正交变换,转化为在变换域内的一组系数,通过对变换域基矢量的选择,大大减弱变换域系数之间的相关性,并使得信号能量主要集中在某些系数上,从而达到对数据压缩的目的。由于采用了时域混叠消除技术,因此与传统DCT变换相比,MDCT可以有效地减小变换域系数量化失真所造成的边界效应。

MDCT可以定义为

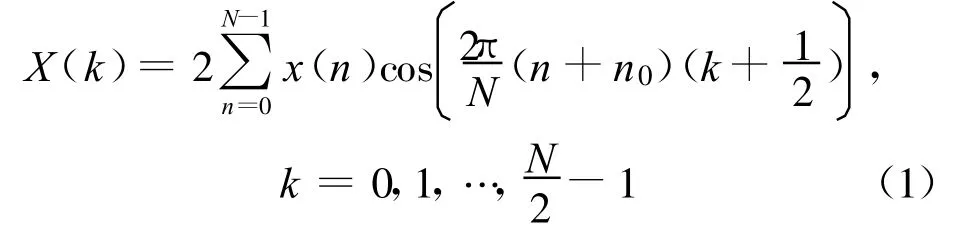
式中,x(n)(n=0,1,…,N-1)表示长度为N的时域信号。为消除边界块效应,引入时域混叠消除技术对信号进行加窗处理,窗函数选择正弦窗,即:

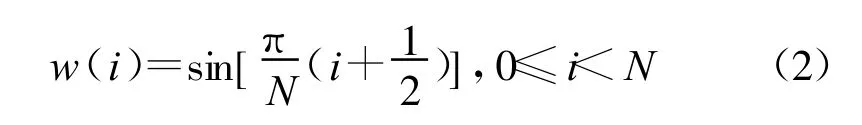
加窗后MDCT定义为

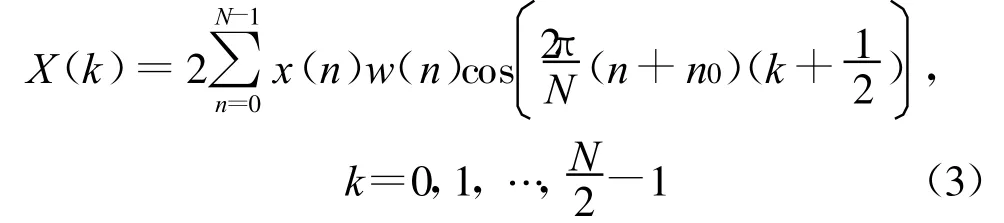
由于采用了时域混叠消除技术,时域信号在进行时频分析时将采用50%的叠接方式进行逐帧MDCT。

由于MDCT具有良好的正交性、稀疏性以及消除块效应的能力,本文采用MDCT作为音频信号时频分析的主要工具,从而为其频域信息非线性特性的分析奠定基础。

3 相空间重构

对于一个混沌系统来说,经过一段时间变化,其产生的运动轨迹会呈现出一定规律。而由于观测条件的限制,通常只能通过某些实验观测方式来获得表征动力学系统特性的一组时域序列。系统中任意分量的形成都是由其与之相关联的分量所共同决定,这样可以从某一分量中提取并重构出系统的相空间,从而恢复出原来动力学系统所表征的运动规律,这种方式称作相空间重构技术。非线性动力学则是在重构相空间的基础上对复杂系统运动规律展开研究的。在相空间重构过程中,通常采用时间延迟法。该方法选取适当的延迟时间,取整数倍延迟后的观测值作为新的坐标,从而构成一个多维状态空间。可以证明这样的空间可以将原始混沌系统中吸引子的许多特性保存下来,同时初步确定该系统真实相空间的维数[6]。

在相空间重构过程中最重要的两个参数分别为延迟时间 τ和嵌入维数m。由F.Takens的延迟嵌入定理可知[8],在时间序列无限长、无噪声、无限精确的情况下,可以任意选取τ,但实际测量得到的时间序列是有限长的,且有一定的噪声污染和测量误差,所以只能根据经验来选取延迟时间 τ,同时要使Xn与Xn+τ具有某种程度的独立但又不完全无关。如果τ太小,Xn与Xn+τ的值过分靠近,以至于不能区别它们,相空间轨迹会集中在同一位置,信息被挤压产生大量冗余;如果 τ太大,会导致Xn与Xn+τ不相关,吸引子的轨迹会投影在完全不相关的方向上,不能真实地刻画出轨迹的规律。

序列{Xi}在时间间隔 τ下的自相关函数可以表示为

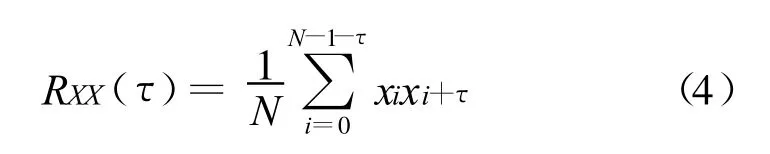
当自相关函数降低到RXX(0)的1-1/e时,可以表明相邻τ点延迟数据之间存在的相关性较低,而系统信息不会过多的丢失,此时的 τ即为重构相空间的时间延迟。

在相空间重构过程中同时还要考虑参数嵌入维数m,同时要满足Takens嵌入定理,即如果嵌入维数m≥2d+1,该条件是充分的,但并不是必要的,其中d为动力学系统的真实维数。如果嵌入维数m过大,虽然相轨迹可以完全展开,但会增加轨迹的计算量。本文采用虚假近邻点法来选择合适的嵌入维数m。随着嵌入维数m的增加,相轨迹逐渐展开,由轨迹折叠产生的虚假近邻点也将逐步剔除。当虚假近邻点数不随维数增加而减少时,证明相轨迹已经完全展开,则将此时的空间维数定义为嵌入维数m。

在m维相空间中,每个相点为X(t)={x(t),x(t+τ),…,x[t+(m-1)τ]},都存在某个距离内最近邻点XN,其距离为Dm(t)=‖X(t)-XN(t)‖。从相空间的维数m增加到m+1维时,这两个相点的距离会发生变化,即:

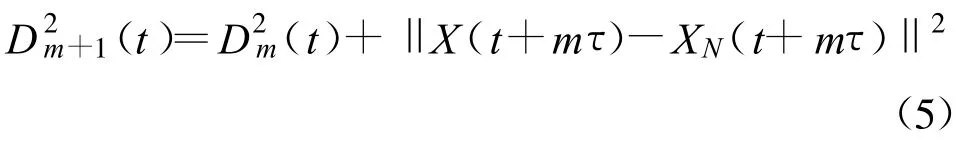
若相点与其近邻点之间的距离有较大变化,则可以认为是由高维奇异吸引子中两个相邻的点在投影到低维相空间上所造成的,此时该近邻点记为伪最近邻点。令Ym表示该距离的相对变化程度,即:

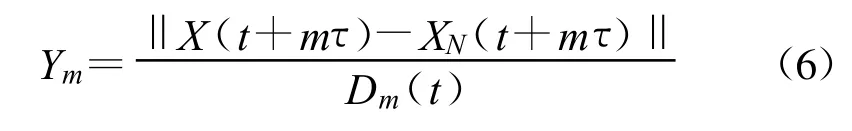
则若Ym>YT,XN可记为虚假最近邻点。阈值YT可在[10,50]之间选取。

在实际测量中,从嵌入维数的最小值开始计算虚假紧邻点的比值,当增加嵌入维数m到伪近邻点的比值小于5%或者伪最近邻点不再随着嵌入维数m的增加而减少时,这时认为相空间完全展开,此时的m为最佳嵌入维数[7]。

通过以上方法对信号进行分析,可以确定其延迟时间 τ和嵌入维数m。利用这两个参数,可以将一维观测序列转换到重构相空间中,构成相应的相点 X(t)={x(t),x(t+τ),…,x[t+(m-1)τ]}。

4 Lyapunov指数

根据非线性动力学原理可知,混沌系统对初始条件具有较强的敏感性。相空间初始距离很近的两条轨迹会以指数速率发散,Lyapunov指数就是根据相轨迹的发散率来定量地判断系统的混沌特性从而初步度量了复杂系统的预测性[7]。

对一维映射y(t+1)=F[y(t)],假设初始位置 y(t0)附近有一点 y(t0)+βx(t0),则经过 n次迭代后,有:

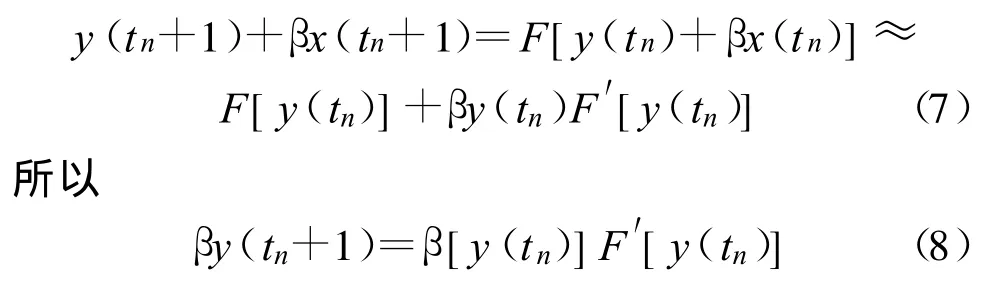
式中,t0、tn分别为预选的初始时间与当前时间。

设相轨迹上两点之间的初始距离为 βx(t0) ,用 βx(tn) 表示经过 n次迭代后该两点之间的距离 ,由式(8),有:

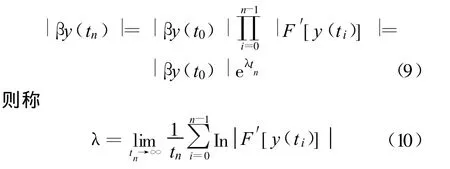
当λ>0,相邻轨迹按指数发散,具有系统混沌特性;λ=0,系统具有周期性;λ<0,系统有稳定的不动点,不具有混沌特性。

本文采用基于Rosenstein小数据量法[7]对Lyapunov指数进行计算,对于一个音频信号时间序列{x(i),i=1,2…,N}进行MDCT变换,利用前一节介绍的相关方法获得延迟时间 τ和嵌入维数m,进而实现相空间重构,重构的相点记为X(t)={x(t),x(t+τ),…,x[t+(m-1)τ]},t=1,2,…,M,其中M=N-(m-1)τ。在相空间中,寻找任意点X(t)的最近邻点 X(t′),即 :

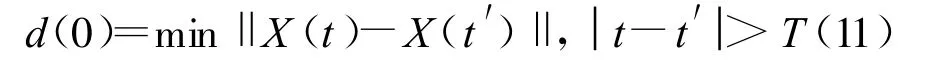
式中,t′=1,2,…,M,且 t≠t′,T为时间序列平均周期,d(0)代表初始时刻一对最近邻点之间的距离。

对于相空间中的每一个X(t),计算出该点与其近邻点在i时刻后的距离d(i):

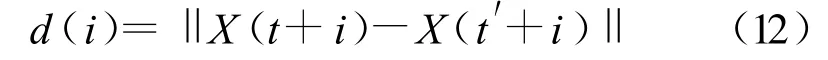
式中,i=1,2,…,min(M-t,M-t′)。对每个时刻i,求出所有相点与其近邻点的平均对数距离,即:

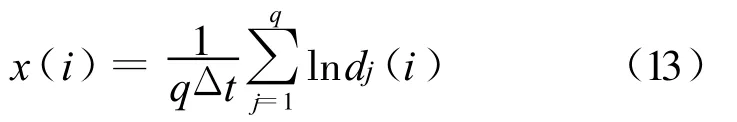
式中,q为d(i)的非零数目,Δt表示相轨迹演变步长。用最小二乘法对 x(i)和i的映射关系进行线性回归,该斜率为最大Lyapunov指数。

5 实验验证与分析

根据非线性动力学相关原理可知,当某一序列的最大Lyapunov指数为正时,可以判定该段信号存在混沌现象。基于此,本文分别对不同类型音频信号频域序列的最大Lyapunov指数进行了统计和分析,相关实验原理如图1所示。

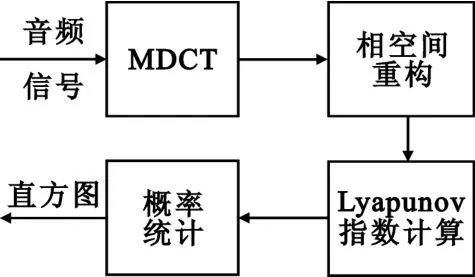
图1 音频频域序列最大Lyapunov指数概率统计原理框图Fig.1 The probability statistic diagram of maximum Lyapunov exponents for audio spectrum series

打击乐音频信号的最大Lyapunov指数曲线和时域波形如图2所示。当音频信号没有声音时,Lyapunov指数维持在一定正值范围内;声音起奏时,Lyapunov指数会迅速下降,但数值仍然为正,然后再返回到最初的数值,总体数值都为正数,所以此音频具有混沌特性。

华觉明:就传统工艺学科建设的建制化而言,工艺美术院校和相关研究机构已相对完善,而其他手工艺的学科建设则相当薄弱甚至有空白之处。必须正视这个事实,敦促主管部门采取措施弥补这一缺陷。专家学者具有专门的学识和广博的视野，能把握方向，起着引领和指导的重要作用。在日本的“无形文化财”中,每一个项目都由一个专家组长期跟踪、调查研究、监管指导。专家提出重要的措施和决策,政府主管部门给予保障,负责实施。在我国,要想尽可能地发挥专家学者的引领和指导作用,基础在于传统工艺的学科建设及传统工艺学科建设的建制化。

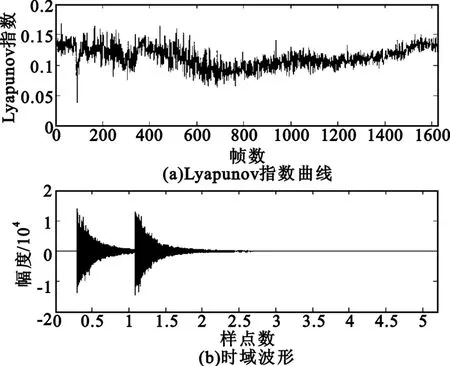
图2 打击乐信号的最大Lyapunov指数曲线和时域波形Fig.2 The maximum Lyapunov exponents curve and time domainwaveform of percussion signal

管乐音频信号的最大Lyapunov指数曲线和时域波形如图3所示。音频信号在从无声到有声突然加载声音时,Lyapunov指数会下降,但仍为正数,随着音频信号的继续输出,Lyapunov指数趋势较为平稳,在个别声音突变处指数会出现向下浮动,负指数通常处在音频过渡或者小能量信号帧中,所占概率不超过5%,图中从统计意义上来看,音频信号的频域序列具有显著的混沌特征。

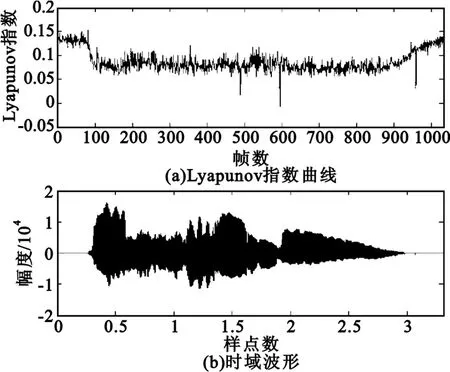
图3 管乐的最大Lyapunov指数曲线和时域波形Fig.3 The maximum Lyapunov exponents curve and time domain waveform of pipe signal

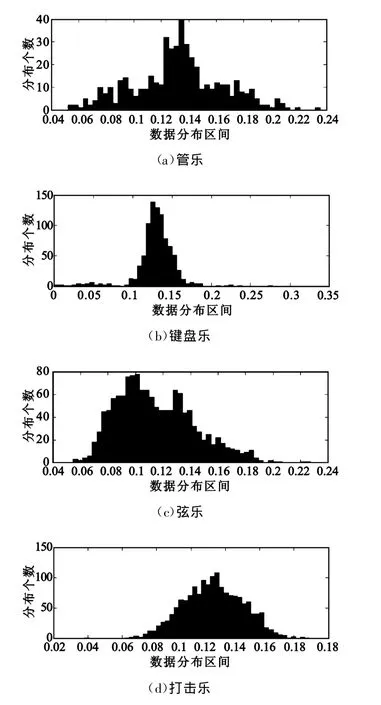
图4 4类音频信号的最大Lyapunov指数统计直方图Fig.4 The histograms of the maximum Lyapunov exponents for four types of audio signals

除了对以上两种器乐音频信号的频域序列最大Lyapunov指数进行了相关统计外,本文还对不同类型音频信号最大Lyapunov指数的分布进行了直方图统计。图4分别表示管乐、键盘乐、弦乐和打击乐的最大Lyapunov指数统计直方图,图5表述了语音信号最大Lyapunov指数的分布情况,可见各个类型的音频信号频谱序列的最大Lyapunov指数均为正数。

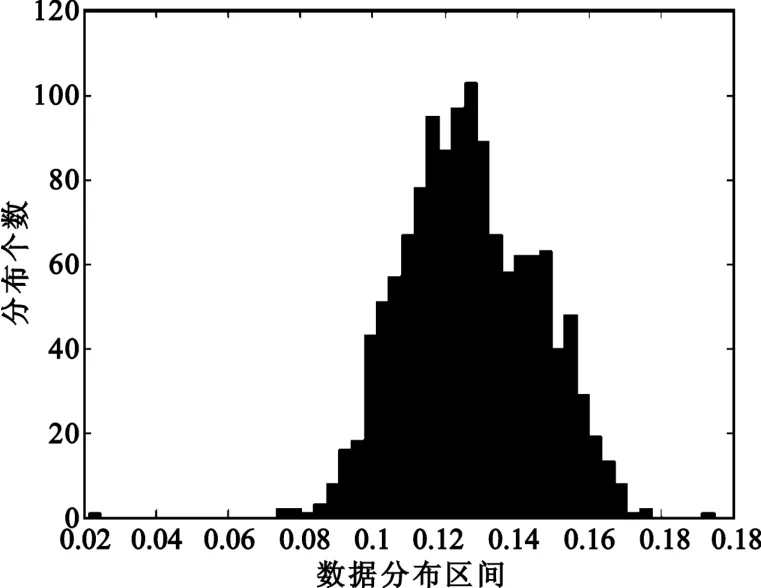
图5 语音信号的最大Lyapunov指数统计直方图Fig.5 The histogram of the maximum Lyapunov exponents for speech signal

为了进一步验证具体器乐音频信号的非线性特性,本文还对音频信号频域序列的平均最大Lyapunov指数进行了统计,如表1所示。

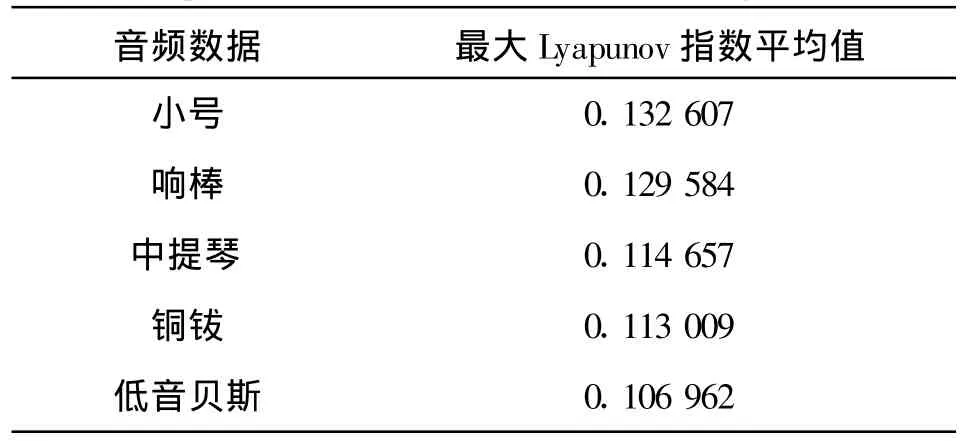
表1 器乐音频信号频域序列的平均最大Lyapunov指数Table 1 The average maximum Lyapunov exponents of the spectrum series for instrumental audio signal

由图4、图5和表1的统计结果可以看出,各段音频信号最大Lyapunov指数分布大于零且平均值也大于零,并未出现负值,即便出现负值,若其概率不超过5%,在统计意义上仍可视此音频信号具有混沌特性。

通过以上实验可以证明,音频信号的频域序列具有典型的非线性特性,这为非线性动力学理论引入音频信号处理领域奠定基础。可以从奇异吸引子重构相空间的角度研究音频系统的动力学特性和本质规律,并利用相关混沌理论对音频信号的频谱进行更加精确地分析、处理和控制,这具有很重要的理论和实际意义。

6 结 论

本文针对音频信号频域信息的非线性特性分析展开研究。首先利用MDCT来对音频信号进行时频分析,并基于时间延迟法利用适当的延迟时间和嵌入维数,重构出音频信号MDCT域信息的相空间,最终实现一种基于最大Lyapunov指数的音频信号MDCT系数混沌特性分析方法。相关统计结果证明,各类音频信号的频谱信息具有明显的非线性特性,这为非线性动力学理论引入音频信号处理领域奠定了基础。

[1] 闫润强.语音信号动力学特性递归分析[D].上海:上海交通大学,2006.YAN Run-qiang.Recurrence Analysis of Dynamical Characteristics for Speech Signals[D].Shanghai:Shanghai Jiaotong University,2006.(in Chinese)

[2] 胡水清,张宇,华一满,等.汉语语音的非线性动力学特性分析[J].声学学报,2000,25(4):329-334.HU Shui-qing,ZHANG Yu,HUA Yi-man,et al.Nonlinear Dynamic Characteristic Analysis of Speech for Chinese[J].Acta Acustica,2000,25(4):329-334.(in Chinese)

[3] 沙永涛.音频频带扩展技术研究[D].北京:北京工业大学,2010.SHA Yong-tao.Research on Bandwidth Extension of Audio Signals[D].Beijing:Beijing University of Technology,2010.(in Chinese)

[4] Yong-tao Sha,Chang-chun Bao,Mao-shen Jia,et al.High frequency reconstruction of audio signal based on chaotic prediction theory[C]//Proceeding of IEEE International Conference on Acoustics Speech and Signal Processing.Dallas,Texas,USA:IEEE,2010:381-384.

[5] Xin Liu,Chang-chun Bao,Mao-shen Jia,et al.Nonlinear Bandwidth Extension based on Nearest-Neighbor Matching[C]//Proceeding of the Second Asia-Pacific Signal and Information Processing Association Annual Summit and Conference.Biopolis,Singapore:APSIPA,2010:169-172.

[6] 许小可.基于非线性分析的海杂波处理与目标检测[D].大连:大连海事大学,2008.XU Xiao-ke.Sea Clutter Processing and Target Detecting Based on Nonlinear Analysis[D].Dalian:Dalian Maritime University,2008.(in Chinese)

[7] 韩敏.混沌时间序列预测理论与方法[M].北京:中国水利水电出版社,2007.HAN Min.Prediction theory and method of chaotic time series[M].Beijing:China Water Power Press,2007.(in Chinese)

[8] 刘秉正,彭建华.非线性动力学[M].北京:高等教育出版社.2004.LIU Bing-zheng,PENG Jian-hua.Nonlinear dynamics[M].Beijing:Higher Education Press,2004.(in Chinese)