双星时差频差无源定位系统定位算法工程指标分析

王勤果,龙 宁

(中国西南电子技术研究所,成都 610036)

1 引 言

双星时差频差无源定位系统是利用两颗卫星通过测量地面同一个辐射源的时差和频差信息来实现对信号的精确定位,具有定位精度高、覆盖区域大、实时性好、对卫星的姿态要求低、系统设备量小等优点。国外在20世纪80年代初就报道了时差频差定位相关技术的研究成果,Stein S在1981年给出了时差和频差的估计精度Cramer-Rao下限和测量方法[1];Ho K C和Chan Y T于1997年对双星时差频差定位算法和多星时差定位算法进行深入研究,并给出了经典的解析求解算法[2];在文献[3]中首次报道了利用时差频差定位成功实现对卫星干扰源的定位。国内许多学者也对时差频差定位相关理论进行了研究[4-7]。但是,国内的研究工作还停留在理论学术研究阶段,没有涉及双星时差频差无源定位系统的工程化相关技术问题,国外文献也没有对其技术细节做详细披露。笔者长期从事双星时差频差无源定位相关理论研究,并对双星时差频差无源定位系统定位算法工程化相关技术问题进行了深入研究。本文针对系统工程化的一个关键技术参数——信号采样时间的选取问题进行了详细论证,并对工程可实现的定位精度进行了理论推导,最后给出了双星系统定位精度效果图。

2 信号采样时间的最优选则

根据对双星定位系统定位精度理论分析可知,时差、频差的测量误差,以及卫星与辐射源之间的空间几何构形及辐射源的固有特性是决定双星定位系统定位精度的关键因素。因此,在双星定位系统工程化中,为了最大限度地提高系统定位精度,应尽量提高时差和频差的测量精度。

文献[1]给出了利用模糊函数估计信号时差和频差的Cramer-Rao下限为

式中,σDTO和 σDFO分别是时差和频差的Cramer-Rao下限,γ1、γ2是两路信号的接收机输出的(射频带宽中)信噪比,BS是信号带宽,B是射频带宽,T是积分时间。

从式(1)中可以看出,信号积分时间、信号带宽及信噪比三项因素决定了信号的时差和频差测量精度。因此,为了最大限度地提高时差和频差测量精度,应尽量增大信号积分时间,即采用长的采样时间。然而,由于低轨卫星运动速度很快,信号的时差和频差是时变的,在较长的采样时间里如果时差和频差变化太大的话,时差和频差测量精度将受较大影响。另外,如果信号采样时间太长,相应的系统硬件代价会过高,也不利于工程化,因此,必须合理选择信号采样时间,以得到最高的时差和频差测量精度。

假定卫星高度为800km,卫星的星间距为100km,信号载频为10GHz,信号的时差变化率和频差变化率如图1和图2所示。从图1中可以看出,由于频差的变化率很大,最大约为15～20 Hz/100ms;从图2中可以看出,时差变化率在100～250 ns/100ms之间。因此,信号的采样时间不宜过长,根据前期系统样机设计经验,考虑高低频段的频差变化率差异很大,采样时间可选为10～100ms。

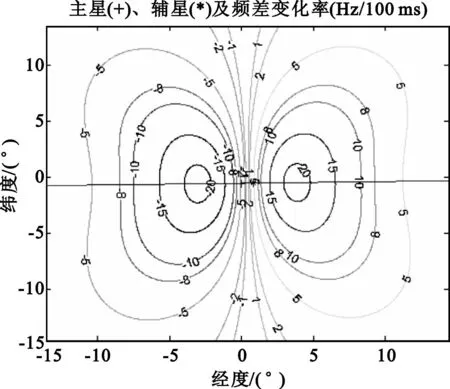
图1 信号的频差变化率分布Fig.1 Signal′s FDOA change rate distribution

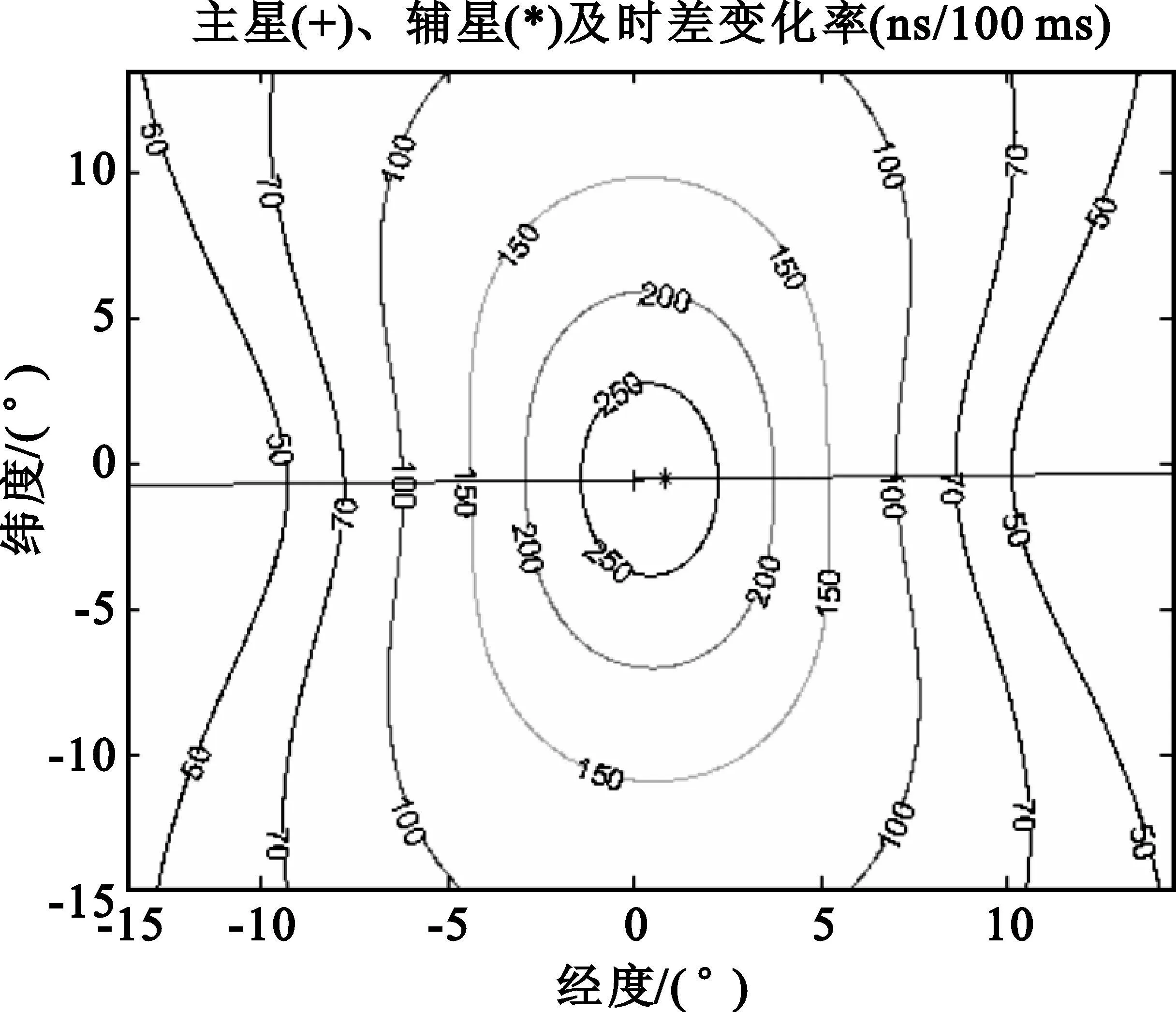
图2 信号的时差变化率分布Fig.2 Signal′s TDOA change rate distribution

图3是卫星对某一辐射源侦察全程信号的时差变化率和频差变化率示意图,从图中可以看出,采样时间在10s内时差和频差都可以看作是线性变化的。对于低重频雷达信号的信号定位,由于需要采用很长的采样时间才能获得较高的时差和频差测量精度,可以采用线性插值的方法修正定位模型以最大限度地提高定位精度。

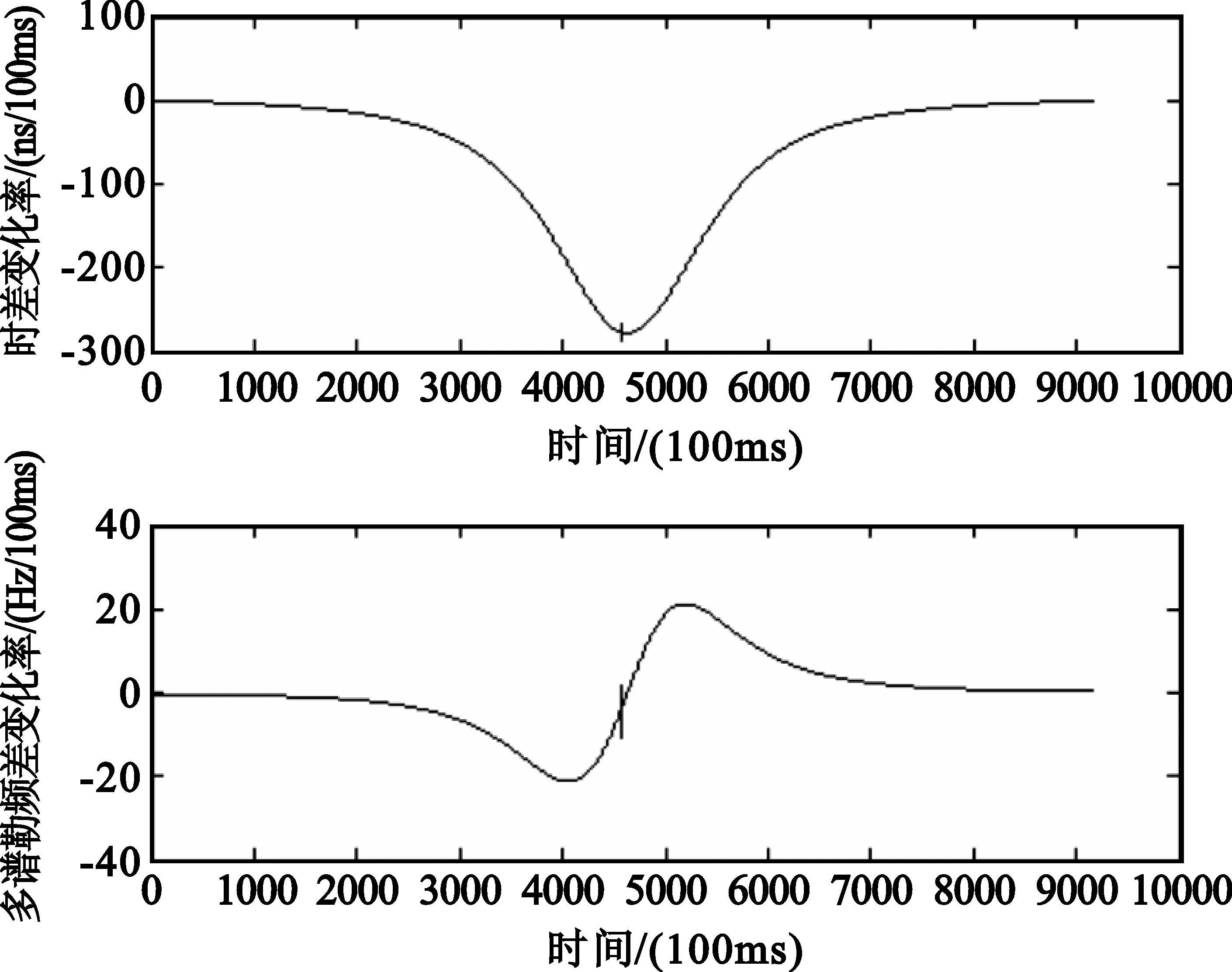
图3 侦察过程中信号的时差、频差变化率Fig.3 Signal′s TD OA and FDOA′s change rate in reconnaissance course

某系统中,信号累积时间为100ms,以主、辅两路信号信噪比均为10dB计,不同的信号带宽下信号时差和频差的Cramer-Rao下限见表1。由表可知,其时差和频差理论测量精度远小于卫星快速运动对时差和频差测量精度的影响。

表1 不同信号带宽的时差和频差Cramer-Rao下限Table 1 TDOA and FDOA′s Cramer-Rao lower limit of different signal bandwidth

3 含卫星站址误差时的双星系统定位精度

定位方程可描述为

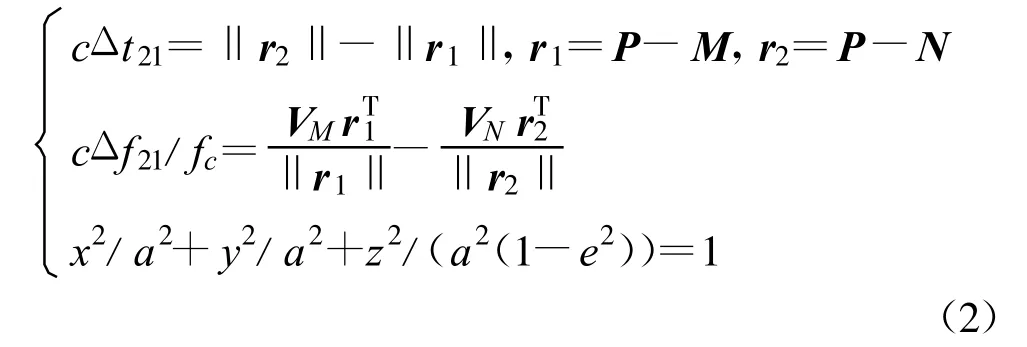
式中,a为地球长轴,e2为第一偏心率平,Δt21和Δf21为时差和频差,fc为信号载频,c为光速。

将定位方程改写为

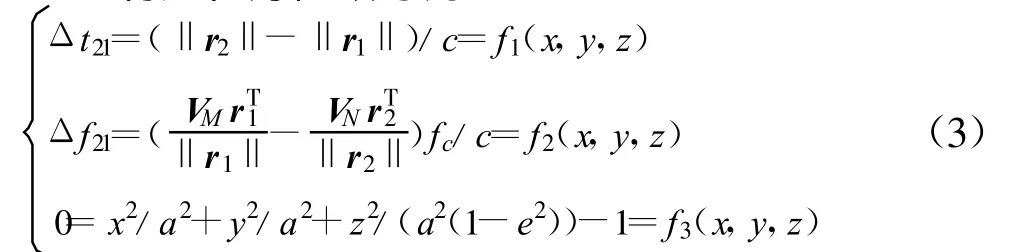
对式(3)微分可得到定位误差协方差矩阵为

式中,E[·]是数学期望算子,dV为观测误差矢量,C为定位系数矩阵,C1、C2为站址系数矩阵,dX为定位误差矢量,dX1、dX2为站址误差矢量,且有:

所以,绝对定位精度的误差几何稀释度:

因此,圆概率定位误差为

式中,tr(·)是求矩阵的迹。类似地,可以推导出考虑卫星速度测量误差时双星系统的圆概率定位误差。

4 双星定位系统工程化可实现的定位精度

图4和图5分别是外场实测的带宽为500kHz的QPSK信号的时差测量误差和频差测量误差分布图,时差和频差测量误差中间值分别为30 ns和0.8 Hz。

图4 时差测量误差分布Fig.4 TDOA measurement error distribution

图5 频差测量误差分布Fig.5 FDOA measurement error distribution

图6 双星系统的圆概率定位误差分布Fig.6 Circular probability orientation error distribution of dual-satellite system

5 结 论

本文分析表明,双星时差频差无源定位系统的信号最佳采样时间为10～100ms,双星系统工程可实现的定位精度约为1～3km。与已经发表过的纯理论研究工作相比,本文对双星定位系统工程化中的定位精度指标的论证与分解具有借鉴意义。为了得到最优的定位性能,需要进一步对双星定位系统的轨道高度、星间距等参数进行优化设计。

[1] Stein S.Algorithms for ambiguity function processing[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1980,29(3):588-599.

[2] Ho K C,Chan Y T.Geolocation of a known altitude object from TDOA and FDOA measurements[J].IEEE Transactions on Aerospace and Electronic Systems,1997,33(3):770-783.

[3] Haworth D P,Smith N G,Bardelli R,et al.Interference localization for EUTELSAT satellites-the first European transmitter location system[J].International Journal of Satellite Communications,1997,15(3):155-183.

[4] 吴世龙,赵永胜,罗景青.双星时差频差联合定位系统性能分析[J].上海航天,2007,2(11):47-50.WU Shi-long,ZHAO Yong-sheng,LUO Jing-qing.Performance Analysis of Dual-Satellite Joint FDOA and TDOA Location System[J].Aerospace Shanghai,2007,2(11):47-50.(in Chinese)

[5] 朱伟强,黄培康,张朝.利用互模糊函数联合估计的双星高精度定位技术[J].系统工程与电子技术,2006,28(9):1294-1298.ZHU Wei-qiang,HUANG Pei-kang,ZHANG Zhao.Two satellite location technology using cross ambiguity function joint estimation[J].Systems Engineering and Electronics,2006,28(9):1294-1298.(in Chinese)

[6] 郭贤生,万群,刘霞,等.数字地图辅助的双星时差频差联合定位方法[J].计算机工程与应用,2006,23(3):11-13.GUO Xian-sheng,WAN Qun,LIU Xia,et al.Digital Map Aided Joint TDOA-FDOA Localization Using Double-star[J].Computer Engineering and Application,2006,23(3):11-13.(in Chinese)

[7] 郭福成,樊昀.双星时差频差联合定位方法及其误差分析[J].宇航学报,2008,29(4):1381-1386.GUO Fu-cheng,FAN Yun.A Method of Dual-Satellites Geolocation Using TDOA and FDOA and Its Precision Analysis[J].Journal of Astronautic,2008,29(4):1381-1386.(in Chinese)