舰舵参数分析仪的设计与实现

韩冰 刘慧 张君臣 杨裕浩

（海军蚌埠士官学校 航海教研室，安徽蚌埠 233000）

1 引言

随着智能化、数字化理论的日新月异，舰船控制趋向于智能化，而舰船运动数学模型参数的确定是进行智能化控制的前提。舰船参数是表征操舵引起舰船航向变化规律的关键参数，也是航向自动舵、航迹自动舵控制器的设计基础，因此舰船参数的正确性直接决定了舰船操纵性能。舰舵参数分析仪能够准确地对舰船参数采集仪[1]的数据的进行处理和辨识，并将辨识结果和舰船运行状况实时显示。具有费用低，适用面广，辨识精度高等特点。

2 设计思路

舰船参数分析仪是一台装有专用数据处理和舰船参数辨识软件的便携式计算机，其工作原理是首先对舰船参数记录仪采集的数据进行筛选，然后以根据已有的舰船操纵运动模型为基础，采用自适应遗传算法对数据进行参数辨识，从而得到舰船参数；同时将参数辨识结果和舰船运行状况进行实时显示。

3 软件设计

舰船参数分析仪的软件设计主要采用模块化设计，它可以分为数据处理模块、参数辨识模块和舰船运行状况实时显示模块。

3.1 数据处理模块

对输入的数据进行筛选，选取有充分激励的数据段进行参数的辨识，这就保证了参数辨识的精度。首先根据已采数据，判断航向是否在单位时间内发生变化，如果发生变化则截取航向发生变化的数据段，否则舍弃。

3.2 参数辨识模块

3.2.1 模型的建立

研究舰船参数，首先必须建立船舶操纵运动的数学模型。基于不同的海况和船舶，人们已经建立起了不同的船舶操纵模型[2]。在这里我们采用三阶线性TK- 方程作为船舶数学模型：

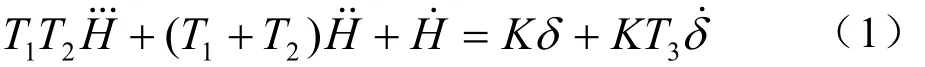
由三阶TK- 方程，得到船舶运动的差分方程为：

在（2）中待辨识的船舶参数有四个，如果增加待辨识船舶的阶数，将会增加待辨识船舶参数的个数。参数增加以后，辨识出的参数之间就会出现相互抵消的现象，降低了辨识精度。因此为了提高辨识算法收敛性和辨识精度，采用三阶K-T方程作为船舶模型是合适的。

式（2）中，a1、a2、b1、b2与K、T1、T2、T3的转换关系：

3.2.2 辨识算法的研究

参数分析仪的核心就是参数辨识算法，迄今为止已有很多种辨识参数的算法例如最小二乘法、间接模型参考自适应法和极大似然法，但这些算法都存在一个致命的弱点就是容易陷入局部最优解。为了克服这一弱点，分析仪采用了一种智能算法—遗传算法。遗传算法是一种基于自然选择和基因遗传学原理的随机并行搜索算法，是一种寻求全局最优解但不需要任何初始化信息的高效优化方法。本文所采用的是一种改进的遗传算法—自适应遗传算法。

3.2.2.1 自适应遗传算法

遗传算法是一种群体型操作，其工作过程是首先产生若干个个体组成的一代群体，由适应度的值决定每个个体进入下一代的机会，再经过遗传操作：选择、交叉、变异算子的作用，产生新一代的个体。不断重复上述过程，在达到预定的目标时终止操作，得到优化结果。

（1）编码

在遗传算法中，采用二进制表示解的强烈偏好通常来自于遗传算法的理论（schema theory），该理论试图用遗传算法的期望模式采样行为来分析算法的性能。然而对连续变量二进制编码实际经验和理论分析明确表明：二进制表示具有严重的缺陷。它通常会在目标函数中引入附加的多峰性，从而使编码后的目标函数比原始问题更为复杂[3]。因此，我们采用实数编码遗传算法。

对于三阶线形K-T方程，我们需要对其中的四个变量即a1、a2、b1、b2，进行编码随机产生初始种群。

（2）适应度函数

（3）遗传算法的三个基本操作

① 选择

采用基于线性排序的适应度分配[4]。排序法克服了按比例适应度计算的尺度问题，在选择压力太大的情况下，由于搜索带迅速变窄而产生的过早收敛。因此，再生范围被局限。排序法引入了种群均匀尺度，提供了控制选择压力的简单有效的方法。同时排序方法比比例方法表现出更好的鲁棒性。因此我们选用排序法来进行选择操作。

② 交叉

交叉是提高遗传算法搜索能力的一个重要操作，是产生新个体的主要方法，而且决定了遗传算法的全局搜索能力[5]；交叉概率cP越大，新个体产生的速度就越快使得具有高适应度的个体结构很快会被破坏；但如果cP过小，会使搜索过程缓慢，一直停滞不前。在此我们引入自适应概念，自适应的cP能够提供相对于某个解的最佳cP。

对交叉进行自适应的调整公式如下：

其中Pc1, Pc2分别为交叉概率的上下限，f1为要交叉的两个个体中较大的适应度，favg为每代群体的平均适应度，fmax为群体中最大适应度值。在此我们选取Pc1=0.9，Pc2=0.06。

③ 变异

变异运算是产生新个体的辅助方法，但它也是必不可少的一个运算步骤，因为它决定了遗传算法的局部搜索能力。与交叉相同，变异也存在变异概率mP选择的问题，如果mP过小，就不易产生新的个体结构；如果mP取值过大，那么GA就变成了单纯的随机搜索算法。因此对变异操作也进行自适应操作。

对变异进行自适应的调整公式如下：

其中Pm1, Pm2分别为变异概率的上下限，f2为要变异的两个个体中较大的适应度，favg为每代群体的平均适应度，fmax为群体中最大适应度值。在此我们选取Pm1=0.1，Pm2=0.001。

表1 实验数据记录表

3.2.2.2 Matlab仿真实验

实验数据采集利用海军工程大学导航工程系研制的“航向自动舵舰-舵模拟器”连接自动操舵仪，形成闭环工作系统，模拟船舶海上运动。利用已研制的“舰舵参数记录仪”，采集航向差HΔ和舵角δ，其中采集时间为0.5 s.

根据“航向自动舵舰-舵模拟器”数据采集的数据进行辨识的数据如表1所示。

从参数辩识的实验数据对比可以看出最小二乘法在对有噪声的数据处理方面已经失去了辨识参数的能力，其中失效的主要原因是在实测的数据中有噪声的干扰；而实验数据可以看出自适应遗传算法还能够对参数进行有效的辨识，这说明了自适应遗传算法具有很强的抗噪能力，这在实际工程应用中具有十分重要的实际意义。

3.3 船型的选择

根据信号采集理论可以知道如果采样时间太大，信号的信息损失过多，将直接影响辨识的精度，有些高阶的过程也会自动退化成低阶的模型，大大降低模型的性能。如果采样时间太小，则除了可能会碰到硬件速度和数值计算出现病态的麻烦外，还会显著影响静态增益的估计值。

因此考虑以上因素在辨识船型上分为大、中、小三种类型时分别对大、中、小船的数据采样时间进行调整，其采样时间分别为0.5 s、1 s、1.5 s。

3.4 船舶运行状态显示模块

为了能够对舰船运行的状态进行实时的显示，设计了这一模块。该模块主要根据舰舵参数记录仪所记录的航向信号、舵角信号以及GPS信号对舰船的航向差、舵角和航速进行实时的显示。

程序流程图如图1所示。

图1 程序流程图

4 软件实现与测试

4.1 软件的实现

软件采用 C++ Builder编写实现参数辨识，并将辨识结果和舰船运行状况实时显示。其中图2航向差、舵角和航速显示的纵坐标分别表示它们的对应数值，横坐标表示采集的时间的序号。

4.2 软件的测试

实验数据采集仍然利用 “航向自动舵舰-舵模拟器”连接自动操舵仪，然后利用本课题研制的“舰舵参数记录仪”，采集航向差HΔ和舵角δ。

图2 辨识结果图

表2 实验数据记录表

对实测数据辨识结果的对比分析可见，K、T辨识参数的相对误差均在15%以内，辨识的效果比较理想。

5 小结

分析仪采用 C++ Builder编写实现自适应遗传算法的参数辨识，并将辨识结果和舰船运行状况实时显示。本系统在进行实际数据的辨识中取得了较好的效果，其辨识相对误差小于15%，解决了以往自动舵模型参数确定没有科学依据的问题，可以满足自动舵开发和调试的需要。产品经过实际应用证明其运行状态良好。

[1] 韩冰, 刘勇. 舰舵参数记录仪的设计与实现[J]. 武汉: 船海工程, 2007（5）: 99-102.

[2] 贾欣乐, 杨盐生. 船舶运动数学模型-机理建模及辨识建模[M].大连: 大连海事大学出版社, 1999:156-161.

[3] Back T, Schwefel H. Evolutionary computation:a survey[M]. Fogel: Kwong S. 1985: 20-28.

[4] 王小平, 曹立明. 遗传算法－理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002: 73－74.

[5] Srinivas N, Kalyanmoy D. Multiobjective optimization using the nondominated sorting in genetic algorithms[J]. Evolutionary Computatio- n.l994, 2（3）; 221－248.