一种新模板的图像边缘提取方法
刘煜,刘岩,吕淑静
(1.西安国家民用航天产业基地管委会卫星应用产业促进局,陕西西安710100;2.第二炮兵工程学院电子技术教研室,陕西西安710025;3华为西安研究所网络产品线,陕西西安710075)
提出了一种基于新模板的图像边缘提取算法,算法依据梯度算子模板的思路,但完全不同于梯度算子,梯度算子是通过模板在待处理图像上按一定规则的遍历,即卷积。首先得到图像的灰度梯度,再设定局部、全局或是自适应阈值,对灰度梯度进行过滤、二值化,得到了图像的边缘。算法的基本原理是:通过设定的水平或垂直模板,与待处理图像进行遍历矩阵相乘,得到图像中相邻像素间的灰度差,接着取定阈值,当灰度差大于该阈值时,将作为灰度差中被减数的像素值赋1,当灰度差小于或等于该阈值时,将相应像素值赋0,即二值化后便得到了图像的边缘[1-3]。
1 纵向模板算法
由算法原理可以看出,本算法最为关键的就是模板的选取。现在选定一个3×3的纵向模板
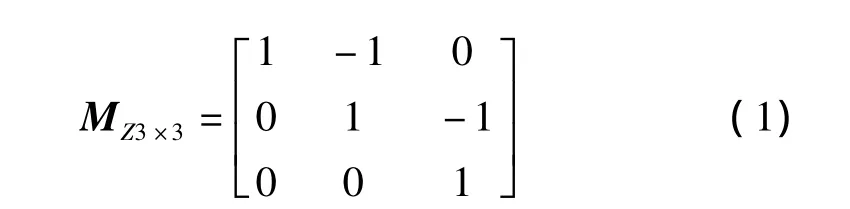
设G为待处理图像,当MZ3×3在G上遍历相乘时有
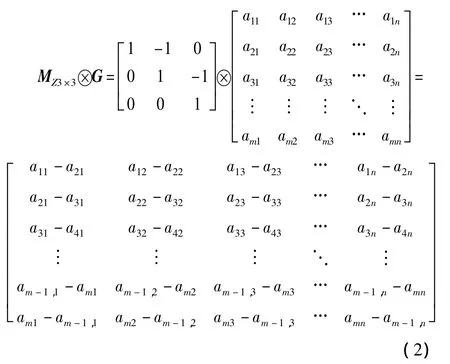
式(2)中“⊗”表示遍历相乘,注意到结果矩阵的第m-1行和第m行中各对应元素绝对值相等且互为相反数,这是因为m行是结果矩阵的最后一行,无法向下相减,便用向上相减替代之。因为图像中相邻元素间属性的相似性,所以这种替代是合理的。用表示式(2)矩阵中的元素,其中1≤i≤m,时,将aij的灰度值置为,将aij的灰度值置为0,这样就得到了采用纵向3×3模板算法时图像G的多像素二值边缘图。所谓的纵向模板算法,是指MZ3×3在图像G上遍历矩阵相乘后,得到的是G的纵向灰度差,即相邻行之间的灰度差。式(2)中M为选取的阈值,采用类间方差最大化阈值分割算法(Otsu)得到[4-7]。
采用Matlab语言编程、选择某机场下视景图像对提出的纵向3×3模板算法进行计算机仿真实验。图1(a)为265×351的某机场原始的下视景图像,图1(b)为采用该算法对边缘提取的结果。

图1 Prewitt算子及纵向模板算法提取边缘的结果
从仿真结果可以看出:与Prewitt算子相比,纵向模板算法对图像中背景和目标对比度较小的部分边缘提取较为完整,对于图像中的辅道边缘,算法未能完整提取。从整体效果上讲,算法对机场下视景图像边缘的提取要优于Prewitt梯度算子。
为提高边缘提取的速度,可以将模板尺寸放大,有下面的5×5纵向模板和7×7纵向模板,

采用这两个模板提取图像边缘的算法原理与MZ3×3相同。
接着使用Matlab语言编程,为便于对照,仍然选择某机场下视景图像对提出的纵向5×5模板算法和纵向7×7模板算法进行仿真实验。图2(a)为265×351的某机场原始图像,为便于对比,将纵向3×3模板算法结果置放于此,如图2(b)所示。图2(c)为采用纵向5×5模板算法对边缘提取的结果,图2(d)为采用纵向7×7模板算法对边缘提取的结果。

图2 纵向模板算法提取边缘的结果
从仿真结果可以看出:3种模板对机场下视景图像边缘的提取均较为完整,整体效果相当,只是随着模板尺度的增加,边缘图像稍有模糊。
下面,对这3种算法边缘提取的时间开销情况予以分析。图3(a)中分别对3种纵向模板进行了10次随机的耗时量统计,如横轴所示,纵轴表示对应的开销时间。
从图3可以看出:纵向7×7模板算法耗时最少,10次耗时均值为0.53 s;纵向5×5模板算法次之,耗时均值为0.62 s;纵向3×3模板算法花费时间最长,耗时均值为1.00 s。即随着纵向模板尺度的增大,提取图像边缘的时间减小。
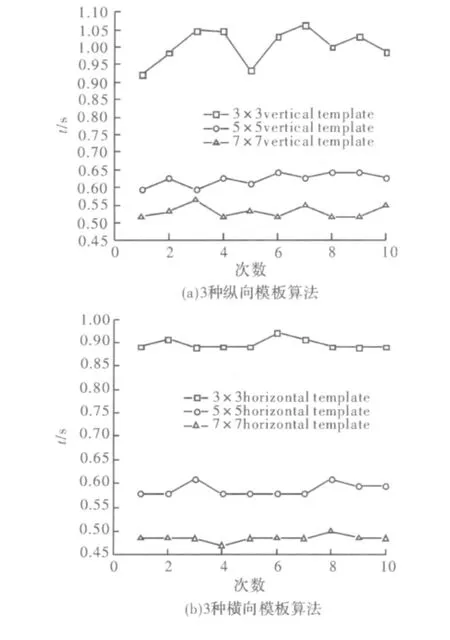
图3 纵、横向模板算法耗时比较
2 横向模板算法
横向模板算法中的“横向”,是指模板在图像上遍历矩阵相乘后,得到的是图像的横向灰度差,即相邻列之间的灰度差。
各种尺度的横向模板如下所示

在纵向模板算法中,是以模板MZ左乘图像G的,而在横向模板算法中,Mh则是右乘图像G的,
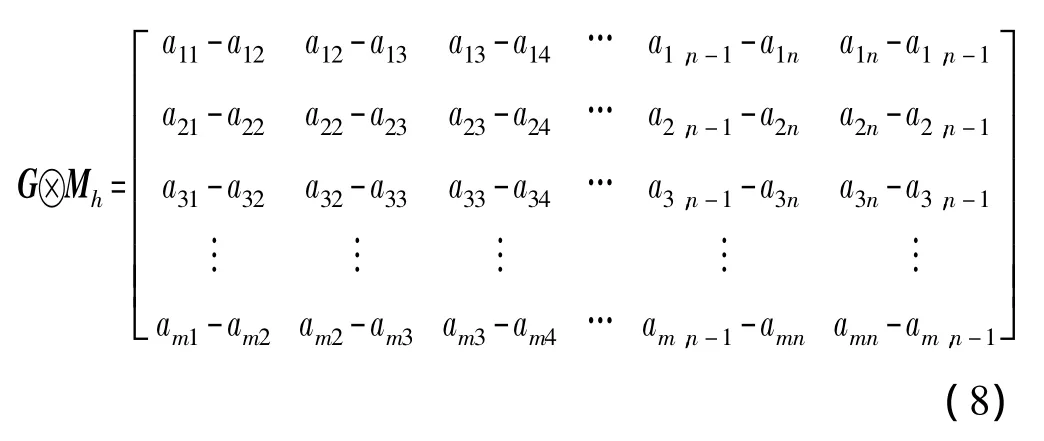
式(8)中“⊗”表示遍历相乘,注意到结果矩阵的第n-1列和第n列中的各个对应元素绝对值相等且互为相反数,这是因为第n列是结果矩阵的最后一列,无法向后相减,便用向前相减替代之。用表示式(8)矩阵中的元素,其中1≤i≤m,时,将aij的灰度值置将aij的灰度值置为0,这样就得到了采用横向模板算法时图像G的多像素二值边缘图。式中阈值M的选取方法与式(2)相同。
使用Matlab语言编程,对提出的横向模板算法进行仿真实验。为便于对比,将纵向3×3模板算法结果置放于此,如图4(a)所示,图4(b)为采用横向3×3模板算法对边缘提取的结果,图4(c)为采用横向5×5模板算法对边缘提取的结果,图4(d)为采用横向7×7模板算法对边缘提取的结果。

图4 横向模板算法提取边缘的结果
由实验结果可以看出:横向3×3模板算法的边缘提取效果优于纵向3×3模板算法。这一点可以由位于右侧的斜向贯穿图像上下的辅道看出,纵向模板算法几乎未提取到该边缘,而横向模板算法对该边缘提取得较为完整;横向3种模板算法对机场边缘提取效果相当,均较完整地检测到了图像边缘。
下面,对这3种横向模板算法边缘提取的时间开销情况进行分析。图3(b)中分别对3种纵向模板进行了10次随机的耗时量统计,如横轴所示,纵轴表示对应的开销时间。
从该图可以看出:横向7×7模板算法耗时最少,10次耗时均值为0.48 s;横向5×5模板算法次之,耗时均值为0.59 s;横向3×3模板算法花费时间最长,耗时均值为0.89 s。整体上,横向模板算法的耗时量要小于纵向模板。这是因为该下视景机场图像265×351的尺寸格式所致,其行数少于列数,故横向时耗时少,纵向时耗时多。
由以上分析可知,无论是纵向模板算法还是横向模板算法,其对下视景机场图像边缘的提取都要优于梯度算子,从耗时角度讲,纵、横向模板算法与Prewitt梯度算子相当。因此,对纵、横向模板算法提出以下改进算法。
3 纵向和横向模板算法的改进
在前述算法中,依据梯度算子模板的思路,提出了纵向和横向模板算法的N×N,N=3,5,7模板,但注意到当采用纵向模板算法时,模板中的最后一行没有起到算法目的,只是将原像素值再次赋给了当前像素点。同理,当采用横向模板算法时,模板中的最后一列亦没有起到算法目的[8]。
针对以上算法缺点,在纵向模板算法中可以将对算法没有贡献的最后一行去掉,这时,相应模板改变为
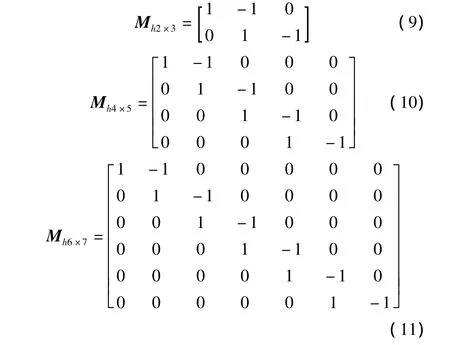
同理,在横向模板算法中可以将对算法没有贡献的最后一列去掉,这时,相应模板改变为
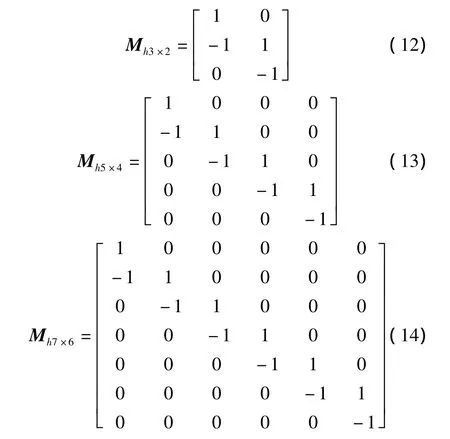
对改进后算法进行仿真,结果显示,边缘提取效果与改进前几乎没有差别,所以在此不再列显边缘提取效果,但耗时情况有所改善,具体情况见图5。图5(a)是纵向模板算法改进前后的耗时情况对比,图5(b)是横向模板算法改进前后的耗时情况对比。
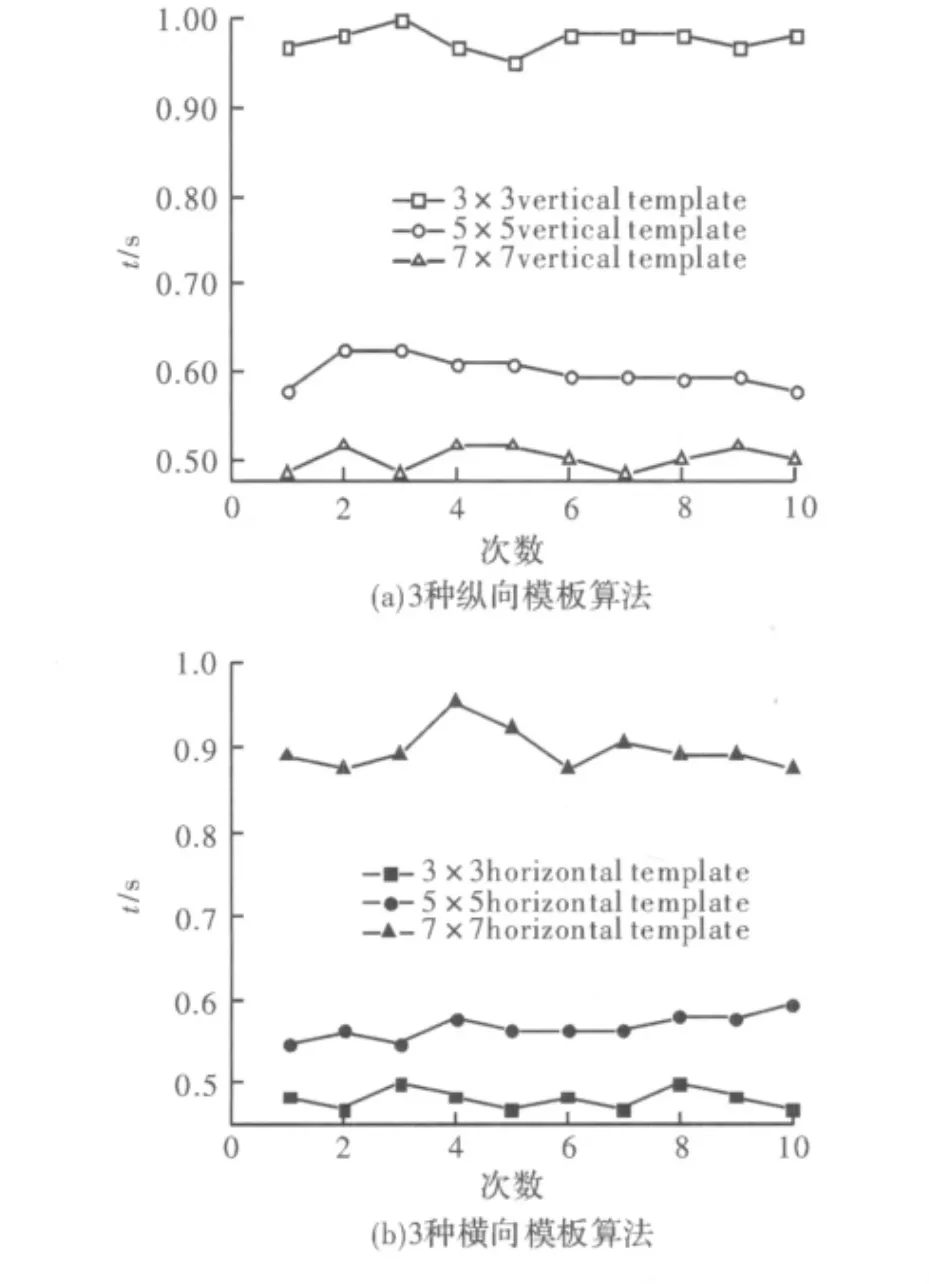
图5 模板算法改进前后耗时比较
由图5(a)可以看出,纵向7×7模板算法耗时最少,10次耗时均值为0.50 s;纵向5×5模板算法次之,耗时均值为0.6 s;纵向3×3模板算法花费时间最长,耗时均值为0.98 s;由图5(b)可以看出,横向7×7模板算法耗时最少,10次耗时均值为0.45 s;横向5×5模板算法次之,耗时均值为0.57 s;横向3×3模板算法花费时间最长,耗时均值为0.84 s,如表1所示。
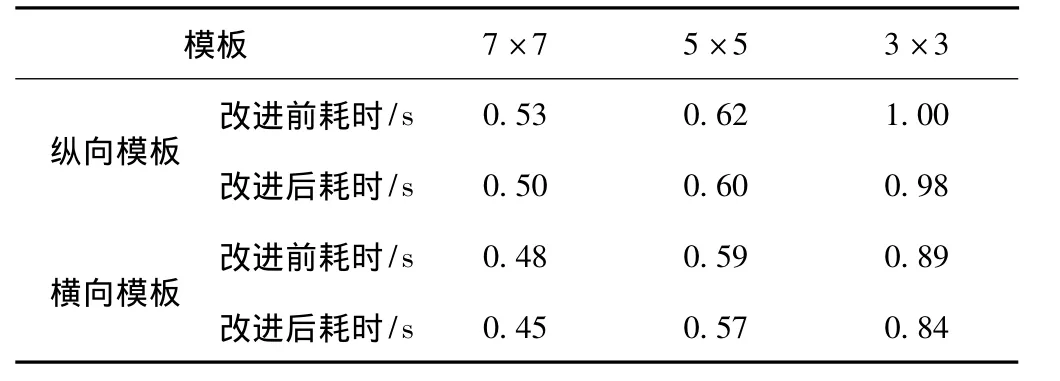
表1 纵、横向模板算法改进前后耗时对比
表1反映了模板算法改进前后的时间花费情况,对于纵向模板算法,改进后平均耗时减少了3.3%,横向模板算法改进后平均耗时减少了4.6%。
4 结束语
提出了一种基于新模板提取图像边缘的方法,并基于该方法的实际机理,从提取图像边缘的耗时方面进行了有益改进。从实验结果得到以下结论:(1)利用纵、横模板提取图像边缘的方法,采用Matlab语言编程对1幅265×351大小的图像进行边缘提取时,效果要优于Prewitt算法,且耗时与其相当,仅为0.48~0.53 s。(2)针对边缘提取的时间优化,对纵、横模板提取图像边缘的方法进行了改进,在保证提取图像边缘信息几乎不变的情况下,将纵、横模板提取图像边缘的时间分别减少了3.3%和4.6%。(3)提出的纵、横模板提取图像边缘的方法,具有模型简单且实时性强等特点。对于图像边缘实时提取领域的开发和研究,以及利用该算法对图像定位与匹配等领域进一步的研究,具有一定意义。
[1] BEHZAD K P,BEHROOZ K P,AZRIEL R.Optimally isotropic laplacian operator[J].IEEE Transactions on Image Processing,1999,8(10):1467-1472.
[2] MEJJAOLI H,TRIMECHE K.On a mean value property associated with the dunkl laplacian operator andapplications[J].Integral Transforms and Special Functions,2001,12(3):279-302.
[3] 刘煜.飞行器下视景像预处理及实时匹配技术研究[D].西安:西北工业大学,2007.
[4] 梁光明,孙即祥,马琦,等.Ostu算法在Canny算子中的应用[J].国防科技大学学报,2003,25(5):36-39.
[5] 岳振军,邱望成,刘春林.一种自适应的多目标图像分割方法[J].中国图象图形学报:A辑,2004,9(6):674-678.
[6] 杜健辉,吕文阁,侯梦华.基于竞选算法的Otsu阈值快速确定方法[J].机电工程技术,2007,36(3):57-58.
[7] 任继军.基于灰度空间自动阈值选取的彩色舌图像分割算法[J].陕西科技大学学报:自然科学版,2005,23(2):73-77.
[8] 刘煜,李言俊,张科.一种多像素图像边缘提取方法[J].光子学报,2007,36(2):380-383.

