三坐标测量机长度测量不确定度评定

曹雪梅,陈晓怀,李红莉

(合肥工业大学 仪器科学与光电工程学院,合肥 230009)

0 引 言

测量不确定度是评价测量结果质量的重要指标。由ISO等7个国际组织制订并颁布实施的《测量不确定度表示指南》(简称为GUM)定义:“测量不确定度表征合理地赋予被测量值的分散性,是测量结果含有的一个参数”。没有不确定度的测量结果是不完整的、没有意义的、不具有实用价值的。现有的三坐标测量机在应用时,通常得到的只是被测参数的估计值,而没有给出相应的测量不确定度[1]。

三坐标测量机在应用中引起被测参数不确定度的来源非常复杂,它不仅与测量机本身的精度有关,还与采样策略、被测工件、环境条件及数据处理方法等一系列因素有关。本文根据最新国际标准JCGM 101-2008:测量不确定度表示指南附录1建立相应的数学模型,重点探讨坐标测量机进行长度测量的不确定度评定。该模型也可推广应用到其他测量任务如直线度、平面度、圆度等形位误差的不确定度评定,使得三坐标测量机在实际应用中得到测量值和不确定度估计的完整测量结果报告,提高三坐标测量机测量结果的准确度和可信度。

1 测量模型

三坐标测量机测量量块几何尺寸一般是通过间接测量的方法得到的,即在量块上建立坐标系,在其一个测量端面上任取多点Pi(i=1,…,N,要求N≥3),求测量长度方向上的两端面中心点之间的距离。本文从测量策略考虑,先在一个测量端面上任取n个点Pi(i=1,…,N,要求N≥3),利用各测量点到平面的距离的平方和为最小值确定最小二乘拟合平面V;再在其相对另一测量端面的中心位置区域任取一点Pk;从而求出Pk(xk,yk, zk)点到拟合平面V的距离L,即为量块长度,见图1[2]。

图1 量块长度测量模型示意图Fig.1 Schematic diagram of the measurement of the amount of block length

假定Pi(i=1,…,N)为N个测量点,最小二乘拟合平面为:

其中a,b,c为待定参数。

由正规方程:

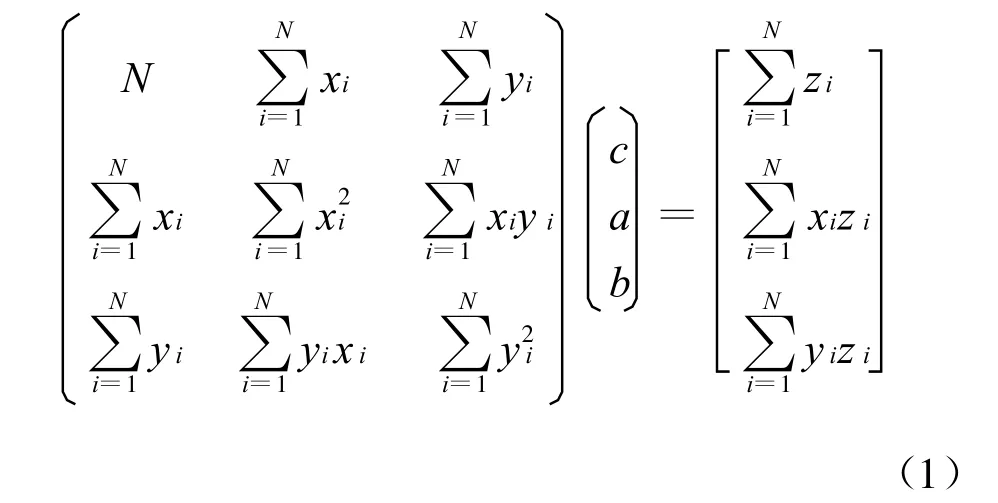
根据最小二乘原理计算最小二乘平面的待定参数a,b,c为[3]:

则Pk点到拟合平面V的距离计算公式为:

2 误差模型

国家标准GB/T 24635.3中指出,三坐标测量机的测量过程中存在多种测量因素对测量结果带来影响,主要包括:①测量重复性误差;②机构误差;③力变形误差;④热变形误差;⑤探测系统误差;⑥动态测量误差。

其中,机构误差包括定位误差(标尺读数系统的误差和阿贝误差)、直线度运动误差和角运动误差。测量重复性误差和机构误差直接影响测量点的坐标值,其他误差来源则是对最终测量结果产生影响[4]。

因此量块长度测量长度模型可表示为[5]:

式中l为量块长度测量模型计算结果;αs为量块的热膨胀系数;Δθ为实际测量环境温度与要求标准测量环境温度之差;δ lr es为测量机的探测误差;δ lr为测量机的力变形误差;δ lv为测量机的动态误差。

建立误差传递链函数:

通过该传递链函数,可以将测量过程模拟地处理成一序列信号处理模块。单个模块将输入信号yi-1和各种误差输入量处理成输出量yi,方便下面利用蒙特卡罗法进行不确定度评定。同时,传统的误差评定模型,每增加一个误差源分析,则需要重新建立误差传递模型,非常繁琐。建立该传递链函数,可以保留误差来源的核心部分y1=l(1-αsΔθ)不变,其他误差来源以增加传递链的形式增加,在实际误差评定中更具有广泛应用性。

3 不确定度评定模型

由误差传递链函数式(4)可以得到:

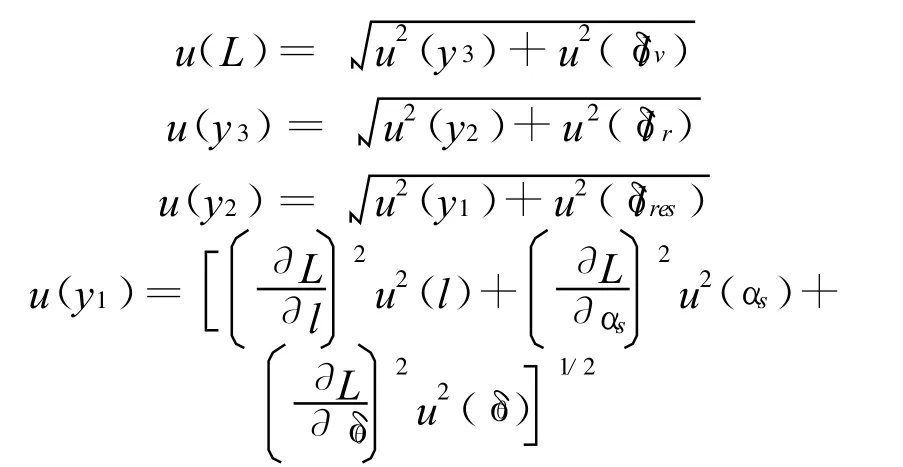
各传递系数:

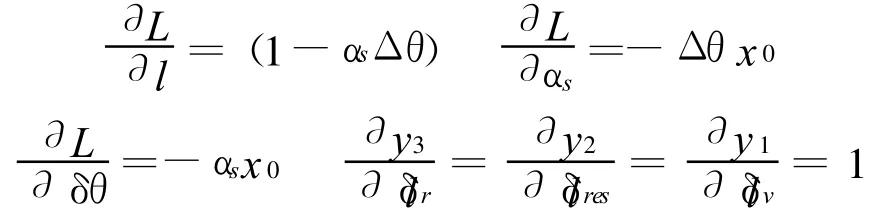
因此量块测量几何长度L的测量不确定度为:

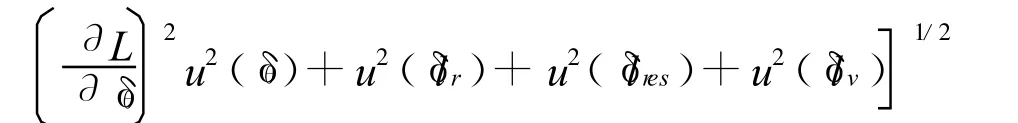
其中量块长度测量模型引起的不确定度分量u(l)可根据Pk点到拟合平面V的距离计算公式同理分析得到。

由式 (2)可知l=g(xk,yk,zk,a,b,c)。其输入量 xk、yk、zk互不相关;a、b、c互相之间相关性弱,在此不考虑。

根据GUM不确定度传播定律,求得各传递系数:

式中u(xk)、u(yk)、u(zk)的不确定度由重复性测量和坐标测量机的机构误差构成:

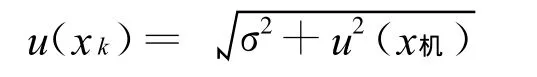
计算u(a)u(b)u(c)。由平面拟合回归方程知,估计量 a,b,c的协方差为:D¯b= (ATA)-1σ2。

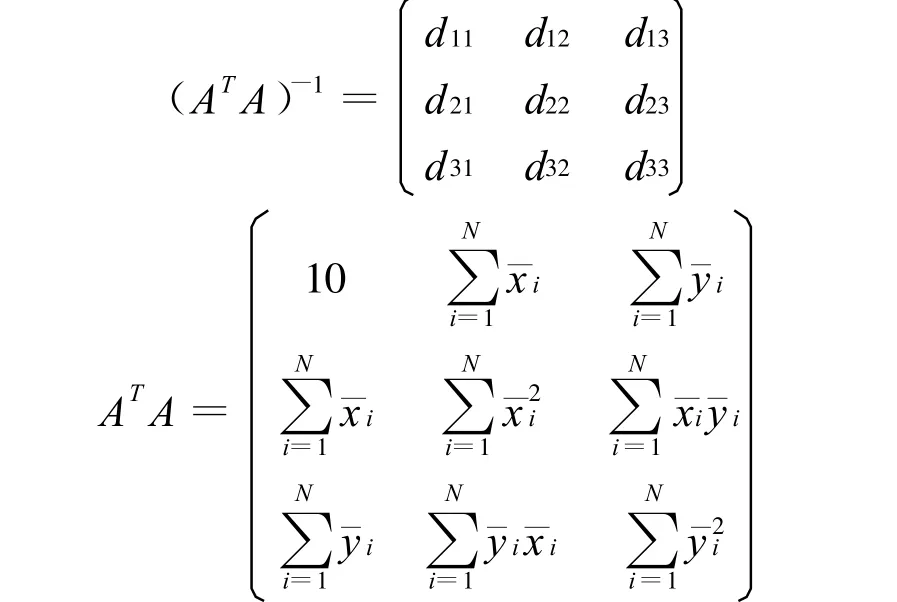
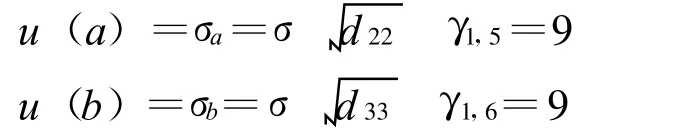
综上,即可得到量块长度测量L的不确定度。

4 实验数据处理

在MH3D-DCC型坐标测量机上对标称长度为100 mm的0级标准量块进行测量,综合考虑各误差来源对测量结果的影响,根据量块尺寸测量模型:

由式(2)计算得出l=100.007 mm

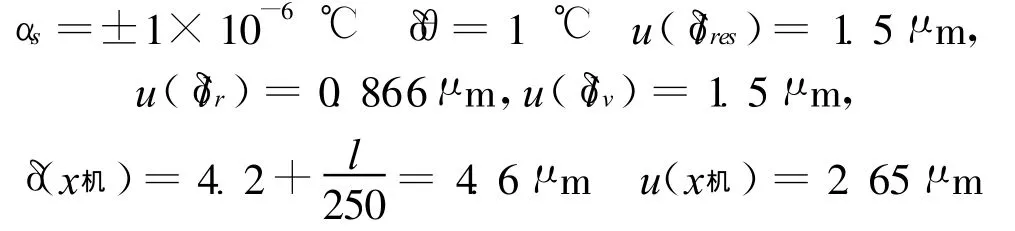
代入测量模型,可得量块长度测量的不确定度为u(L)=0.010 mm

根据蒙特卡罗法应用于三坐标测量机测量不确定度评定的基本原理和方法[6],使用LABVIEW软件对测量数据进行处理,得到测量结果见表1。

表1 蒙特卡罗法与GUM评定方法结果比较Table 1 Compared the results of Monte Carlo method and GUM method

由上表可见,基于GUM原理构建坐标测量机长度测量的不确定度评定模型,以及基于蒙特卡罗法应用计算机软件进行模拟评定,这两种不确定度评定方法的结果比较一致,表明此不确定度评定模型较为准确,可以应用于坐标测量机尺寸测量的不确定度评定中。

5 结 语

本文所提出的不确定度评定模型是基于GUM的不确定度评定原理而构建的 ,它综合考虑了三坐标测量机进行尺寸测量时自身误差和测量过程中引入的各项误差,并且通过与蒙特卡罗模拟方法的不确定度评定结果相比较,验证了此模型的准确性。文中应用了传递链函数构建模型,使得此模型可应用于各种测量环境下的三坐标测量机测量任务的不确定度评定,改变误差源时只需对传递链进行调整,无需重新建立数学模型,实际应用时十分简便。此模型还可推广应用到直线度、平面度、圆度等多种形位误差的测量结果不确定度评定中,从而实现三坐标测量机测量值和不确定度估计的完整报告,提高三坐标测量机测量结果的准确度和可信度。

[1]国际标准化组织.测量不确定度表示指南[M].刘智敏,刘增明译,北京:标准化文摘杂志社出版,1995.

[2]王金星,蒋向前,马利民.平面度坐标测量的不确定度计算[J].中国机械工程,2005,16(19):1 701-1 703.

[3]费业泰,误差理论与数据处理 [M].北京:机械工业出版社,2008.

[4]GB/T 24635.3产品几何技术规范 (GPS)坐标测量机(CM M)确定测量不确定度的技术第3部分:应用已校准工件或标准件 [S].北京:中国标准出版社, 2009.

[5]JCGM 101:2008 Evaluation of measurement data—Supplement 1 to the“Guide to the expression of uncertainty in measurement”— Propagation of distributions using a Monte Carlo method[S].JCGM-WG1,2008.

[6]陈晓怀,薄晓静,王宏涛.基于蒙特卡罗方法的测量不确定度合成 [J].仪器仪表学报,2005,26(S1): 759-761.