部分端板连接梁柱组合节点有限元分析

刘洪波,赵文军,魏振兴,霍振兴,柳艳杰,孙 静,吕兴群

(1.黑龙江大学 建筑工程学院,哈尔滨 150080;2.中国石油东北炼化工程有限公司 吉林设计院,吉林 132002;3.吉林省建筑设计院有限责任公司,长春 130011)

0 引 言

端板连接的钢框架梁柱组合节点,以其构造简单、受力性能好等优点在实际工程中得到广泛应用。部分端板连接的钢框架梁柱节点可以作为端板连接的特例,其构造更为简单。传统上一直以铰接的理想假定对其进行刚度及承载力分析,而实际上这种理想假定是很难实现的,特别是考虑楼板对其影响时,刚度和承载力都会大幅提高,其力学分析模型应该是一种半刚性连接形式[1-2]。

本文将在前人对于半刚性节点分析的基础上,针对部分端板连接组合节点的特殊形式,着重考虑楼板参与工作对节点性能的影响,并探讨各影响因素对于这一节点形式的影响规律。

1 有限元模型建立

部分端板连接组合节点采用三维实体模型建立。使用ANSYS软件进行有限元分析时,钢构件(梁、柱、端板及螺栓)用SOLID45单元模拟;楼板用SOLID65单元模拟,采用整体式模型考虑钢筋性能,并设定混凝土受拉开裂后退出工作;混凝土和钢材采用双线性随动强化 (BKIN)模型,为加强模型计算收敛,钢材达到屈服强度后考虑5/ 1 000倍弹性模量的应力强化,混凝土采用多线性等向强化(MISO)模型;端板与柱翼缘、螺栓侧壁与螺栓孔以及楼板与钢梁之间的接触采用TARGE170和CONTA173单元模拟;此外,采用PRETS179单元模拟高强螺栓的预拉力。

为了验证本文有限元模型建立方法的可应用性,建立文献 [3]所介绍试验的有限元模型,并与其结果进行比较。图1为有限元计算与试验所得的弯矩转角关系曲线,由图1可见,本文所建模型可以很好地模拟部分端板连接组合节点的性能。

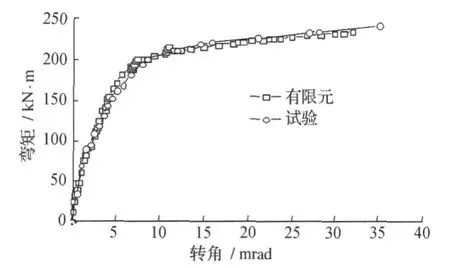
图1 有限元与实验数据对比Fig.1 Comparison between measured and computed

2 参数分析

2.1 标准试件参数

进行ANSYS有限元分析,需要变换构件参数,选取一个变换参数的标准模型试件可减少计算,有利于分析对比。本文选取 “标准试件”各构件几何及材料特征见表1,几何尺寸示意图见图2。本文暂不研究剪力栓钉作用,不对栓钉作特殊规定,其特性与试验一致,按全部强度设计。根据《欧洲规范》,楼板宽度取3倍钢梁高度。

对于节点性能的分析以上述试件为基准,变换适当参数进行。为此,将上述节点定义为 “标准试件”或称为 “1号试件”,在下面各组分析中分别以 “A1、B1、C1……”表示。

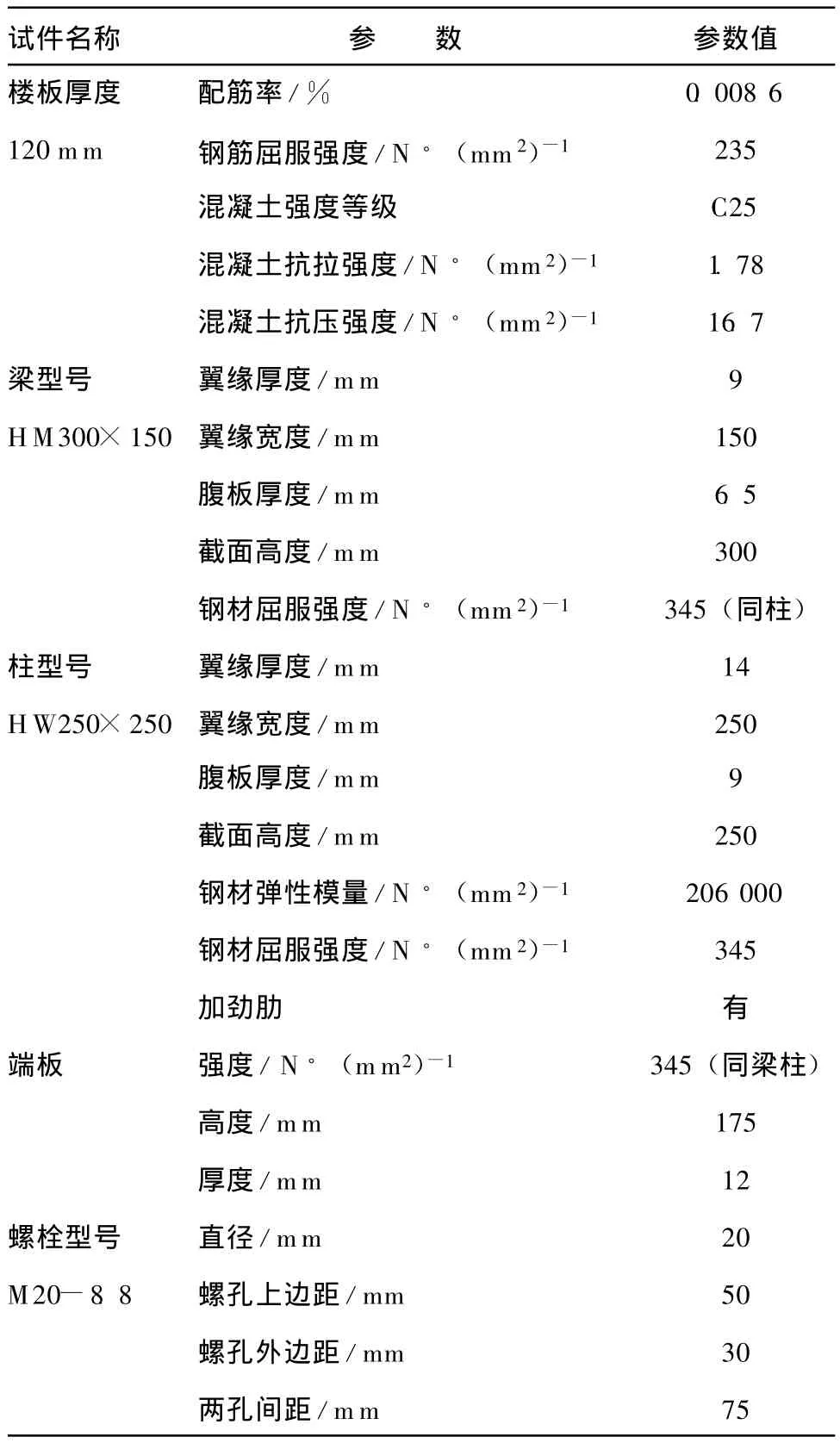
表1 “标准试件”特性参数Table 1 Properties of members

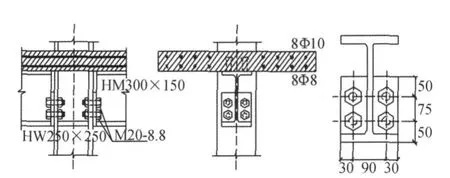
图2 “标准试件”构造特征Fig.2 Details of members

2.2 楼板配筋率的影响

针对节点配筋率的研究,变换不同配筋率设计A组共计4个试件,A1～A4对应配筋率分别为0.008 6、0.012 8、0.017 8、0.023 7。

A组试件弯矩转角关系见图3(a),从图中可以看出,节点的初始刚度、弹性抗弯承载力和塑性抗弯承载力均随着钢筋直径的增加而增加。

从A4与A1的比较可知,配筋率提高175.6%,初始刚度提高59.4%,强化刚度提高24.2%,弹性弯矩提高153.0%,塑性弯矩提高104.0%。可见,配筋率的变化对于强度和刚度的影响都很显著,是提高强度和刚度的有效办法。虽然在配筋率的影响下,节点的强化刚度有提高,但由于基数小,其对节点性能的影响很小。

2.3 钢筋屈服强度的影响

针对于节点钢筋种类的研究,变换不同钢筋种类设计B组共计3个试件,B1～B3分别对应屈服强度235、335、400 MPa。

B组试件弯矩转角关系见图3(b),由图 3 (b)可见,节点的弹性抗弯承载力和塑性抗弯承载力均随钢筋强度提高而增加。但节点的刚度变化不大。

从B3与B1的比较可知,钢筋强度提高70.2%,弹性弯矩提高57.5%,塑性弯矩提高47.8%。可见,钢筋强度的变化对于节点强度的影响显著,是提高节点强度的有效办法。

2.4 楼板混凝土强度等级的影响

作为楼板性能的又一重要影响因素,混凝土作用不可忽视。选取建筑楼板中常用的4种混凝土类型设计C组4个试件,C1～C4分别对应C20、C25、C30、C35。4个试件节点弯矩转角关系见图3(c),由图3(c)可见,混凝土的强度等级对节点强度和刚度的影响都不大。这主要是因为混凝土受拉会在早期退出工作。

2.5 梁柱屈服强度的影响

梁柱钢材的屈服强度,对中和轴的位置,节点的破坏模式都有影响。选取建筑钢材中常用的4种强度设计D组4个试件,D1～D4分别对应Q345、Q235、Q390、Q420。

4个试件节点弯矩转角关系见图3(d),由图3(d)可见,随着钢材屈服强度的提高,节点的刚度没有较明显的变化,节点的强度略有增长。

从D4与D2的比较可知,钢材的屈服强度提高78.7%,塑性弯矩仅提高8.0%。可见,钢材的屈服强度对节点承载力影响不大。这主要是由于节点的破坏模式主要是钢筋和螺栓区域的屈服,梁柱钢材强度的提高只能使螺栓区域的屈服进一步发展,对承载力的影响显然会小。这样,在设计中,破坏模式一般不依赖于梁柱强度,Q235钢材已经能够基本满足节点承载力需要。

2.6 钢梁截面高度的影响

钢梁的截面高度,对中和轴的位置会有显著影响,进而影响到节点的破坏模式。在型钢梁HM300×150基础上,变换梁高设计了E组4个试件,E1～E4分别对应梁高300、250、350、400 mm。

元人作剧，曲中用事，每不拘时代先后。马东篱《三醉岳阳楼》，赋吕纯阳事也。【寄生草】曲：“这的是烧猪佛印待东坡，抵多少驹驴魏野逢潘阆”。俗子见之，有不訾以为传唐人用宋事耶？画家谓王摩诘以牡丹、芙蓉、莲花同画一景，画《袁安高卧图》有雪里芭蕉，此不可易与人道也。[18](P147-148)

4个试件节点弯矩转角关系见图3(e),由图3(e)可见,随着钢梁的截面高度的增加,节点的初始刚度、弹性抗弯承载力和塑性抗弯承载力均随之增加。

从E4与E2的比较可知,钢梁的截面高度提高60.0%,初始刚度提高129.7%,弹性弯矩提高34.9%,塑性弯矩提高45.4%。可见,钢梁的截面高度的变化对于强度和刚度的影响都很显著,是提高节点各方面性能的很有效办法。

2.7 端板厚度的影响

梁柱连接端板厚度,对螺栓受拉区域破坏模式有显著影响,进而影响到节点的承载力。变换端板厚度设计了F组4个试件,F1～F4分别对应短板厚度为12、10、15、20 mm。

4个试件节点弯矩转角关系见图3(f),由图3 (f)可见,随着端板厚度的增加,节点的初始刚度基本不变、弹性抗弯承载力和塑性抗弯承载力的增加幅度也很小。

从F4与 F2的比较可知,端板厚度提高100.0%,初始刚度和弹性弯矩基本保持不变,塑性弯矩也只提高了16.9%。端板厚度的变化对于强度和刚度的影响都很小,只是判定端板是否破坏的判定依据。一般说来,端板厚度大于柱翼缘厚度时,节点破坏时可保证端板不被破坏。随着端板厚度的增加,其塑性弯矩增加幅度变小,就是因为端板厚度已经超过了柱翼缘的厚度,破坏模式由端板的破坏转为柱翼缘的破坏,这在设计中是不利的[4]。

2.8 端板高度(螺栓孔间距)的影响

梁柱连接端板高度,一定程度上决定着螺栓孔的间距,对螺栓受拉区域破坏模式及中和轴的位置都有显著影响,进而影响到节点的性能。变换端板高度设计了G组4个试件,G1～G4分别对应端板高度175、150、200、250 mm。

4个试件节点弯矩转角关系见图3(g),由图3(g)中可见,随着端板高度的增加,节点的初始刚度、弹性抗弯承载力变化不大,塑性抗弯承载力随之增加。

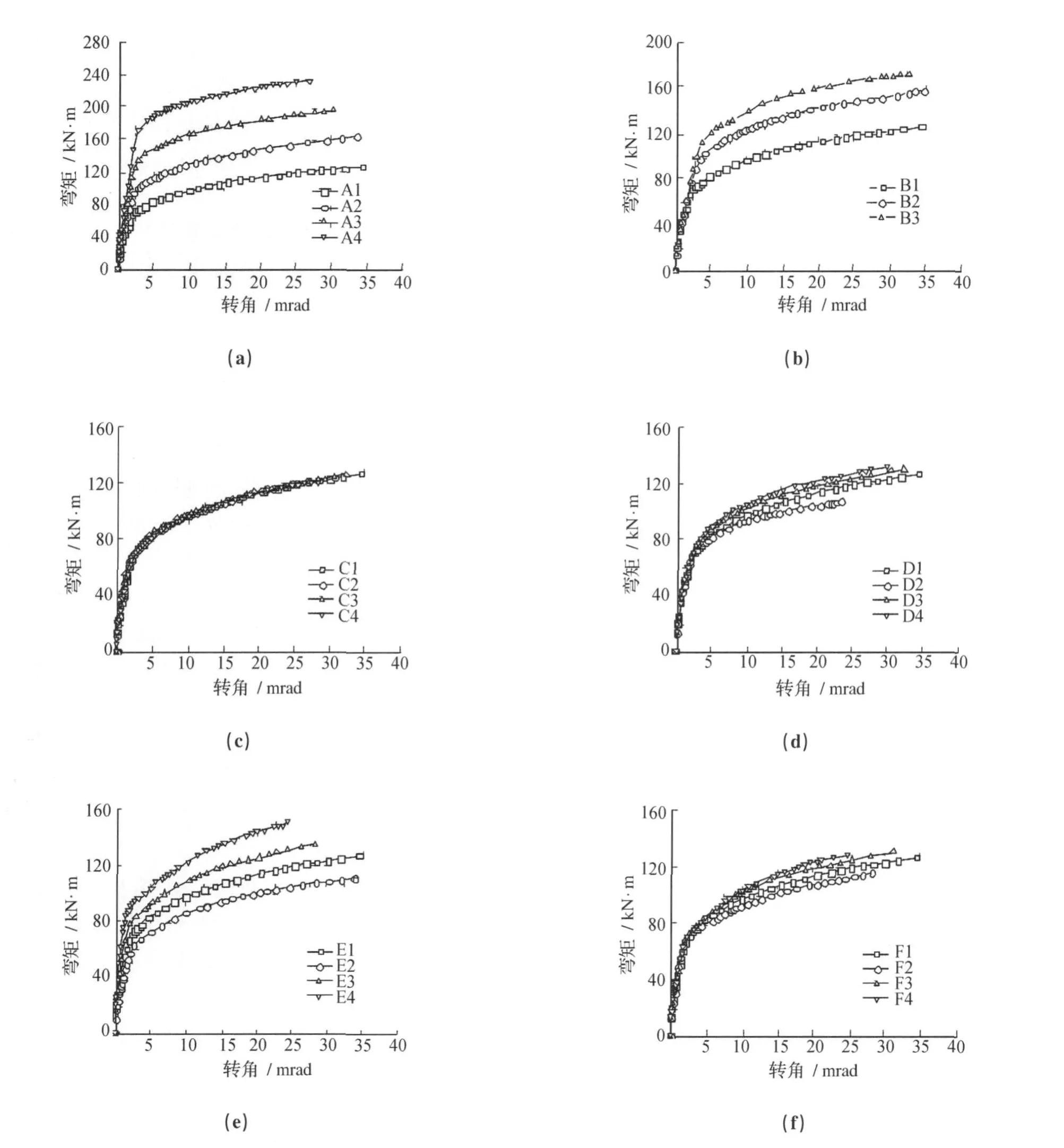
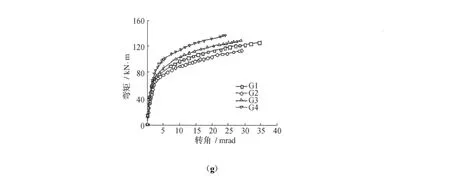
图3 弯矩转角关系曲线Fig.3 Moment versus rotation

3 结 论

本文利用ANSYS有限元软件对部分端板连接钢框架梁柱组合节点进行参数计算,得到以下几点结论:

1)楼板的配筋率、钢筋强度、钢梁高度、端板高度对塑性抗弯承载力的影响很大,配筋率、钢筋强度的增大提高了受拉区的抗拉能力,钢梁高度、端板高度的增大使得转动力臂增大。

2)楼板的的配筋率、钢梁高度对初始转动刚度的影响较大,配筋率增大提高了受拉区的抗拉刚度,钢梁高度的增大使得转动力矩增大。

3)混凝土对强度的影响很小,这也验证了以往理论分析中不考虑混凝土对强度影响的正确性。

[1]Seung-Eock Kim,Se-Hyu Choi.Practical second-order inelastic analysis for three-dimensional steel frames subjected to distributed load[J].Thin-Walled Structures, 2005,43:135-160.

[2]Ali Davaran,Narges Easazadeh Far.An inelastic model for low cycle fatigue prediction in steel braces[J]. Journal of Constructional Steel Research,2009,65: 523-530.

[3]Puhali R.,Iztok Smotlak.and Zandonini R.Semi-rigid composite action:experimental analysis and a suitable model[J].J.Construct.Steel Research,1990,(15): 121-151.

[4]Y.Xiao.Composite connections in steel and concrete-Ⅱ.Moment capacity of end plate beam to column connections[J].Journal of Constructional Steel Research, 1996,37(1):63-90.