降低传感器网络数据聚集延迟的近似调度算法

郭龙江,任美睿,李金宝,范文彬

(1.黑龙江大学 计算机科学技术学院,哈尔滨 150080;2.黑龙江省数据库与并行计算重点实验室,哈尔滨 150001)

0 引 言

在无线传感器网络中,最小化数据聚集延迟问题 (MDAL,Minimum Data Aggregation Latency)是个非常重要的研究课题[1-2]。例如,在一个森林火灾监控系统中,需要把监测到的数据及时地进行数据聚集,以便发现异常,避免迟报火灾。因此,最小化数据聚集延迟问题(MDAL)对于及时获取监视区域内的异常,避免灾害发生或降低灾害损失都有着举足轻重的意义。

MDAL问题可以通过获得数据聚集调度的方法来解决[1-2]。对于给定的一个由若干个传感器节点组成的传感器网络,假设每个节点都有一个需要聚集的数据,数据聚集调度是由所有节点所形成的l个不相交的调度集合,每个调度集合中的节点可以同时传输数据而相互之间不冲突,l×T为整个网络中数据聚集完成所花费的时间,这里T是传感器节点传输一个数据包所要花费的时间。显然,T是固定的,为研究方便,理论上就将l作为整个网络中数据聚集完成所花费的时间。本文研究的问题就是通过减少传输调度集合的个数l,从而使数据聚集延迟减少。

近年来,数据聚集调度问题被广泛研究。最早,由文献 [1]给出一个延迟上界为(Δ-1)R的算法,这里的Δ为网络中的节点最大度 (即一个通信半径内邻居节点的最大个数),R为网络半径(网络中每个节点都有一个到Sink的最小跳数,网络中必有一个节点u使得其到Sink的最小跳数最大,则称节点u到Sink的最小跳数为网络半径)。文献[2]给出一个延迟上界为23R+Δ-18的算法,但是文献 [2]给出的冲突定义有误,本文给予纠正。本文给出一个最大延迟为15R+Δ-15的算法并与文献 [1]的算法和文献 [2]的纠正算法进行比较,验证了不论R和Δ如何变化,本文算法都要优于文献 [1]和文献 [2]的算法。

1 问题描述

本文与文献 [1],文献 [2]的背景完全相同,考虑的是布置在一个平面上的静态无线传感器网络,即该网络由n个固定的传感器节点和一个Sink构成,网络拓扑不随时间变化。如果网络拓扑随时间动态变化,则应该研究分布式的降低传感器网络数据聚集延迟的调度算法,这是另一个研究课题,不在本文的讨论范围之内。

本文假设每个节点具备时间同步能力且知道自己在网络中的位置,Sink知道所有节点的位置和ID,所有节点的通信半径相同。网络的拓扑图用G (V,E)表示,V是网络中节点的集合,E为边集合。如果E中存在边(u,υ),那么当且仅当节点u与节点υ可以通信。

定义1.传输调度 u→υ称为一个传输调度,表示 u可以发送数据到v,这里 u称为发送者(Sender),v称为接收者 (Receiver)。

定义2.传输调度的发送者集合 设S是一个传输调度集合,S={u1→υ1,u2→υ2,…,un→υn},则Sender(S)={u1,u2,…,un}称为传输调度集合S的发送者集合,记为Sender(S)。

本文假设网络采用单信道进行通信,即在一个固定时刻,每个节点不能同时接收和发送,节点要么接收,要么发送。传感器节点可以与以它为中心、通信半径内的所有邻居节点通信。当节点u与向它的一个邻居节点υ发送数据时,这一数据也会同时发送到节点u的所有邻居节点。在同一时刻如果有两个或两个以上的发送者发送的数据同时到达一个节点u,那么节点 u就不能接收到这些数据,这叫做冲突。图 1显示了两种可能的冲突。图1 (a)中,u→v和x→v在同一时刻发生,则v就不能接收到u和x同时发送给v的数据;图1(b)中,u→v和x→y在同一时刻发生,由于v是x的邻居,当x把数据发给y的同时,v也接收到了x发给y的数据,则v就不能接收到u同时发送给v的数据。图1(b)中的虚线表示v和x能通信。

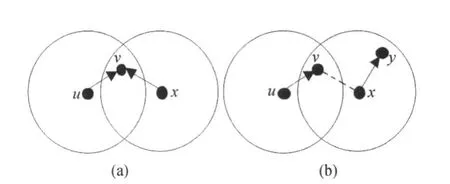
图1 两种冲突Fig.1 Two kinds of conflicts

定义3.冲突 u→υ和x→y发生冲突当且仅当(v,x)∈E or(y,u)∈E,这里E为网络拓扑的边集合。

定义4.数据聚集调度 数据聚集调度就是传输调度集合的集合。M={S1,S2,…,Sl}称为一个数据聚集调度,Si(i=1,2,…,l)是一个传输调度集合,且满足:

1)Si(i=1,2,…,l)中的任何两个传输调度是不冲突的。

2)Sender(Si)∩Sender(Sj)=Ø,∀i≠j,这里Sender(Si)表示Si的发送者集合。

最小化数据聚集调度问题(MDAL)描述如下:给定一个无线传感器网络的拓扑图G=(V, E)以及一个Sink节点s∈V,找到一个数据聚集调度M={S1,S2,…,Sl},使得l最小。

这个问题已经被证明为NP难问题[1]。本文给出一个近似算法,数据聚集延迟上界为15R+Δ-15。Δ是网络的最大度,R是网络半径。

2 相关工作

在无线传感器网络中,广播(Broadcast)和数据聚集 (Data aggregation)是最常用和最基本的操作。在上世纪80年代,人们对广播算法进行了广泛研究[3-14]。相比之下,数据聚集的重要意义一直没有得到重视。在传感器网络中,数据聚集是每个节点的数据作为输入,在网内经过计算得到一个或一些信息然后传送到Sink的操作。近年来,有很多人在研究数据聚集[15-25],在研究中人们更关注如何节省能量。在文献 [24],文献 [25]中提出了用模型驱动来减少能量消耗的方法;文献 [26]权衡了能量消耗和时间延迟,给出了一个均衡的算法;文献 [27]给出一种启发式算法,可以广播和数据聚合;文献 [28]为了节省能量和减少延迟给出了另一种启发式算法,但是这些算法只给出了实验结果,并没有给出理论分析;文献 [29]提出了一种随机分布式数据聚集算法,时间延迟为O(log(n)),在这个模型中,他们假设传感器节点的传输半径可以不受任何限制地进行改变。这个假设对于传感器节点的硬件设计是一个很大的挑战,而且后者在网络规模很大时是不可能实现的。文献 [30]给出了一种使能量消耗和传输可靠性最优化的数据收集调度算法。以上的所有工作都没有讨论最小化数据聚集延迟问题。

与数据聚集调度最相关的工作是文献 [1]和文献 [2]。文献 [1]证明了最小化数据聚集延迟问题为NP难问题并且给出了一个(Δ-1)-近似算法,Δ为网络最大度。这个算法采用了计算最短路径的方法将数据聚集到Sink。文献 [2]给出另一个数据聚集调度算法,时间延迟为23R+Δ-18。R是网络半径,Δ为网络最大度。这个算法引入了白点、黑点、蓝点的概念,采用按照颜色传输的调度方法,这些算法都存在很高的数据聚集延迟。本文给出一个时间延迟上界为15R+Δ-15的算法。

3 本文提出的算法

本节描述本文给出的算法,这个算法的时间延迟为15R+Δ-15。Δ是网络的最大度;R是网络半径,比目前最好的算法[2]给出的23R+Δ-18能更有效地缩短数据聚集时间。相对于文献 [1]给出的(Δ-1)R来说,当Δ很小时,本文提出的算法接近于文献 [1],当Δ逐渐增大时,本文算法能更有效的缩短数据聚集延迟。

本文算法分为:①创建数据聚集树(Data Aggregation Tree,简称DAT);②消减蓝点;③生成传输调度集合;④生成数据聚集调度。②～④是本文核心。

3.1 创建数据聚集树

本节采用文献 [2]的思想来创建数据聚集树(为叙述方便,以下简称DAT)。首先采用广度优先搜索策略来建立广度优先搜索树 (Breadth First Search T ree,以下简称BFST),然后在此基础上建立DAT。

首先,建立BFST。对于给定的网络拓扑图G (V,E)以及Sink节点s∈V,从s开始用广度优先搜索策略建立BFST,并对BFST分层,s节点为第0层,与第0层相连的为第1层,依此类推,直至V中的所有节点都扫描完,以s为根的BFST就建立完成。例如,图2给出一个网络拓扑图G的实例,节点0为Sink节点。图3给出了一个基于图2的以节点0为根的BFST,每个节点头上的数字表示该节点在BFST中的层数,虚线表示两个节点在图G中的边。

接下来,在BFST的基础上建立DAT,这一阶段分两步:

1)从 BFST的根 s开始,按层的升序扫描BFST的所有节点,在第 i层中求出最大独立集BL ACKi,并把独立集中的节点涂成黑色,要求BL ACKi与BL ACKi-1相互独立。初始时,根节点s涂成黑色,BLACK0={s},直至BFST的所有层都扫描完毕。例如,图4是基于图3的BFST建立的DAT,按层扫描完毕后产生的黑点集合(最大独立集)为:BL ACK0={0},BLACK1={}, BL ACK2={7,8,9,10,11,12,13},BL ACK3 ={},BLACK4={20},BLACK5={22}。

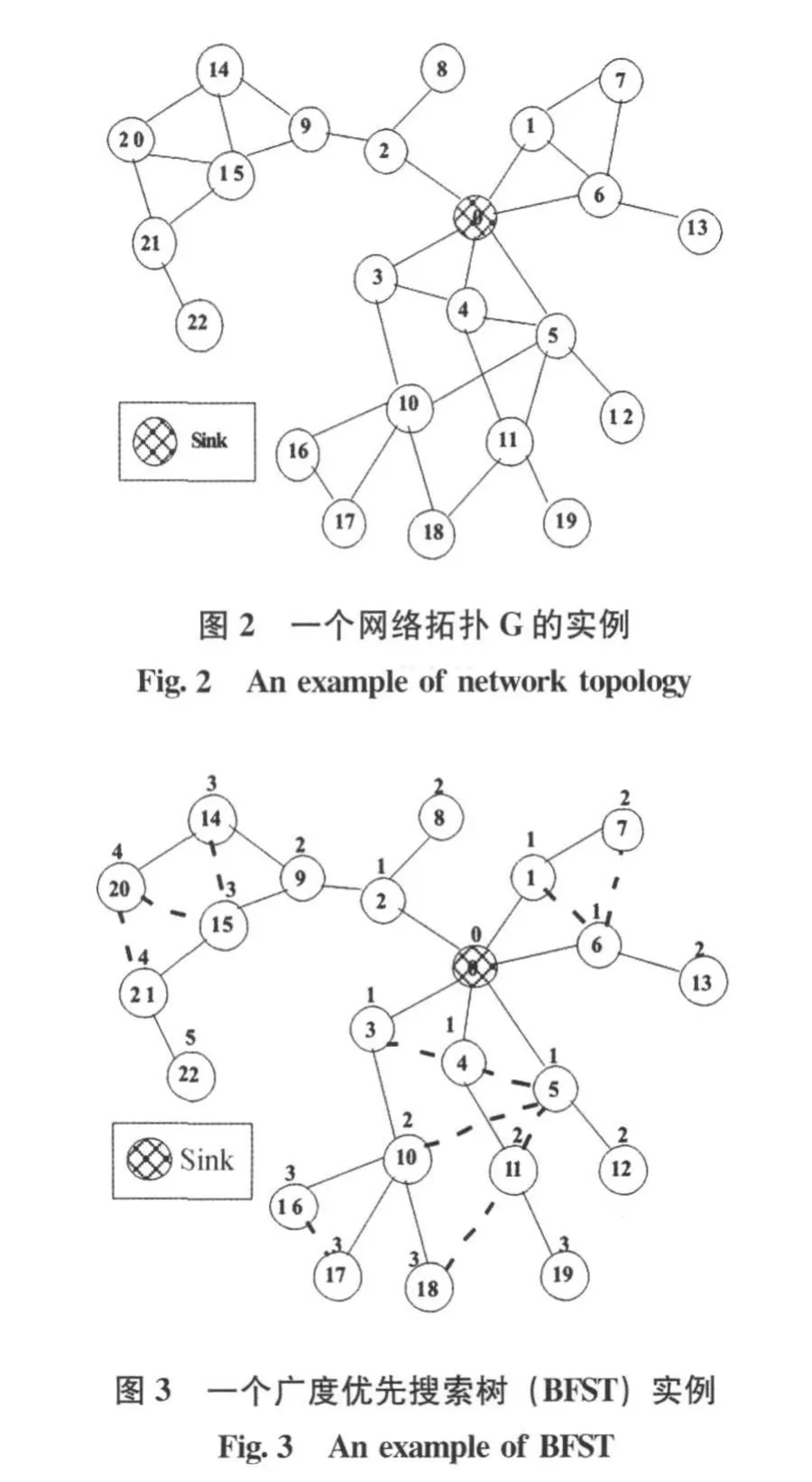
2)按层的升序,从第2层开始扫描每一层的黑点集合,对于BLACKi中的一个节点v,找到v在BFST中的父亲节点p(v),并将p(v)涂为蓝色,对于蓝点p(v),在它的同层或上层找一个与它相连的黑点dp(v)作为p(v)的父亲节点,然后把边(v,p(v))和(p(v),dp(v))加入到DAT中,直至BFST的所有层都扫描完毕。最后,所有没有涂上颜色的节点称为白点,为白点找一个黑点作为父亲节点。例如,图4是基于图3的BFST建立的DAT。文献[2]给出了建立DAT的详细算法,限于篇幅这里不再赘述。

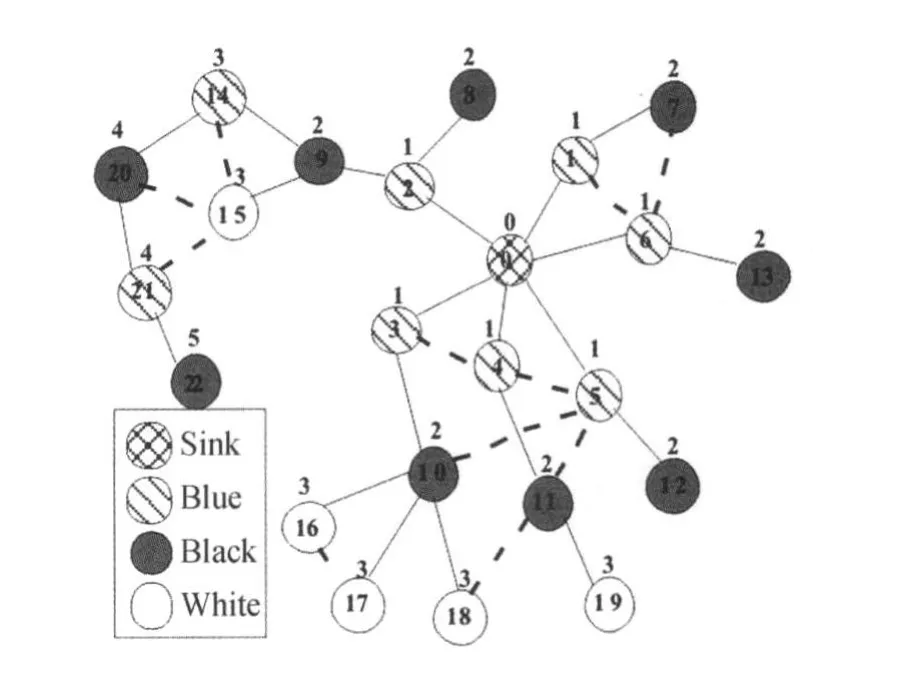
图4 一个数据聚集树(DAT)实例Fig.4 An example of DAT

3.2 消减蓝点

文献 [2]把生成数据聚集调度分为3个阶段:①白点到黑点的聚集;②黑点到蓝点的聚集;③蓝点到黑点的聚集。通过对这3个阶段的数据聚集延迟的分析,得出数据聚集延迟上界为23R+Δ-18。文献 [2]数据聚集延迟的分析依赖对一个黑点一跳范围内蓝点数目的估计,该蓝点数目的估计越小,算法的数据聚集延迟越小。文献 [2]证明了一个黑点一跳范围内最多有21个蓝点,本文算法的核心思想就是通过减少一个黑点一跳范围内蓝点数目来减少时延。本节通过定理2证明了一个黑点一跳范围内最多保留12个蓝点就足够了。

引理1[2].一个黑点两跳范围内最多有21个黑点。

证明:详见文献[2]。

定理1[2].一个黑点一跳范围内最多有21个蓝点。

证明:由引理1可知,一个黑点两跳范围内最多有21个黑点,每个黑点有一个蓝父亲,当这21个黑点与该黑点相连的蓝父亲都不相同时,该黑点一跳范围内最多有21个蓝点。定理1得证。

定义5.不相交 设与同一黑点S通过蓝点间接相连的任意两个黑点为x,y,x在DAT中的蓝父亲为p(x),y在DAT中的蓝父亲为p(y),如果x与p(y)不能通信且y与p(x)不能通信,则x与y不相交。

如图5(a)所示,x与p(y)不能通信且y与p(x)不能通信,则黑点x与黑点y不相交。图5(b)中y与p(x)能通信,则黑点x与黑点y相交。虚线表示y与p(x)在网络拓扑中有边相连,但是该边不是DAT中的边。

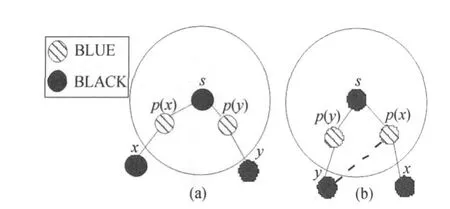
图5 两个黑点不相交与相交的情况Fig.5 Joint and disjoint black nodes

引理2.对于一个黑点S的两跳范围内的任意两个黑点x、y,如果x与y不相交,那么夹角xSy＞arccos(7/8)。

证明:为证明方便,假设一个传感器节点的通信半径为1。黑点S的两跳范围内的任意两个黑点一定在以黑点S为圆心,半径为2的圆中,为叙述方便称该圆为DS2。以黑点S为圆心,1为半径的圆称为DS1。

证明前先做一些准备工作:①如图6(a)在DS2内任选一个黑点 x,作一直线 xS,并延长xS与DS2交于一点A,与DS1交于一点F;②以 A点为圆心,1为半径做一圆周与相交于两点B和B′;③作直线BS与交于一点E。AB=1,AS =BS=2,根据余弦定理:

AB2=AS2+BS2-2AS×BS×cos∠ASB计算得∠ASB=arcos(7/8)。从S出发向以A为圆心的圆做切线(由于切线与SB,图6(a)中没有画该切线),切线与AS夹角为30°,BS与AS夹角∠ASB=arcos(7/8)＜30°,因此BS必与DS2相交于两点,无妨设离S最近的点为C;④做直线AC,AC=1,并且做平行于AB的直线CD交AS于D点。

现只需证明:图6(a)中的扇形区域ASB内不存在与x不相交的黑点。

反证法:假设在扇形区域ASB内存在一个黑点y与x不相交。△ABC和△ABS都是等腰三角形,而且这两个三角形有一个公共角∠ABS,因此△ABC和△ABS是相似三角形。AC=AB=1,AS =BS=2,根据比例BC/AB=AC/AS=0.5,因此BC=0.5,所以SC=SB-BC=1.5。DC是AB的平行线,所以△DSC是等腰三角形,DS=DC= 1.5,AD=AS-DS=0.5=BC,因此四边形ABCD是等腰梯形。由AC=1可知,梯形区域ABCD内任意两点的最大距离为1。

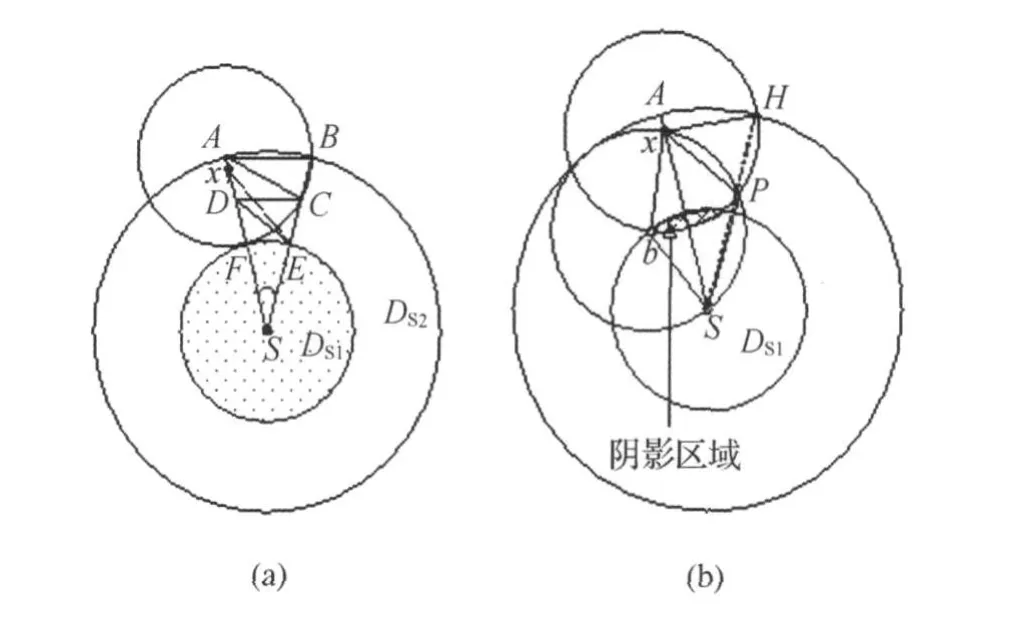
图6 两个不相交黑点的夹角估计Fig.6 Angle estimation for two disjoint black nodes

DC和AB是平行线,所以△DSC和△ASB是相似三角形,DC/AB=SC/SB=3/4,因此,DC =3/4,CE=SC-SE=1.5-1=0.5。在△DCE中,由余弦定理知:

DE2=DC2+CE2-2DC×CE×cos∠DCE

又因为DC是AB的平行线,∠DCE=∠ABS,在△ABS中,由余弦定理知:

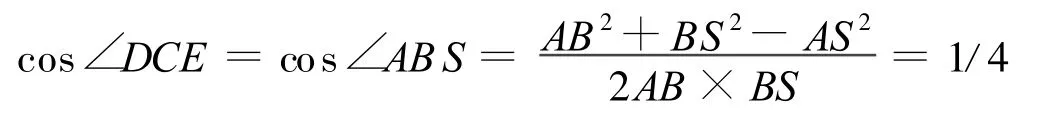
因此,DE=10/4＜AC=1,梯形区域CDFE内的任意两点的最大距离＜1。

综合以上讨论,梯形区域CDFE和梯形区域ABCD内各自只能存在一个黑点,黑点 x在区域ABCD内,且在 AD上,那么黑点y一定在区域CDFE内。因为黑点 x的合理区域是DS1之外和DS2之内,所以1＜xS≤2。

以下分两种情况讨论:xS≤1.75和 xS＞ 1.75。

1)当xS≤1.75时,根据余弦定理:

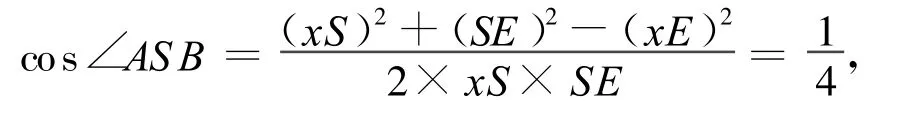
推出xE≤1。

E是区域CDFE内距离x点最远的点。因此,区域CDFE内的所有点到x的距离≤1,这时y在区域CDFE的任何位置,x与y都能够通信,与x与y是黑点矛盾,所以当xS≤1.75时,扇形区域ASB内不存在与黑点x不相交的其他黑点。

2)当xS＞1.75时,设b为连接黑点x与黑点S的蓝点,无妨设b在直线SA左侧,见图6(b)。bx≤1且Sb≤1。以 x为圆心,1为半径做一圆(该圆为黑点x的最大覆盖范围,为叙述方便称此圆为Dx1)交DS2于点H,连接HS(如图6(b)中所示的虚线)。以b为圆心,1为半径做一圆(该圆为蓝点b的最大覆盖范围,为叙述方便称此圆为Db1)与圆Dx1交于P点(见图6(b),注意P点不一定在虚线SH上)。

如果H点和P点不在图6(a)中的扇形区域ASB内部(可以在SB边上),说明图6(a)中的扇形区域ASB全部处在Dx1与Db1内部,而Dx1与Db1内部不存在与 x点不相交的黑点。这时y在区域CDFE的任何位置,x与y都能够通信,这就与x与y是黑点矛盾。因此,当 xS＞1.75时,(图6 (a)中)扇形区域ASB内不存在与x点不相交的其他黑点。如图6(b)所示,现只需证明:H点和P点不在图6(a)中的扇形区域ASB内部 (可以在SB边上),就可得出结论:当xS＞1.75时,(图6(a)中)扇形区域ASB内不存在与x点不相交的其他黑点。

(I)首先证明:H点不在图6(a)中的扇形区域ASB内部(可以在SB边上)。已知S H=2, 1.75＜xS≤2,xH=1,根据余弦定理:

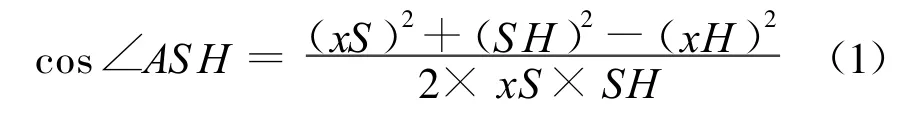
得:cos∠ASH≤7/8,∠AS H≥arccos(7/8)=∠ASB。这就证明了H点不在如图6(a)所示的扇形区域ASB内部,但H点可以在直线SB上。

(II)接着证明:P点不在图6(a)中的扇形区域ASB内部(可以在SB边上)。证明思路是:当∠ASP取最小值时,∠ASP＞∠ASB成立。

蓝点b的合理活动区域为如图6(b)所示的直线 AS左侧的阴影区域内 (阴影区域是DS1与Dx1相交区域)。当 x点固定且b点在DS1与Dx1的交点上时 (该交点在直线AS左侧),b距离边xS最远,此时xb=1,bS=1且∠ASP最小。根据余弦定理:

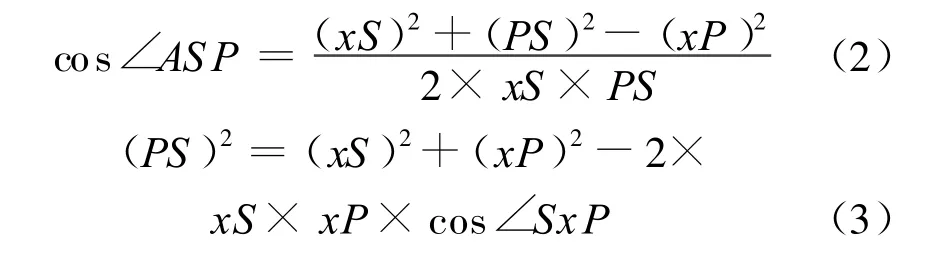
△xbP为等边三角形,因此有:

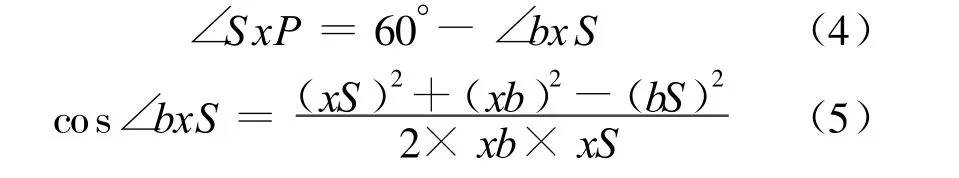
由xb=1,bS=1得:cos∠bxS=xS/2。

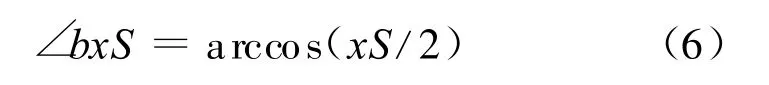
综合式(4)和式(6)得:

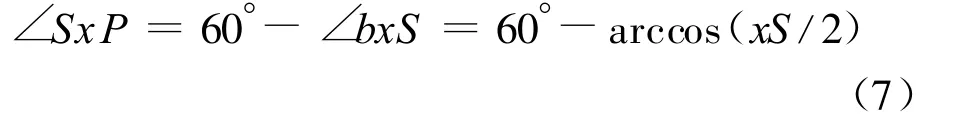
将式(7)代入式(3),再将式(3)代入式(2)得:

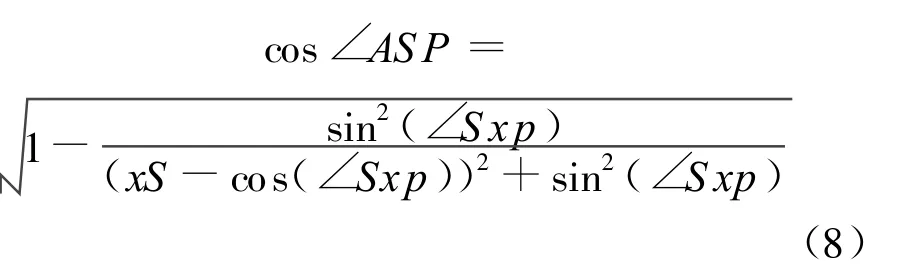
由式 (7)和cos∠bxS=xS/2得出xS=cos(60 -∠S xp),代入式 (8)∠Sxp被削去得出cos∠ASP=3/2,所以 ∠ASP=arcos(3/2)＞arcos(7/8)=∠ASB。这就证明了P点不在如图6(a)所示的扇形区域ASB内部。

综合(I)(II)的讨论得出结论:H点和P点不在图6(a)中的扇形区域ASB内部(可以在SB边上),从而当xS＞1.75时,(图6(a)中)扇形区域 ASB内不存在与x点不相交的其他黑点。

综上所述,无论xS≤1.75还是xS＞1.75,黑点y一定在区域CDFE内都得出矛盾,因此假设在扇形区域ASB内存在一个黑点y与x不相交是错误的。得证。

定义6.覆盖 对于DAT=(Vd,Ed)中的一个蓝点 x以及一个黑点y,如果x与y能通信且x.level＜y.level(level表示节点层数),则称蓝点x覆盖黑点y。

定理2.在DAT=(Vd,Ed)中,最多12个蓝点就可以把一个黑点两跳范围内间接相连的所有黑点全部覆盖。

证明:定理2的证明等价于证明一个黑点两跳范围内最多有12个互不相交的黑点。采用反证法:假设在DAT=(Vd,Ed)中,一个黑点s两跳范围内有13个互不相交的黑点。如图7所示,对于黑点s两跳范围内的某一个黑点A,连接 AS顺时针旋转 arccos(7/8)到B点,逆时针旋转arccos (7/8)°到C点,于是∠BSC=2arccos(7/8)＞57.9°,根据引理2小圆弧BC(从B点逆时针旋转到C点形成的圆弧)内不存在与A不相交的黑点。对大圆弧BC(从B点顺时针旋转到C点形成的圆弧)分成11等份,每份的弧度b=(360-∠BSC)/11＜27.46＜arccos(7/8)。把剩下的12个黑点分到11个相等的扇形内,根据鸽巢原理,至少有两个黑点落到同一个扇形区域内,根据引理2,这两个黑点必相交,这与13个黑点是互不相交的假设矛盾。

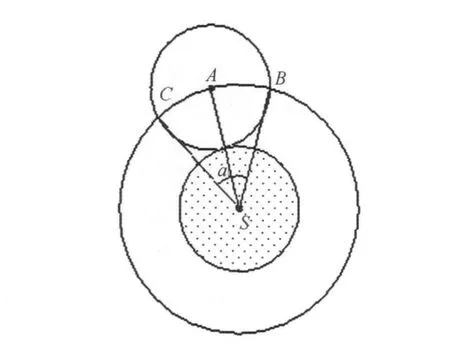
图7 两跳范围内的黑点覆盖Fig.7 Black node coverage in two hops away

定义7.消减 给定一个DAT以及DAT中的一个黑点集合BLACK,与BL ACK中黑点相连的下级蓝点集合记为BL={bl1,bl2,…,bln},BL中所有蓝点覆盖的黑点 (不包括BLACK中的节点)集合记为B={b1,b2,…,bm},如果存在蓝点集合MB⊂BL,且MB中的蓝点可以覆盖B中所有的黑点,那么称BL可以消减为MB。

在DAT中,由定理1知:一个黑点两跳范围内的所有黑点,最多用21个蓝点就可以覆盖。而由定理2知:一个黑点的两跳范围内与其间接相连的所有黑点,最多用12个蓝点就可以覆盖。本文的核心思想就是通过减少黑点一跳范围内蓝点的数目来减少延迟。下面本文给出一个贪心算法 Reduce-Blue-Node来消减蓝点。

Reduce-Blue-Node算法以DAT树作为输入,对DAT树由Sink节点开始逐层向外扫描,对于第i层的黑点集合BL ACKi,得到与其相连的下级蓝点集合BLi。Bi为被集合BLi覆盖的黑点集合(不包括BL ACKi中的黑点)。Reduce-Blue-Node算法为BLi中每个蓝点计算一个权值 (算法中的count变量),用来表示该蓝点覆盖集合Bi中黑点的个数;接着在BLi集合中找count值最大的蓝点b,这时集合Bi中被蓝点b所覆盖的所有黑点都变成b的孩子,也就是去除这些黑点与原来蓝父亲之间的边,并连接到蓝点b上。在集合BLi中去除蓝点b,以及在Bi中去除被蓝点b覆盖的黑点,更新BLi中剩余蓝点的 count值。依此方法做下去,直到Bi集合空为止,把BLi中剩余蓝点变成白色,第i层消减完毕。当扫描完DAT中的所有的层,算法结束,返回消减后的数据聚集树RDAT。Reduce-Blue-Node算法的伪代码如Algorithm -1所示。

以图4为例,首先对第0层进行消减, BLACK0={0},BL0={1,2,3,4,5,6},B0= {7,8,9,10,11,12,13},选择count值最大的5号蓝点,其 count值为3,5号蓝点覆盖黑点10, 11,12。黑点10,11,12变为5号蓝点的孩子,即在算法中断开 (v3,v10)、(v4,v11),连接 (v5, v10)、(v5,v11)。在BL0中去掉5号节点BL0更新为BL0={1,2,3,4,6},在B0中去掉被5号节点覆盖的10,11,12节点更新为B0={7,8,9, 13}。在 BL0中选择 count值最大的 6号蓝点, count值为2,断开 (v1,v7),连接 (v6,v7),更新BL0={1,2,3,4},B0={8,9},选择count值为2的2号蓝点,边不变,更新BL0={1,3, 4},B0={},B0为空,把1,3,4号蓝点变为白点,第0层消减完毕。接下来以此方法对第1～5层进行消减,当所有层都消减完,算法结束,得到如图8所示的数据聚集树。

Algorithm-1 Reduce-Blue-Node Input:Network topology G=(V,E),Data Aggregation T ree DA T=(VDAT,EDAT),Sink node s. Output:Reduced Data Aggregation T ree RDAT=(VRDAT, ERDAT) 1.Procedure Reduce-Blue-Node(G,DAT,s) 2.VRDAT←V;ERDAT←EDAT 3.FOR i←0 to l DO 4.BLACKi←{The Black node in level i} 5.BLi←{Blue nodes which are children of BL ACKi} 6.Bi←{Black node covered by BLi} 7.FOR all blue node b in BLiDO 8.b.count←the number of nodes in Bicovered by b. 9.END FOR 10.WHILE Bi≠Ø DO 11.find a node b such that b.count is maximum in BLi 12.FOR all black j covered by b in BiDO //pDAT(j)is node j's father in DA T 13.remove(j,pDAT(j))from ERDAT; 14.add(b,j)into ERDAT; 15.remove j from Bi; 16.END FOR 17.remove b from BLi 18.update Blue nodes'count of BLi 19.END WHILE 20.Color Blue nodes of BLito White 21.END FOR 22.RET URN RDAT=(VRDAT,ERDAT) END

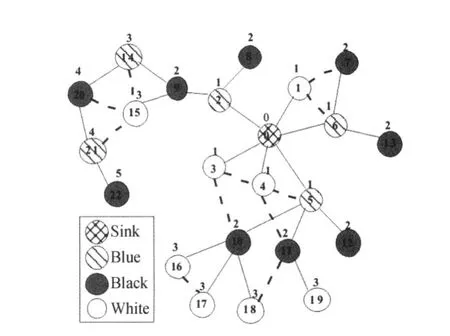
图8 消减蓝点后的数据聚集树(RDAT)Fig.8 An example of RDAT after blue nodes are reduced

3.3 生成传输调度集合

RDAT建立成功后,接下来本节首先指出文献[2]中的冲突定义是如何错误的,并给予纠正,然后给出Mini-Slot算法生成传输调度集合。

对于给定G=(V,E),节点u,vV,(u,p (u)),(v,p(v))E,p(u)、p(v)分别为u和v在RDAT中的父亲节点,如果(p(u),v)E且(p(v),u)E,那么u,v不冲突。如图9(a)、(b)所示,u和v分别向p(u)、p(v)发送数据包会产生冲突,因为(a)中u和v同时向p(u)和p (v)发数据包时,p(u)会同时收到u,v的数据包,产生冲突。同理(b)中u和v同时向p(u)和p(v)发数据包时,p(v)也会同时收到u,v的数据包。如果u,v冲突,那么他们不能在同一个调度集合中。而文献[2]中只考虑了(p(u),v) E和(p(v),u)E其中的一种条件。例如在文献[2]的算法中,对于某一传输调度集合S,假设u最先进入集合S中。当扫描到v时该算法只判断是否满足(p(u),v)E这个条件,那么对于图9 (a),v不会加入S中,此时文献 [2]的算法能得到正确的调度。但是对于图9(b),由于(p(u), v)E,则v被加入了传输调度集合S,但实际上u与v是冲突的,所以发生了错误。文献 [2]采用的是分层聚集策略产生数据聚集调度,由于文献[2]的冲突定义出现错误,导致理论分析时白点聚集数据到黑点不能在 Δ-1个时刻内完成。例如在图10(a)给出的数据聚集树中(实线表示数据聚集树中的边,虚线表示两个节点能够通信),这棵树的 Δ=5,按照文献 [2]的冲突定义和理论分析应该在Δ-1=4个时刻内完成。然而,根据本文给出的正确冲突定义并采用文献 [2]给出的算法,白点向黑点传输聚集数据的传输调度集合为:S1= {9→6,10→7},S2={11→7,12→6},S3={13→8},S4={14→8},S5={15→8},S6={16→8},即需要6个时刻完成聚集。同理,在分析蓝点到黑点和黑点到蓝点的延迟上界时有同样的错误。本文下面将给出一个Mini-Slot算法(Algorithm-2)来纠正这个错误。

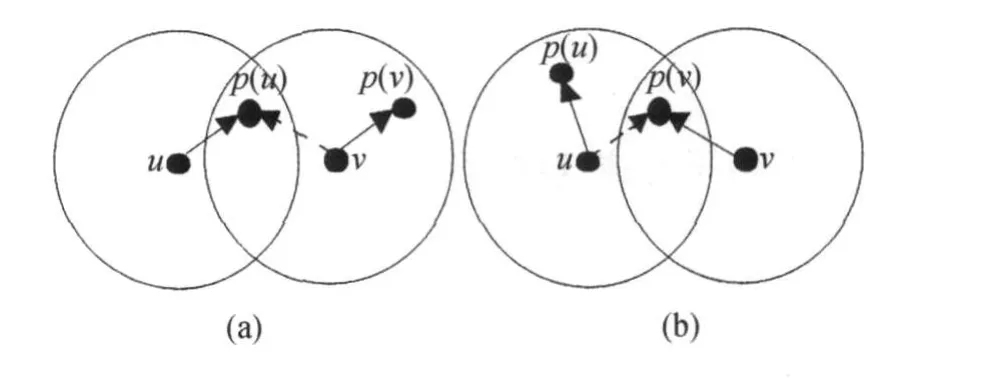
图9 冲突演示Fig.9 Demo for conflicts

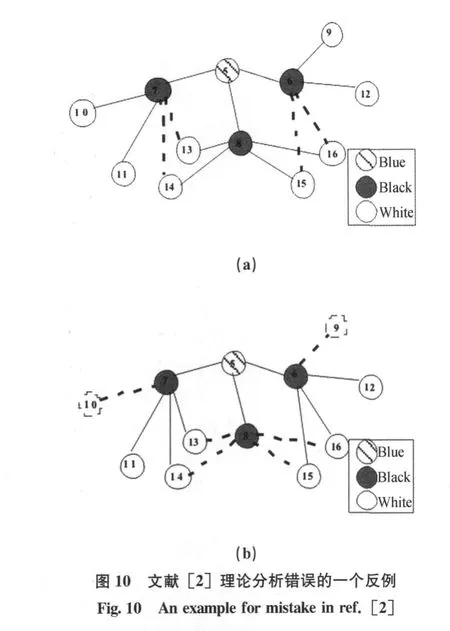
Mini-Slot算法输入包括3部分:候选发送节点集合Leaf,消减后的数据聚集树RDAT和网络的拓扑G=(V,E)。Mini-Slot算法返回一个由若干个传输调度集合组成的数据聚集调度M。

Mini-Slot算法中的Father集合为候选发送节点的父亲节点集合。Other集合由RDAT中且不在Leaf集合内的其他叶子节点构成。对于该算法生成的第i个传输调度集合Si={}(i初值为1),对于Father集合中每个节点j(j作为接收者),算法从Leaf中选一个节点k使得k→j与Si中的传输调度不冲突,将k→j加入到Si中,把节点 k从Leaf中去掉;如果Leaf中不存在这样的节点k,且节点j与Si中的所有发送节点不能通信,说明节点j的孩子与Si中的接收者能够通信,那么把节点j的孩子变成这些接收者的孩子。

当节点j在Leaf集合中没有孩子时,把j从Father集合中去掉,如果 j是当前RDAT的叶子,则把j加入Other集合;当Father集合扫描一遍后,得到Si,然后扫描一遍Other集合,对其中的节点m,如果满足m→pRDAT(m)与Si不冲突,m→pRDAT(m)加入到Si中。对Other集合操作完毕,把 Si加入M中。算法重复上述过程,直到Leaf集合为空时算法结束。Mini-Slot算法运行结束,相当于把RDAT的所有叶子 (即Leaf中的节点)裁剪掉。Algorithm-2中给出了Mini-Slot的伪代码。

例如图10(a)所示,当前候选发送节点集合为:

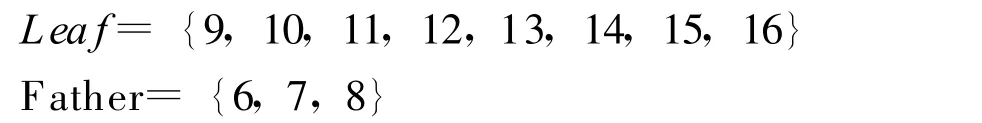
首先对于节点6,9号节点可以发送,9→6加入S1中,然后是节点7,10→7号节点加入S1,节点8与当前发送者9和10没有边相连,则节点8可以接收,但是8号节点的孩子都不能发,那么8号节点的孩子就更改其父亲。8号节点的孩子为13,14,15,16,其中13,14与7号相连,15,16与6号相连,那么父子关系变成图10(b)所示,9和10从Leaf中去掉,8由于没有孩子,也从Father中去掉,第一遍扫描完Father得到S1={9→6,10→7}。然后对于 Leaf={11,12,13,14, 15,16},Father={6,7},重复上述过程,直到Leaf为空算法结束。最后得到,S2={11→7,12→6},S3={13→7,14→6},S4={15→6,16→7}。图11显示了以图10(a)作为输入Mini-Slot算法运行结束后裁剪完叶子的RDAT。

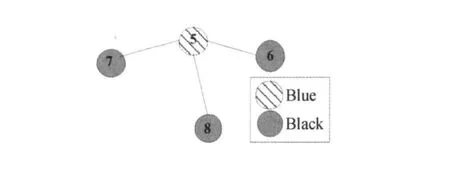
图11 以图10(a)作为输入Mini-Slot算法运行后的RDATFig.11 A RDAT after running Mini-Slot using 10(a)as input

定理3.给定一个候选发送节点集合Leaf= {l1,l2,…,ln},Leaf中所有节点的父亲集合为Father={f1,f2,…,fm},Father集合中节点通信范围内的候选节点的个数为 {d1,d2,…, dm}。令Max{d1,d2,…,dm}=D,则Leaf中的节点作为发送者,Father中的节点作为接收者,通过Mini-Slot算法所形成的不冲突的传输调度集合最多有D个。

证明:首先,对于 Father={f1,f2,…, fm},d1,d2,…,dm分别是 f1,f2,…,fm的通信范围内的候选发送节点的个数。Max{d1,d2,…,dm}=D。根据Mini-Slot算法的描述,扫描一遍Father集合生成一个传输调度集合。

Algorithm-2 Mini-Slot Input:Candidate Sender Set Leaf,Topology of Network G= (V,E),Reduced Data Aggregation Tree RDA T=(VRDAT, ERDAT) Output:Data Aggregation Schedule M. 1.Procedure Mini-Slot(Leaf,G,RDA T) 2.i←1,M←Ø,Father←Ø 3.FOR l Leaf DO 4.add pRDAT(l)to Father;//pRDAT(l)is l's father in RDAT 5.END FOR 6.WHILE Lea f≠Ø T HEN 7.Si←Ø 8.Other←{Leaves of RDA T but not in Leaf}; 9.FOR j Father DO 10.find a node k from Leaf which a child of j such that k→j conflict-free with all transmission schedule in Si 11.IF k exists in Leaf THEN 12.add k←j to Si; 13.remove k from Leaf; 14.remove(k,j)from ERDAT; 15.ELSE//k does not exist in Leaf 16.IF does not exist node t which in Sender(Si)can connect with j//T his means j can receive data 17.THEN 18.remove j from Father 19.FOR each j's child t in Lea f DO 20.find a node x from Father can connect with t 21.add(x,t)into ERDAT; 22.remove(t,j)from ERDAT; 23.END FOR 24.IF j's all children are not in Leaf 25.THEN remove j from Father 26.IF j is a leaf in RDA T 27.THEN add j to Other 28.END FOR//corresponds to FOR j Father DO 29.FOR m Father DO 30.IF m→pRDAT(m)conflict-free with all transmission schedule in Si 31.THEN 32.add m→pRDAT(m)to Si; 33.remove(m,pRDAT(m))from ERDAT;

34.END FOR 35.add Siinto M 36.i→i+1 37.END WHILE 38.RETU RN M END

对于Father中的fk:(1)如果fk与Si中的至少一个发送节点有边相连,并且该发送节点已从Leaf中删除,那么 fk对应的dk在这次扫描中至少减少1;(2)如果fk与当前调度集合Si的发送者无边相连,那么在 fk的孩子节点中找一个与调度集合Si不冲突的发送节点lj:(2.1)如果Leaf中存在这样的lj,把lj→fk加入到Si中,并把lj从Leaf中删除,那么dk减1;(2.2)如果Leaf中不存在这样的lj,说明 fk任意孩子节点都与Si的某个接受者有边相连,那么把 fk从Father中去除,dk置0,并为 fk的孩子节点在集合Father中重新找一个父亲节点,该操作并不改变 d1,d2,的值。

综合(1)(2),经过一遍扫描Father集合产生一个调度集合,{d1,d2,…,dm}中的每个值都至少减1。而Max{d1,d2,…,dm}=D,所以最多扫描Father集合D次就可以把 {d1,d2,…,dm}的所有值都置0。当 {d1,d2,…,dm}的值全部置0时,说明Leaf当前为空。每扫描一次Father集合产生一个传输调度集合,因此以Leaf中的节点作为发送者,Father集合中的节点作为接收者所形成的不冲突的传输调度集合最多有D个。证毕。

例如,图10(a)所示的树其中Leaf={9, 10,11,12,13,14,15,16},Father={f1=6, f2=7,f3=8},相应的d1=4,d2=4,d3=4。根据Mini-Slot算法最多用4个传输调度集合把Leaf集合中节点信息聚集到Father集合中。

3.4 数据聚集调度生成算法

本节首先基于Mini-Slot算法给出数据聚集调度生成算法Data-Aggregation-Schedule,然后给出该算法的时间延迟理论分析。

Data-Aggregation-Schedule算法在 RDAT的基础上生成数据聚集调度,主要分为以下两个步骤:

1)原始RDAT树的所有叶子节点(包括白色节点和黑色叶子节点)作为候选发送节点集合,应用Mini-Slot算法把数据聚集到RDAT树的内层。

2)对经过1)裁剪过后的RDAT树按层从外向内聚集,先把最外层的蓝色叶子节点作为候选发送节点应用Mini-Slot算法产生数据聚集调度,把信息聚集到内层,然后再把外层的黑色叶子节点作为候选发送节点Mini-Slot算法产生聚集调度,把信息聚集到内层。重复2),直到所有节点的信息都聚集到Sink节点为止。

Algorithm-3给出了 Data-Aggregation-Schedule算法。对于图8所示的RDAT产生数据聚集调度,第一轮得到S1={1→0,8→2,12→5, 15→9,16→10,19→11},从RDAT中裁剪掉S1中的所有发送节点,进行第二轮聚集调度生成S2= {3→0,7→6,11→5,22→21},依此律推一共进行7轮数据聚集调度过程:S3={4→0,17→6,13→10,21→20},S4={6→0,18→10,20→14},S5= {10→5,14→9},S6={5→0,9→2},S7={2→0}。最后得到7个调度集合,所以该例用7个时刻就能完成数据聚集。

Algorithm-3 Data-Aggregation-Schedule Input:Topology of Network G=(V,E), Output:Data Aggregation Schedule M. 1.Construct Breadth First Search T ree BFST; 2.Construct Data Aggregation Tree DAT; 3.RDA T←Reduce-Blue-Node(G,DAT,s); 4.Leaf←{i|i is a leaf of RDAT}; 5.M←M∪Mini-Slot(Leaf,G,RDAT); 6.FOR j←deep to 1 DO 7.Leaf←{i|i is RDA T's blue node which is a leaf}; 8.M←M∪Mini-Slot(Leaf,G,RDAT); 9.Leaf←{i|i is RDAT's black node which is a leaf}; 10.M←M∪Mini-Slot(Leaf,G,RDAT); 11.END FOR End

4 数据聚集调度生成算法的理论分析

本节对Data-Aggregation-Schedule算法的时间延迟进行理论分析。

引理3.一个蓝点的通信半径内,以该蓝点为顶点的任意两个黑点的夹角＞60°。

证明:如图12所示,不妨设S为蓝点,通信半径为1,A,B为S通信范围内的黑点,A与B通过S的夹角为θ。那么根据余弦定理:cosθ=因为A和B都是黑点,相互独立,c＞1。所以又因A,B都在S的通信范围内,所以a≤1,b≤1。不妨设a≤b,令,f所以a=b是f(a)取最大值,b≤1,所以 f(a)≤60°,S通信半径内的任意两个黑点通过S的夹角＞60°。证毕。

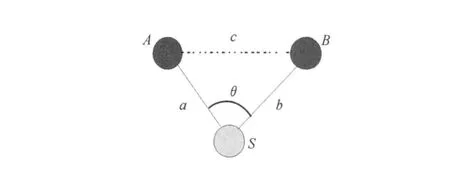
图12 两个黑点的最小夹角Fig.12 Minimum angle between two black nodes

定理4.一个蓝点的通信半径内最多有5个黑点。

图13 一跳范围内黑点分布Fig.13 Black nodes distribution in one hop away

证明:反正法:假设一个蓝点的通信范围内可以有6个黑点。如图13(a)所示,对于S通信半径内的某个黑点A,以S为圆心顺时针、逆时针各旋转60°,使得 x1SA,ASx2=60°;根据引理1, x1Sx2这段扇形区域内不能有其他黑点;把剩下的扇形x1x3x4x5x2区域 (图13(b))平均分成4份,则每个扇形区域的夹角为60°。除去黑点 A,剩下的5个黑点必落入这4个扇形中,根据鸽巢原理,必然有两个黑点落入一个小扇形区域内,由于每个小扇形的夹角＜60°,与引理3矛盾,所以一个蓝点的通信范围内的黑点个数要＜6个,与假设矛盾,定理4得证。

下面分析一下本文的 Data-Aggregation-Schedule算法在最坏情况下的时间延迟上界为15R +Δ-15。

根据Algorithm-3,已知图G的最大度为Δ,那么RDAT最外层的叶子节点的父亲的通信范围内的候选节点的个数不会超过 Δ-1,因为这些父亲节点(除了Sink之外)都有一个父亲节点,那么应用Mini-Slot算法根据定理3最多用Δ-1个时刻就能把这些节点的数据聚集到内层。所有的叶子节点(包括所有白色节点和部分黑色节点)被裁剪之后,RDAT中只剩下蓝点和黑点。根据Algorithm-3,R是网络半径,先从蓝点到黑点进行数据聚集,再从黑点到蓝点进行数据聚集。根据定理2,任意一个黑点b一跳范围内最多有12个蓝点,每个黑点都需要与一个蓝父亲相连,那么需要向黑点b聚集的蓝点最多有11个 (向Sink节点聚集的蓝点最多可以有12个)。根据定理3,蓝点聚到黑点b最多需要11个时刻。根据定理4,蓝点1跳范围内最多有5个黑点,去掉与上层相连的一个黑点,需要向蓝点聚集的黑点最多4个,根据定理3,黑点聚集到蓝点最多需要4个时刻。由RDAT可知,只有第2到R层可能存在黑点,第1到R-1层可能存在蓝点,那么RDAT中最多有(R-1)层需要将数据聚集到黑点,最多有(R-1)层需要将数据聚集到蓝点,最后Sink周围最多有12个蓝点,需要12个时刻,再加上白点向内层聚集的Δ-1个时刻,最多需要Δ-1+(R-2)11+12+(R -1)4=15R+Δ-15个时刻。

定理5.Data-Aggregation-Schedule算法的近似比为16。

证明:对给定的网络拓扑G=(V,E),网络半径为R,网络的最大度为 Δ,那么最优聚集延迟Latency满足:Latency max(R,Δ),则近似比r =(15R+Δ-15)/Latency

当R时,r 15

当Δ时,r 1

当R,Δ时,r 16证毕

5 实 验

本文算法将与文献 [1],文献 [2](纠正冲突定义后)所提出的算法在各种不同的拓扑结构下的数据聚集延迟进行比较,主要针对节点个数变化、通信半径变化、网络的度变化和网络半径变化,在这些不同的拓扑图中比较数据聚集延迟,衡量标准为数据聚集调度集合的个数,调度集合个数越少,说明聚集延迟越小。

首先,考察节点个数变化对聚集延迟的影响。把传感器节点随机的布置在200 m×200 m的范围内,每个节点的通信半径相同。3种算法在同样的网络拓扑结构下进行比较,节点变化范围从500个增长到1 900个,增幅为100,每个节点的通信半径为25 m,Sink节点在矩形区域的顶点位置。对于节点数n=500,600,…,1 900,每个n本文随机生成30个拓扑图,延迟分别取30个不同的拓扑图的聚集延迟的平均值,实验结果如图14。

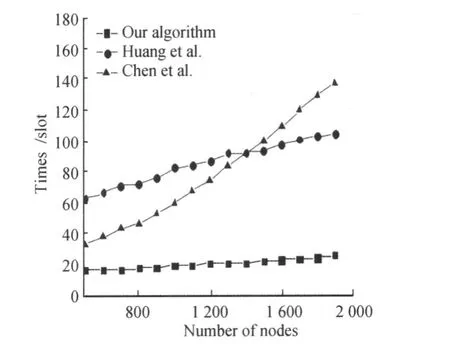
图14 节点个数变化对聚集延迟的影响Fig.14 Effect of number of nodes

如图14所示,在200 m×200 m区域内节点个数不断增加的情况下,网络半径不变,网络的最大度不断增加。本文算法的聚集延迟要比更正的Huang算法平均快2～3倍,在节点比较密时,比Chen算法要快得多,所以本文算法在节点个数变化的条件下延迟要比目前的算法要快。

接着,考察通信半径变化对数据聚集延迟的影响,下面,在 200 m×200 m区域内,随机放置2 000个节点,节点的通信半径从20 m到62 m变化,同第一个实验一样,每组30个随机图,延迟分别取30个不同的拓扑图的聚集延迟的平均值。实验结果见图15。

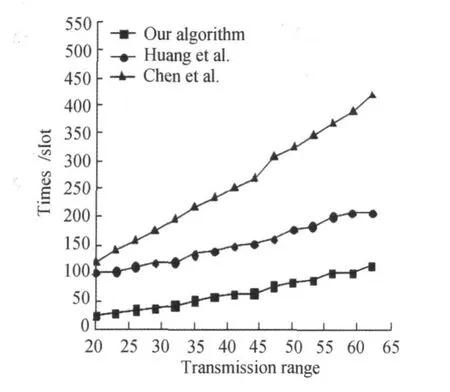
图15 通信半径变化对聚集延迟的影响Fig.15 Effect of radio range

当通信半径增加时,节点密度增加,网络的度也随着增加,网络半径减少,本文算法比Huang算法要快2倍左右,比Chen算法要快2～3倍。

单独考察网络的最大度变化对数据聚集延迟的影响。显然,在固定范围内随机布置节点,网络半径是保持不变的,当节点数不断增加,网络的度随之增加。同样,把节点随机布置在200 m×200 m范围内,节点个数不断增加,然后以网络的度最大值为基准,在每个网络度的固定值取30个图,然后延迟取平均值,实验结果见图16。实验结果与第一个实验类似。

最后本文考察网络半径变化对数据聚集延迟的影响。要保证网络半径变化,而网络的度不变,通信半径不变,那么节点个数和节点所布置的区域必须同时变化。因为是随机布置节点,所以本文可以给出一个近似公式,来表示网络半径R、网络最大度Δ、通信半径r、区域面积S(矩形区域)、节点个数n之间的关系:

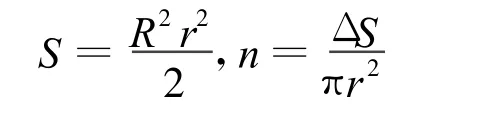
根据这个关系,本文考察当Δ=12,r=25 m, R从10～20 m变化,实验结果见图17。

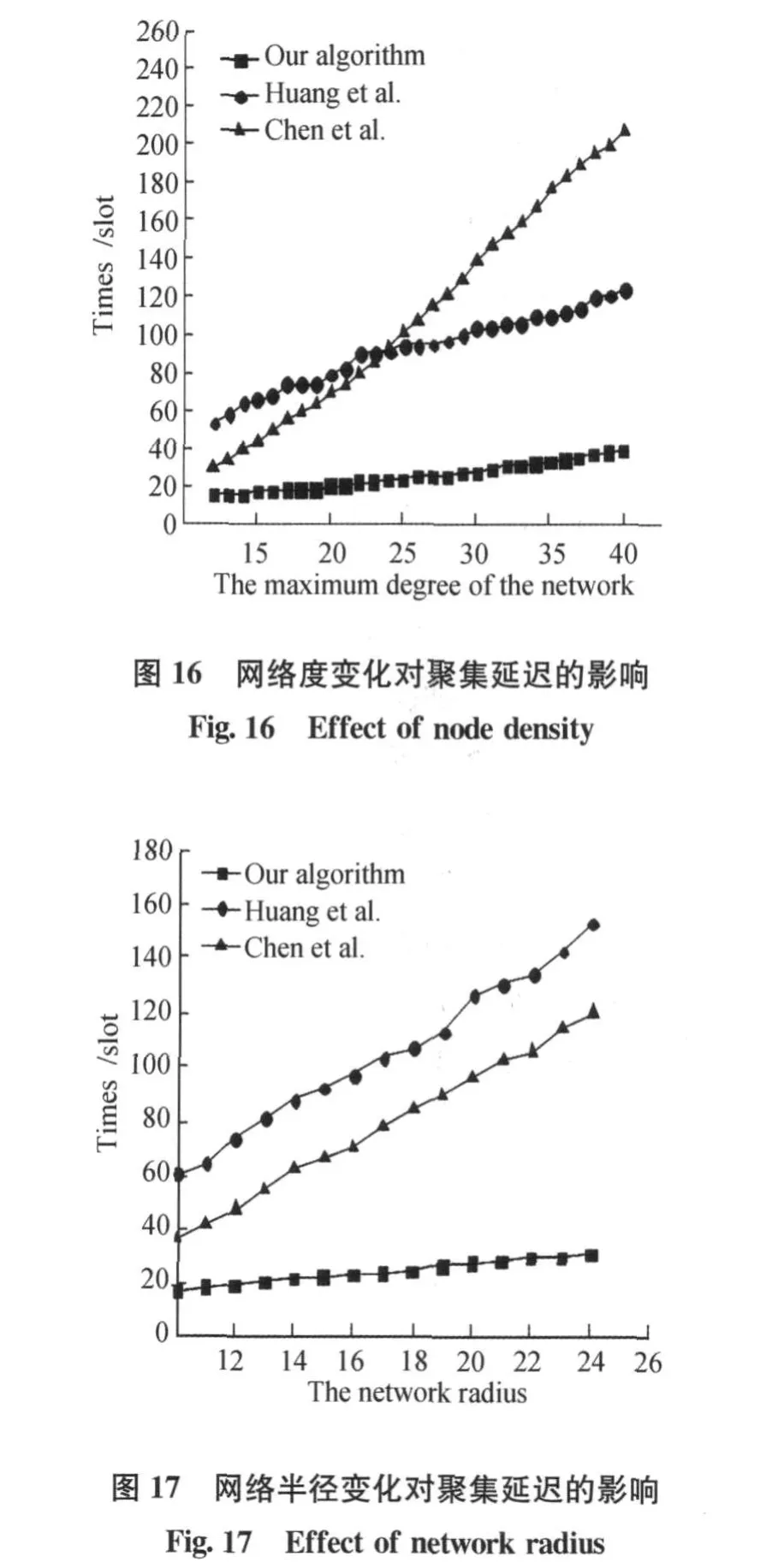
由图17可见,Chen算法和 Huang算法都趋于线性增长,因为他们的算法根据分层的思想,本文提出的算法上界是15R+Δ-15,但是一般情况下延迟远远小于这个值,这是因为对于给定的拓扑建立一棵RDAT树且采用Mini-Slot算法,将尽可能多的减少数据聚集延迟。

6 结 语

本文纠正了文献 [2]的错误,并且提出一个新的降低数据聚集延迟的调度算法,通过消减蓝点和Mini-Slot算法,给出一个近似比为16的近似算法。大大地降低了在传感器网络中数据聚集延迟,理论分析表明本文的算法的时间延迟上界为15R+Δ-15。通过实验验证了本文算法优于当前的算法。

[1]X.H.X.Chen,and J.Zhu.Minimum data aggregation time problem in wireless sensor networks[C]// Proceedings of the 1st Int' l Conference on Mobile Adhoc and Sensor Networks,Beijing,China.2005:133-142.

[2]P.-J.W.S.C.-H.Huang,C.T.Vu,Y.Li,et al.Nearly constant approximation for data aggregation scheduling in wireless sensor networks[C]//Proceedings of the IEEE INFOCOM'07,Anchorage,Alaska, USA.2007:366-372.

[3]N.Alon,A.Bar-Noy,N.Linial,et al.A lower bound for radio broadcast[J].Journal of Computer and System Sciences,1991,43(2):290-298.

[4]R.Bar-Yehuda,O.Goldreich,and A.Itai.On the time-complexity of broadcast in multi-hop radio networks:An exponential gap between determinism and randomization[J].Journal of Computer and System Sciences,1992,45(1):104-126.

[5]D.Bruschi and M.Del Pinto.Lower bounds for the broadcast problem in mobile radio networks[J].Distributed Computing,1997,10(3):129-135.

[6]I.Chlamtac and S.Kutten.On broadcasting in radio networks-problem analysis and protocol design[J]. IEEE Transactionson Communications,1985,33 (12):1 240-1 246.

[7]I.Chlamtac and O.Weinstein.The wave expansion approach to broadcasting in multihop radio networks[J]. IEEE T ransactions on Communications,1991,39(3): 426-433.

[8]M.Elkin and G.Kortsarz.Logarithmic inapproximability of the radio broadcast problem[J].Journal of Algorithms,2004,52(1):8-25.

[9]M.Elkin and G.Kortsarz.Polylogarithmic additive inapproximability of the radio broadcast problem[C]// Proceedings of The 7th Int'l Workshop on Approximation Algorithms for Combinatorial Optimization Problems-APPROX'04,Rome,Italy.2004:105-116.

[10]M.Elkin and G.Kortsarz.An improved algorithm for radio broadcast[J].Journal ACM Transactions on Algorithms,2007,3(1):810-818.

[11]I.Gaber and Y.Mansour.Centralized broadcast in multihop radio networks[J].Journal of Algorithms, 2003,46(1):1-20.

[12]R.Gandhi,S.Parthasarathy,and A.Mishra.Minimizing broadcast latency and redundancy in ad hoc networks[C]//Proceedings of ACM M obiHoc'03,Annapolis,MD,USA.2003:222-232.

[13]D.R.Kowalski and A.Pelc.Centralized deterministic broadcasting in undirected multi-hop radio networks [C]//Proceedings of the 7th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems-APPROX-RANDOM'04,Rome,Italy.2004:171-182.

[14]E.Kushilevitz and Y.M ansour.An Ω(Dlog(N/ D))lower bound for broadcast in radio networks[J]. SIAM Journal on Computing,1998,27:702-712.

[15]S.Madden,M.J.Franklin,J.M.Hellerstein,et al.Tag:a tiny aggregation service for ad-hoc sensor networks[C]//Proceedings of OSDI'02,Boston, Massachusetts,USA.2002:36-50.

[16]J.Beaver,M.A.Sharaf,A.Labrinidis,et al.Location aware routing for data aggregation for sensor networks[C]// Proceeding of Geo Sensor Networks Workshop'03,Portland,Maine.2003:1-22.

[17]C.Intanagonwiwat,D.Estrin,R.Govindan,et al. Impact of network density on data aggregation in wireless sensor networks[C]//Proceedings of the 22nd Int'l Conference on Distributed Computing Systems, Vienna,Austria.2002:1-16

[18]A.Silberstein,R.Braynard,and J.Yang.Constraint-chaining:On energy-efficient continuous monitoring in sensor networks[C]//Proceedings of SIGMOD'06,Chicago,Illinois.2006:1-12.

[19]M.Greenwald and S.Khanna.Power-conserving computation of order-statistics over sensor networks [C]//Proceedings of PODS'04,Paris,France.2004: 275-285.

[20]J.Zhao,R.Govindan,and D.Estrin.Computing aggregates for monitoring wireless sensor networks[C] //Proceedings of the First IEEE.2003 IEEE International Workshop on Sensor Network Protocols and Applications,Los Angeles,CA,USA,2003:139-148.

[21]A.Deligiannakis,V.Stoumpos,Y.Kotidis,et al. Outlier-aware data aggregation in sensor networks[C] //Proceedings of ICDE'08,Cancún,Mé xico.2008: 1 448-1 450.

[22]N.Shrivastava,C.Buragohain,D.Agrawal,et al. Medians and beyond:New aggregation techniques for sensor networks[C]//Proceedings of Sensys04,Baltimore,MD,USA.2004:239-249.

[23]J.Considine,F.Li,G.Kollios,et al.Approximate aggregation techniques for sensor databases[C]// Proceedings of ICDE'04,Boston,M A,USA.2004: 449-460.

[24]D.Chu,A.Deshpande,J.Hellerstein,et al.Approximate data collection in sensornetworks using probabilistic models[C]//Proceedings of ICDE'06, Atlanta,GA,USA.2006:48-60.

[25]A.Deshpande,C.Guestrin,W.Hong,et al.Exploiting correlated attributes in acquisitional query processing[C]//Proceedings of ICDE'05,Tokyo,Japan. 2005:143-154.

[26]B.K.Y.Yu and V.K.Prasanna.Energy-latency tradeoffs for data gathering in wireless sensor networks[C]//Proceedings of INFOCOM'04,Hong Kong,China.2004:6-18.

[27]V.Annamalai,S.K.S.Gupta,et al.On tree-based convergecasting in wireless sensor networks[C]// Proceedings of IEEE Wireless Communications and Networking-WCNC,2003,3:1 942-1 947.

[28]S.Upadhyayula,V.Annamalai,and S.K.S.Gupta.A lowlatency and energy-efficient algorithm for convergecast in wireless sensor networks[C]//Proceedings of IEEE Global Telecommunications Conference-GLOBECOM,2003:3 525-3 530.

[29]A.Kesselman and D.Kowalski.Fast distributed algorithm for convergecast in ad hoc geometric radio networks[C]//Proceedings of the 2nd Annual Conference on Wireless On-demand Network Systems and Services-WONS,2005:119-124.

[30]H.Lee and A.Keshavarzian.Towards energy-optimal and reliable data collection via collision-free scheduling in wireless sensor networks[C]//Proceedings of INFOCOM'08,Phoenix,AZ,USA.2008:2 029-2 037 .