水电站机墩结构自振特性研究
王 星,陈 婧,马震岳
(大连理工大学 建设工程学部水利工程学院,辽宁 大连 116024)
0 引 言
水轮发电机组在运行过程中难免产生振动,当振动超标时就会影响到机组的安全运行,严重时还会引发引水系统以及整个厂房的振动,甚至导致运行事故。机墩结构作为水轮发电机组的主要支撑结构,其自振特性计算和刚强度优化设计作为共振分析和动力分析的前提和基础也就变得尤为重要[1]。特别对地下厂房这一类比较复杂的结构,其自振频率的影响因素较多。而文献 [2]中对机墩自振频率的分析仅仅是将机墩组合结构简化成单自由度振动体系,利用结构力学法的自振频率计算方法[3],没有考虑组合结构的空间效应,不符合机墩的实际情况,结果必然会很粗略。不同的计算模型和不同的边界条件必然会导致自振频率的结果相差很大[4-5]。为此,着重研究不同的计算模型选取方式和范围对自振频率的影响,从而确定更能反映实际情况的计算模型,以求得到更切合实际和更加精确可靠的分析结果。
1 计算原理
机墩的动力计算复核,实际上是根据机墩由于机组振动诱发的强迫振动频率以及计算得到的机墩结构的固有振动频率,避免二者发生共振。
文献 [2]中机墩自振频率的计算过于粗略。以其中机墩垂直自振频率和水平自振频率为例,简要说明如下:
机墩垂直自振频率n01(r/min)可按下式计算:
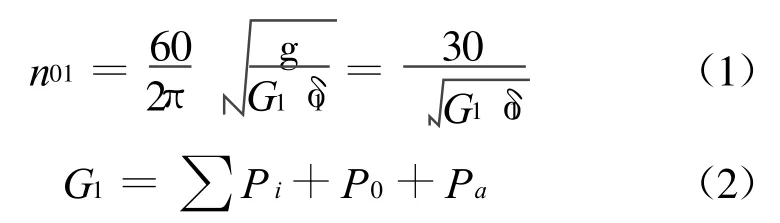
式中G1为作用于机墩上的全部垂直荷载,kN;∑Pi为机组垂直荷载(不计动力系数),kN;P0为机墩自重,kN;Pa为蜗壳顶板重,kN;δ1为单位垂直力作用下的结构垂直变位 (包括机墩压缩变位和蜗壳顶板垂直变位),m/kN。
机墩水平自振频率n02(r/min)可按下式计算:
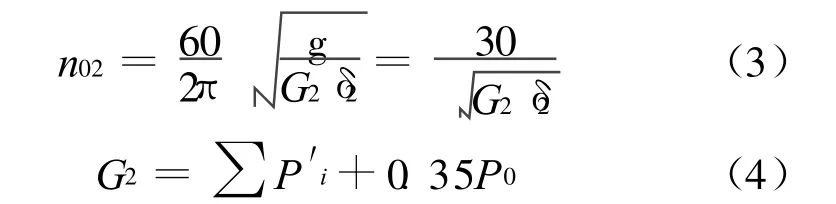
显然,上述方法根据结构动力学原理,将机墩简化成单自由度的构件,没有考虑结构的空间效应,不能完全反映板梁柱、风罩、机墩、蜗壳外围混凝土等连接结构的耦合作用和围岩的弹性支承作用等因素。同时将墩身和基础的质量全部集中到墩顶,与实际情况不完全相符。
本文利用ANSYS结构分析软件对机墩组合结构进行模态分析。模态分析是确定结构自振特性的一种动力学计算方法。多自由度体系做弹性振动时,弹性体系上受到4种力的作用:①外力{P (t)};②弹性恢复力[K]{u},[K]为结构刚度矩阵,{u}为结构位移向量;③惯性力[M]{¨u}, [M]为结构质量矩阵,{¨u}为结构加速度向量;④阻尼力 [C]{˙u},[C]为结构阻尼矩阵,{˙u}为结构速度向量。体系运动的时候,由以上4种力达到平衡,得到多自由度体系的运动方程:
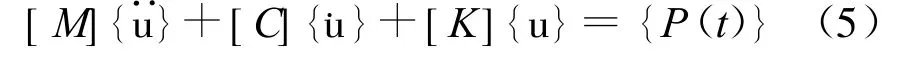
对于无阻尼自由振动体系,振动方程为:
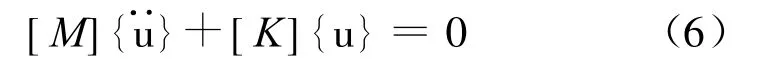
设{u(t)}=ejwtφ,代入式(6)中,得到体系特征方程:

{φ}分量不为零,故有:det|[K]-ω2[M]|=0
解出ω的n个解,即为体系的n阶自振频率。将ω的n个解回代至式(7)中,即可求出体系对应的n个自振频率的n阶振型{φ}。把全部自振频率按由小到大的顺序排列而成的向量称为频率向量ω,其中最小的频率叫做基频,振型称为第一振型,把全部振型向量按与频率对应顺序排列而成的矩阵称为振型矩阵{φ}。
2 计算模型
以某一大型水电站地下厂房为例,其1#和2#机组段连成一体,3#和4#机组段连成一体,2#和3#机组段之间以及4#机组段和安装间之间设结构缝,为简化计算,选取3#和4#机组段结构进行三维有限元计算。机墩材料为C20混凝土,其弹性模量 EC=2.55×104N/mm2,容重 γ=25 kN/mm3,泊松比μ=0.167。模型中共采用了8节点块体单元,板壳单元,三维梁单元,杆单元和弹簧单元等5种单元类型。计算模型的总体坐标系取Z轴为垂直竖向,以安装高程为原点,向上为正; X轴和Y轴为水平坐标,以机组中心为原点,X轴为纵向,正方向指向左侧;Y轴为横向,正方向指向上游侧。
为着重考虑模型的不同选取范围对机墩自振频率的影响,选取了以下6种计算模型进行对比分析。
模型1:取单个机墩作为计算对象,不考虑下部蜗壳尾水管结构及上部楼板风罩;
模型2:在模型1的基础上,机墩结构向下延伸取至尾水管锥管段为止,即包含整个蜗壳层;
模型3:在模型2的基础上,增加尾水管结构;
模型4:在模型2的基础上增加各层楼板和风罩及上下游墙;
模型5:在模型4的基础上增加尾水管等下部结构,即整个混凝土结构;
模型6:在模型5的基础上考虑洞室围岩参振情况,周围岩体每侧的计算宽度至少取2倍的厂房宽度。所有模型均为底部固定约束,围岩四周加法向弹性约束,其他边界自由。模型见图1。
3 结构固有振动特性计算
3.1 文献[2]方法
根据第1节计算方法,得出机墩结构的自振频率如下:
机墩垂直自振频率:n01=41.99 Hz
机墩水平横向自振频率:n02=26.40 Hz
3.2 模态分析方法
分别对上述6个模型进行模态分析,前10阶振动频率结果列于表1,各模型机墩第一阶垂直与水平横向自振频率列于表2。

图1 水电站厂房机墩组合结构计算模型Fig.1 Different models for the turbine foundation composite structure of powerhouse of hydropower station
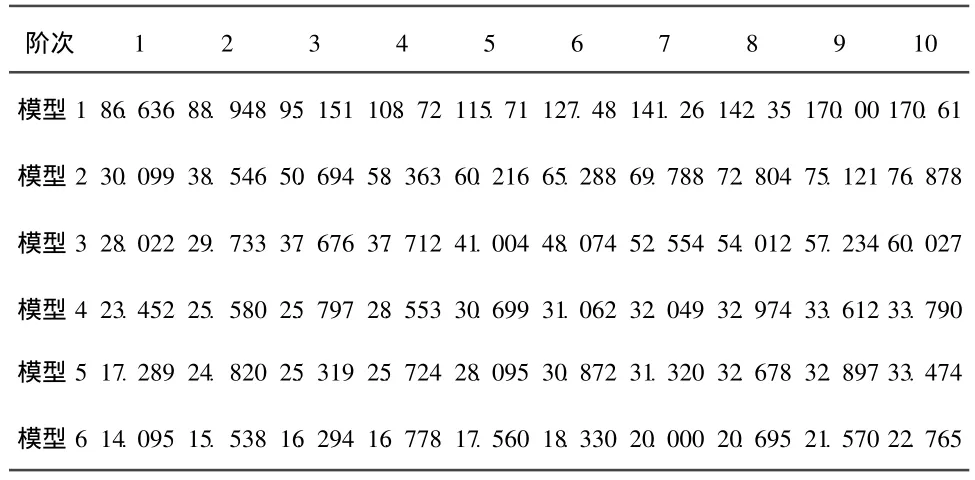
表1 各模型前10阶自振频率Table 1 First 10 natural frequencies of different models /Hz

表2 各模型机墩第一阶竖向和水平横向自振频率Table 2 First vertical and horizontal natural frequencies of turbine foundation in different models /Hz
从各模型的自振频率和振型图可以看出:
1)对于模型 1,机墩水平横向自振频率为86.636 Hz,竖向自振频率为141.26 Hz。显然由于没有考虑机墩下部混凝土结构,计算模型的高度较小,底部为固定端而没有考虑下部混凝土结构的弹性,且参振质量较小,导致机墩的自振频率要比实际高出许多,偏高的计算频率值在共振校核与动力响应分析时,将产生不利于安全评价的影响趋势。
2)相比于模型1,模型2和模型3由于参振质量的依次增加和基础弹性的考虑,自振频率呈依次减小的趋势。模型2的基本水平横向自振频率为50.694 Hz,垂直自振频率为72.804 Hz;模型3的水平横向自振频率为37.712 Hz,垂直自振频率为52.554 Hz。但从振型上看,模型3的振型多为整体振动伴随着机墩的振动,反映的振型较模型2更为全面,对结构的稳定性分析有重大意义。说明从模型范围的选取角度看,考虑尾水管更加科学。
3)根据文献 [2],计算得机墩水平自振频率为26.40 Hz,垂直自振频率为41.99 Hz,远远小于前3种模型的有限元计算所得自振频率。通过分析可知,根据规范将机墩简化成单自由度体系没有考虑到结构的空间效应,同时也降低了机墩结构的刚度,导致计算所得的频率均偏小。而单独模拟机墩部分的有限元模型1由于参振质量较小,且没有考虑到机墩底部混凝土结构的弹性影响,频率计算结果比实际又高出了许多,致使按照规范计算所得的频率相对于模型1的频率相差较大。
4)模型4,模型5,模型6在前10阶振型中均没有出现机墩的横向、扭转、垂直振动的振型,相应没有得到对应机墩横向、扭转、垂直振动的基本自振频率,其原因在于板梁柱的刚度相对机墩组合结构而言较低,其前10阶振型多为板梁柱的振动。相比于模型4,模型5和模型6依次增加了下部尾水管结构和考虑围岩的作用。从振型上看,模型5和模型6的振型更全面,整体、楼板、立柱均有相应的振动性态表现,较符合实际。
4 结 语
1)通过文献 [2]方法和有限元模态分析方法计算得出的结果进行比较分析,可以看出,规范将结构简化成单自由度体系,没有考虑结构的空间效应,不能完全反映板梁柱、风罩、机墩、蜗壳外围混凝土等组合结构的耦联效应,同时没有考虑地下厂房围岩的弹性支撑和两机一缝结构的整体效应,简化过多过粗使计算结果的可靠性降低,不能完全反映机墩结构的真实动态特性,应该采用合理的有限元模型进行计算分析。
2)本文利用有限元方法从单独模拟单个机墩开始逐渐增加其上下部分结构,直到考虑一定的围岩结构进行模态分析。从自振频率和振型的分析可知,单独模拟机墩圆筒形部分或只考虑机墩及其紧邻的上部或下部结构,都不能准确反映机墩结构的实际振动性态。模拟机墩及其组合结构的整体混凝土结构和考虑一定范围的围岩都是合理的,从理论上讲考虑一定范围的围岩结构更为科学,但从实用角度分析只模拟机墩组合机构的整体混凝土部分更为方便和直观。
3)水电站机墩组合结构形式复杂,其自振频率的影响因素较多且复杂,本文仅从模型选取范围的角度对该问题加以论证。除此之外,边界条件,楼板厚度,附加质量,孔洞及廊道,蜗壳及垫层等等都是影响机墩组合结构自振频率的重要因素,建议针对不同的情况,从实际角度出发,考虑因素和方法尽量合理全面。
[1]张 波.水电站厂房机墩组合结构振动分析[D].大连:大连理工大学,2009.
[2]SL266-2001,水电站厂房设计规范[S].北京:中国水利水电出版社,2001.
[3](美)R.W.克拉夫,J.彭津.结构动力学[M].王光远等译.北京:科学出版社,1985.
[4]姚新刚,沈振中,王孝州,等.洮河峡城水电站机墩自振特性研究 [J].人民黄河,2008,30(2):70-71.
[5]秦 亮.双排机水电站厂房支承结构动力特性研究[D].天津:天津大学,2003.

